Formule za udaljenost točke do pravca u ravnini, u smislu lp - udaljenosti, 1 ≤ p ≤ ∞.

Aleksandra Jovičić
diplomantica Odjela za matematiku,
Sveučilišta J.J.Strossmayera u Osijeku,
Trg Ljudevita Gaja 6, 31000 Osijek		 Kristian Sabo
Odjel za matematiku,
Sveučilište J.J.Strossmayera u Osijeku,
Trg Ljudevita Gaja 6, 31000 Osijek
ksabo@mathos.hr
 
Sažetak.

Formula za euklidsku udaljenost točke do pravca u ravnini dobro je poznata učenicima završnih razreda srednjih škola. U ovom radu promatramo općenitije probleme udaljenosti točke do pravca u ravnini, u smislu l_{p}-udaljenosti, 1\leq p\leq \infty. Pokazat ćemo da se i u tim slučajevima, također, mogu izvesti analogne formule za računanje udaljenosti točke do pravca.



Zahvala.

Rad je proizašao iz Diplomskog rada: “p-norme na \mathbb{R}^{n} i problemi linearne aproksimacije” autorice Aleksandre Jovičić diplomantice Sveučilišnog nastavničkog studija matematike i informatike na Odjelu za matematiku Sveučilišta J.J.Strossmayera u Osijeku.



Klučne riječi.

Funkcija udaljenosti, Udaljenost točke do pravca, l_{p}-udaljenost, Optimizacija.

1Euklidska udaljenost točke do pravca u ravnini

Ako su A=(x_{1},y_{1}) te B=(x_{2},y_{2}) dvije točke u ravnini \mathbb{R}^{2}, onda

d_{2}(A,B)=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}

zovemo euklidska udaljenost točaka A i B. Nije teško pokazati (vidi, primjerice, [3], [4]) da euklidska udaljenost zadovoljava sljedeća svojstva

\bullet [(i)] d_{2}(A,B)\geq 0 za svake dvije točke A i B iz \mathbb{R}^{2},
\bullet [(ii)] d_{2}(A,B)=0 onda i samo onda ako je A=B,
\bullet [(iii)] d_{2}(A,B)=d_{2}(B,A) za svake dvije točke A i B iz \mathbb{R}^{2},
\bullet [(iv)] d_{2}(A,C)+d_{2}(C,B)\geq d_{2}(A,B) za svake tri točke A,B i C iz \mathbb{R}^{2}.


Općenito, svaku funkciju d:\mathbb{R}^{2}\times \mathbb{R}^{2}\to[0,\infty\rangle koja ima svojstva (i)-(iv) zovemo funkcija udaljenosti na \mathbb{R}^{2} (vidi, primjerice [5]). Treba reći da se funkcija udaljenosti općenito definira na proizvoljnom nepraznom skupu, no zbog prirode našeg problema, ovdje ćemo se zadržati na skupu \mathbb{R}^{2}.

Pretpostavimo da su u pravokutnom koordinatnom sustavu zadani točka T_{0}=(x_{0},y_{0}) te pravac \pi s jednadžbom y=k\,x+l, k,l\in\mathbb{R}. Još iz srednjoškolske matematike poznato je da se euklidska udaljenost d_{2}(T_{0},\pi) točke T_{0} do pravca \pi računa po formuli

(1)
d_{2}(T_{0},\pi)=\frac{|k x_{0}+l-y_{0}|}{\sqrt{k^{2}+1}}.

Formula (1) može se izvesti na nekoliko načina primjenom geometrijskih ili algebarskih pristupa. Jedan od mogućih izvoda je svođenje na optimizacijski problem. U tu svrhu podsjetimo se kako euklidsku udaljenost d_{2}(T_{0},\pi) točke T_{0} do pravca \pi definiramo kao euklidsku udaljenost točke T_{0} i one točke na pravcu \pi koja je u smislu euklidske udaljenosti najbliža točki T_{0}. Ako je T=(x,y) proizvoljna točka na pravcu \pi, onda euklidska udaljenost točaka T i T_{0} glasi

d_{2}(T_{0},T)=\sqrt{(x-x_{0})^{2}+(y-y_{0})^{2}}=\sqrt{(x-x_{0})^{2}+(k\,x+l-y_{0})^{2}},

te je prema tome

d_{2}(T_{0},\pi)=\min_{x\in\mathbb{R}}\sqrt{(x-x_{0})^{2}+(k\,x+l-y_{0})^{2}}.

To znači da se problem svodi na minimizaciju funkcije

x\mapsto \sqrt{(x-x_{0})^{2}+(k\,x+l-y_{0})^{2}}.

Primijetimo da je umjesto prethodne funkcije dovoljno minimizirati funkciju \varphi_{2} zadanu s

\varphi_{2}(x)=(x-x_{0})^{2}+(k\,x+l-y_{0})^{2}.

Kako je \varphi_{2} kvadratna funkcija, njezin globalni minimum se postiže u apscisi tjemena odgovarajuće parabole, koju ćemo označiti s \xi_{2} te je

\xi_{2}=\frac{k\,y_{0}+x_{0}-k\,l}{k^{2}+1},

odakle iz d_{2}(T_{0},\pi)=\sqrt{\varphi_{2}(\xi_{2})}, nakon kraćeg računa dobivamo da je



 d_{2}(T_{0},\pi)=\displaystyle\frac{|k\,x_{0}+l-y_{0}|}{\sqrt{k^{2}+1}}.
 


 

Točku (\xi_{2}, k\,\xi_{2}+l) na pravcu \pi koja je u smislu euklidske udaljenosti najbliža točki T_{0} zovemo ortogonalna projekcija točke T_{0} na pravac \pi. Ortogonalna projekcija točke na pravac u ovom je slučaju, očigledno, jedinstvena.

Osim euklidske udaljenosti, moguće je, također, analizirati problem određivanja udaljenosti točke do pravca i u smislu nekih drugih funkcija udaljenosti. U ovom radu promatramo jednu klasu funkcija udaljenosti koje su poznate kao l_{p}-udaljenosti, 1\leq p\leq\infty. Spomenimo da je euklidska udaljenost specijalni slučaj l_{p}-udaljenosti za p=2. Pokazat ćemo da se za svaku od l_{p}-udaljenosti, 1\leq p\leq\infty, također, mogu izvesti lijepe zatvorene formule za udaljenost točke do pravca. Tehnike koje ćemo pri tome koristiti zahtijevaju samo poznavanje osnovnih tvrdnji Diferencijalnog računa funkcije jedne varijable. Kao motivacija za pripremu ovog rada poslužio je članak [2] u kojem se promatra opći slučaj l_{p}-udaljenosti, 1\leq p\leq\infty točke do hiperravnine u \mathbb{R}^{n}.

2l_{p}-udaljenosti, 1\leq p\leq\infty

Ako su A=(x_{1},y_{1}) i B=(x_{2},y_{2}), onda {l_{p}-udaljenost, 1\leq p\leq \infty,} točaka A i B definiramo na sljedeći način

d_{p}(A,B)=\left\lbrace \begin{array}{ll} \left(|x_{1}-x_{2}|^{p}+|y_{1}-y_{2}|^{p}\right)^{1/p},&1\leq p\lt \infty,\\ \max\lbrace |x_{1}-x_{2}|,|y_{1}-y_{2}|\rbrace ,&p=\infty. \end{array}\right.

Primijetimo da za p=2 dobivamo euklidsku udaljenost. Može se pokazati da svaka od l_{p}-udaljenosti, 1\leq p\leq\infty, zadovoljava uvjete (i)-(iv) iz prvog odjeljka te su one, sukladno tome, funkcije udaljenosti (vidi [4]).

Potpuno analogno kao i u slučaju euklidske udaljenosti, l_{p}-udaljenost d_{p}(T_{0},\pi) točke T_{0} do pravca \pi definiramo na sljedeći način

d_{p}(T_{0},\pi)=\min_{x\in\mathbb{R}}\left(|k x+l-y_{0}|^{p}+|x-x_{0}|^{p}\right)^{1/p},\quad 1\leq p\lt \infty,

te

d_{\infty}(T_{0},\pi)=\min_{x\in\mathbb{R}}\max\lbrace |k x+l-y_{0}|,|x-x_{0}|\rbrace .

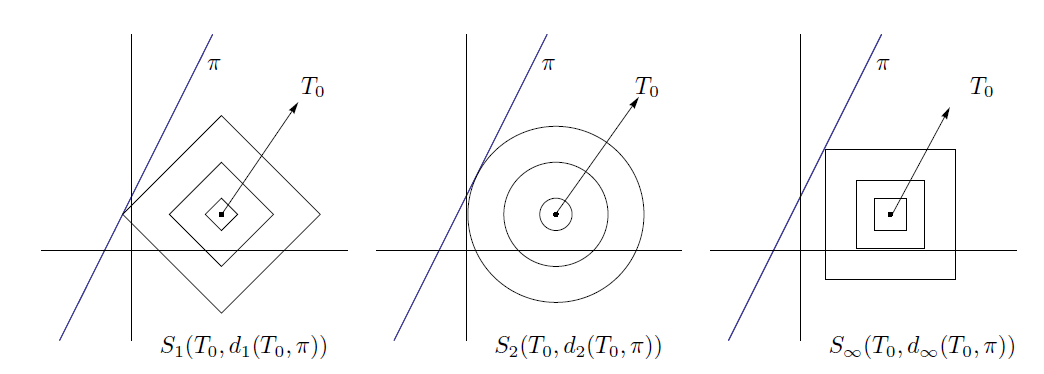
Gledano geometrijski, udaljenost točke T_{0} do pravca \pi možemo interpretirati na sljedeći način. Pretpostavimo da smo nacrtali {l_{p}-kružnicu}, 1\leq p \leq \infty (vidi primjerice [1]):

S_{p}(T_{0},\varepsilon)=\lbrace T\in\mathbb{R}^{2}:d_{p}(T,T_{0})=\varepsilon\rbrace ,

sa središtem u točki T_{0} malenog polumjera \varepsilon\gt 0. Napuhujemo li kružnicu S_{p}(T_{0},\varepsilon), 1\leq p\leq \infty, ona će u jednom trenutku za neki \varepsilon_{p}\gt 0 dotaknuti pravac \pi. Polumjer tako dobivene kružnice S_{p}(T_{0},\varepsilon_{p}), 1\leq p\leq \infty, očigledno predstavlja l_{p}- udaljenost točke T_{0} do pravca \pi (vidi Sliku 1). Pri tome točku (\xi_{p},\eta_{p}) na pravcu \pi koja je u smislu l_{p}-udaljenosti najbliža točki T_{0} zovemo {l_{p}-projekcija} točke T_{0} na pravac \pi. Sa Slike 1 odmah je jasno da l_{1} i l_{\infty}-projekcije točke na pravac općenito nisu jedinstvene. Spomenimo da su za sve ostale p, 1\lt p\lt \infty, pripadne l_{p}-projekcije jedinstvene.

Slika 1: Točka T_{0}, pravac \pi i kružnice S_{p}(T_{0},\varepsilon),\,p=1,2,\infty


3l_{1}-udaljenost točke do pravca

Iz tehničkih razloga u ovom odjeljku posebno ćemo izvesti formulu za slučaj l_{1}-udaljenosti. Neka su, kao i dosada, zadani točka T_{0}=(x_{0},y_{0}) te pravac y=k\,x+l. Pri tome u izvodu razlikujemo dvije različite mogućnosti: k=0 te k\neq 0.

Ako je k=0, onda funkcija x\mapsto |l-y_{0}|+|x-x_{0}| postiže globalni minimum u točki x=x_{0}, te je

(2)
d_{1}(T_{0},\pi)=|l-y_{0}|.

Pretpostavimo da je k\neq 0. Funkcija

(3)
x\mapsto |k x+l-y_{0}|+|x-x_{0}|,

je omeđena odozdo te je

\lim_{x\to\infty} \left(|k x+l-y_{0}|+|x-x_{0}|\right)=\lim_{x\to-\infty}\left( |k x+l-y_{0}|+|x-x_{0}|\right)=\infty,

pa postoji točka iz \mathbb{R} u kojoj se postiže njezin globalni minimum. Nadalje, funkcija (3) je po dijelovima linearna te nije derivabilna u točkama \frac{y_{0}-l}{k} i x_{0} te se globalni minimum funkcije (3) postiže u jednoj od tih dviju točaka.

Očigledno je

(4)
\begin{eqnarray} d_{1}(T_{0},\pi)&=&\min\left\lbrace |k x_{0}+l-y_{0}|,\left|\frac{y_{0}-l}{k}-x_{0}\right|\right\rbrace \\ \nonumber &=&\min\left\lbrace |k x_{0}+l-y_{0}|,\frac{|k x_{0}+l-y_{0}|}{|k|}\right\rbrace \\ &=& \frac{|k x_{0}+l-y_{0}|}{\max\lbrace |k|,1\rbrace }.\end{eqnarray}

Konačno iz formula (2) i (4) dobivamo da je





 d_{1}(T_{0},\pi)=\displaystyle\frac{|k x_{0}+l-y_{0}|}{\max\lbrace |k|,1\rbrace }.
 


 

Označimo s (\xi_{1},\eta_{1})l_{1}-projekciju točke T_{0} na pravac \pi. Uočimo da se za |k|\gt 1 minimum funkcije (3) postiže u x=\frac{y_{0}-l}{k}, dok se za |k|\lt 1 minimum funkcije (3) postiže u x=x_{0}.

Očito je

(5)
\xi_{1}=\left\lbrace \begin{array}{ll}\frac{y_{0}-l}{k},& |k|\gt 1,\\ x_{0},& |k|\lt 1,\end{array}\right.,\quad \eta_{1}=k\,\xi_{1}+l=\left\lbrace \begin{array}{ll}y_{0},& |k|\gt 1,\\ k\,x_{0}+l,& |k|\lt 1.\end{array}\right.

Pokažimo da se u slučaju |k|=1 minimum funkcije (3) postiže u bilo kojoj konveksnoj kombinaciji brojeva \frac{y_{0}-l}{k} i x_{0}, tj. za svaki

(6)
\xi_{1}(\lambda)=\lambda \frac{y_{0}-l}{k}+(1-\lambda) x_{0},\quad \lambda\in [0,1].

Zaista, za |k|=1 te \lambda\in[0,1] imamo

\begin{eqnarray} \left|k\,\xi_{1}(\lambda)+l-y_{0}\right|+\left|\xi_{1}(\lambda)-x_{0}\right|&=&\left|k \left(\lambda \frac{y_{0}-l}{k}+(1-\lambda) x_{0}\right)+l-y_{0}\right|\\ &+&\left|\lambda \frac{y_{0}-l}{k}+(1-\lambda) x_{0}-x_{0}\right|\\ \nonumber &=&(1-\lambda)|k x_{0}+l-y_{0}|+\lambda |k x_{0}+l-y_{0}|\\ \nonumber &=& |k x_{0}-l-y_{0}|\\ \nonumber &=& d_{1}(T_{0},\pi).\end{eqnarray}

Zaključujemo kako je u slučaju |k|\neq 1, l_{1}-projekcija točke T_{0} na pravac \pi jedinstvena točka (\xi_{1},\eta_{1}) zadana s (5), dok je u slučaju |k|=1 svaka točka oblika (\xi_{1}(\lambda),k\,\xi_{1}(\lambda)+l-y_{0}), \lambda\in[0,1], l_{1}-projekcija točke T_{0} na pravac \pi, pri čemu je \xi_{1}(\lambda) zadan sa (6).

4l_{p}-udaljenost, 1\lt p\lt \infty, točke do pravca

U ovom općem slučaju problem se svodi na minimizaciju funkcije

x\mapsto \left(|k x+l-y_{0}|^{p}+|x-x_{0}|^{p}\right)^{1/p},\quad 1\lt p\lt \infty.

Slično kao kod euklidske udaljenosti dovoljno je minimizirati funkciju

\varphi_{p}(x)=|k x+l-y_{0}|^{p}+|x-x_{0}|^{p}, \quad 1\lt p\lt \infty.

Kako je funkcija \varphi_{p} omeđena odozdo te je

\lim_{x\to\infty}\left( |k x+l-y_{0}|^{p}+|x-x_{0}|^{p}\right)=\lim_{x\to-\infty}\left( |k x+l-y_{0}|^{p}+|x-x_{0}|^{p} \right)=\infty,

postoji točka iz \mathbb{R} u kojoj se postiže njezin globalni minimum. S ciljem određivanja te točke, posebno promatramo dva slučaja: k=0 te k\neq 0.

Ako je k=0, onda je \varphi_{p}(x)=|l-y_{0}|^{p}+|x-x_{0}|^{p}, te se njezin minimum postiže u točki x=x_{0} pa je

(7)
d_{p}(T_{0},\pi)=|l-y_{0}|.

Neka je k\neq 0. Primijetimo da je funkcija \varphi_{p} derivabilna u svim točkama na \mathbb{R} osim možda u točkama x=x_{0} te x=\frac{y_{0}-l}{k} te ćemo u svrhu minimizacije funkcije \varphi_{p} upotrijebiti znanja iz Diferencijalnog računa funkcije jedne varijable.

Promatrajmo funkciju \varphi_{p} na skupu \mathbb{R}\setminus\left\lbrace x_{0},\frac{y_{0}-l}{k}\right\rbrace. Bez smanjenja općenitosti pretpostavimo da je x_{0}\lt \frac{y_{0}-l}{k} (slučaj x_{0}\geq \frac{y_{0}-l}{k} može se analizirati potpuno analogno).

Pokažimo najprije da funkcija \varphi_{p} nema stacionarnih točaka na intervalima \langle -\infty,x_{0}\rangle te \langle \frac{y_{0}-l}{k},+\infty\rangle.

Ako je x\in\langle -\infty, x_{0}\rangle, funkcija \varphi_{p} je derivabilna u x te je

\begin{eqnarray} \frac{d\varphi_{p}(x)}{dx}&=&|k|^{p} p\left|x-\frac{y_{0}-l}{k}\right|^{p-1}\text{sign}\left(x-\frac{y_{0}-l}{k}\right)+p |x-x_{0}|^{p-1}\text{sign}(x-x_{0})\\ \nonumber &=&-|k|^{p} p\left|x-\frac{y_{0}-l}{k}\right|^{p-1}-p |x-x_{0}|^{p-1}\lt 0,\end{eqnarray}

gdje je \text{sign}(x)=\left\lbrace \begin{array}{rl} 1,& x\gt 0\\ 0,& x=0\\ -1,&x\lt 0, \end{array}\right. tzv. funkcija predznaka.

Ako je x\in\langle \frac{y_{0}-l}{k},+\infty\rangle, funkcija \varphi_{p} je derivabilna u x te je

\begin{eqnarray} \frac{d\varphi_{p}(x)}{dx}&=&|k|^{p} p\left|x-\frac{y_{0}-l}{k}\right|^{p-1}+p |x-x_{0}|^{p-1}\gt 0.\end{eqnarray}

Preostaje analizirati slučaj x\in\langle x_{0},\frac{y_{0}-l}{k}\rangle. Na tom je skupu funkcija \varphi_{p} također derivabilna te je

(8)
\begin{eqnarray} \frac{d\varphi_{p}(x)}{dx}&=&-|k|^{p} p\left|x-\frac{y_{0}-l}{k}\right|^{p-1}+p |x-x_{0}|^{p-1}.\end{eqnarray}

Rješenje jednadžbe \frac{d\varphi_{p}(x)}{dx}=0, glasi

(9)
\xi_{p}=\frac{1}{|k|^{\frac{p}{p-1}}+1}x_{0}+\frac{|k|^{\frac{p}{p-1}}}{|k|^{\frac{p}{p-1}}+1}\frac{y_{0}-l}{k}.

Uočimo da je \xi_{p}\in\langle x_{0},\frac{y_{0}-l}{k}\rangle te

\varphi_{p}(\xi_{p})=\left(\displaystyle\frac{|k x_{0}+l-y_{0}|}{\left(|k|^{\frac{p}{p-1}}+1\right)^{\frac{p-1}{p}}}\right)^{p}.

Kandidati za točku u kojoj se postiže globalni minimum funkcije \varphi_{p} su x_{0}, \frac{y_{0}-l}{k} te \xi_{p} zadana s (9). Pokažimo da je

\min\left\lbrace \varphi_{p}(x_{0}),\varphi_{p}\left(\frac{y_{0}-l}{k}\right),\varphi_{p}(\xi_{p})\right\rbrace =\varphi_{p}(\xi_{p}).

U tu svrhu uočimo da za svaki 1\lt p\lt \infty i svaki k\in\mathbb{R} vrijedi

(10)
\left(|k|^{\frac{p}{p-1}}+1\right)^{\frac{p-1}{p}}\gt |k|,

te

(11)
\left(|k|^{\frac{p}{p-1}}+1\right)^{\frac{p-1}{p}}\gt 1.

Prema (10) i (11) imamo

\min\left\lbrace \left(\frac{|k x_{0}+l-y_{0}|}{|k|}\right)^{p},\left|k x_{0}+l-y_{0}\right|^{p},\left(\frac{|k x_{0}+l-y_{0}|}{\left(|k|^{\frac{p}{p-1}}+1\right)^{\frac{p-1}{p}}}\right)^{p}\right\rbrace =\left(\frac{|k x_{0}+l-y_{0}|}{\left(|k|^{\frac{p}{p-1}}+1\right)^{\frac{p-1}{p}}}\right)^{p}.

Konačno slijedi da je d_{p}(T_{0},\pi)=\left(\varphi(\xi_{p})\right)^{1/p}, odakle je



 d_{p}(T_{0},\pi)=\displaystyle\frac{|k x_{0}+l-y_{0}|}{\left(|k|^{\frac{p}{p-1}}+1\right)^{\frac{p-1}{p}}},\quad 1\lt p\lt \infty.
 

Tablica 1:


Iz izvoda formule (1) neposredno proizlazi da je (\xi_{p},k\,\xi_{p}+l), gdje je \xi_{p} dan s (9) pripadna l_{p}-projekcija točke T_{0} na pravac \pi.

Ako s q\in \mathbb{R} označimo tzv. konjugirani eksponent od p (vidi [3]), odnosno broj sa svojstvom da je \frac{1}{p}+\frac{1}{q}=1, onda formulu (1) možemo zapisati u obliku

d_{p}(T_{0},\pi)=\frac{|k x_{0}+l-y_{0}|}{\left(|k|^{q}+1\right)^{\frac{1}{q}}}= \frac{|k x_{0}+l-y_{0}|}{d_{q}((k,1),(0,0))}.


5l_{\infty}-udaljenost točke do pravca

Ako su T_{0}=(x_{0},y_{0}) te y=k\,x+l, onda je problem određivanja l_{\infty}-udaljenosti ekvivalentan minimizaciji funkcije

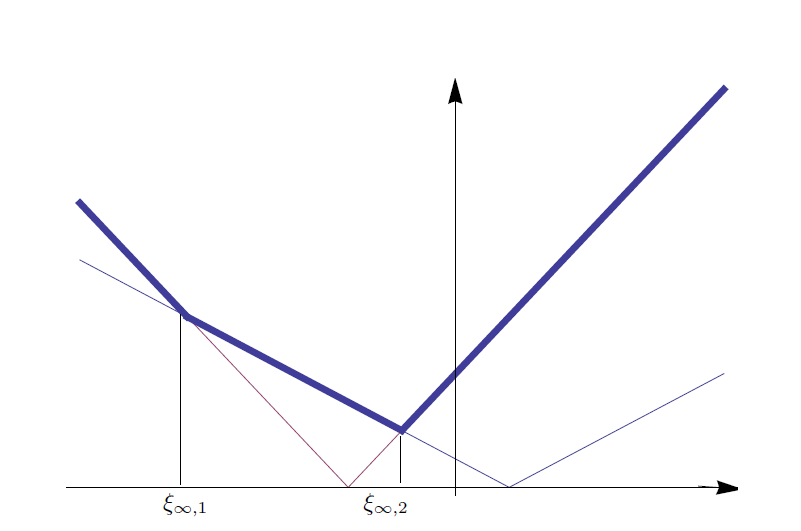
\varphi_{\infty}(x)= \max\lbrace |x-x_{0}|,|k\,x+l-y_{0}|\rbrace .

Analogno kao u slučaju funkcije \phi_{p} može se pokazati da postoji točka u kojoj se postiže globalni minimum funkcije \varphi_{\infty}. Funkcija \varphi_{\infty} je konveksna po dijelovima linearna funkcija te iz grafa (vidi Sliku 2) slijedi da se njezin globalni minimum postiže u točki \xi_{\infty} za koju vrijedi

 

Slika 2: Graf funkcije \phi_\infty za k\ne0.
|\xi_{\infty}-x_{0}|=|k\,\xi_{\infty}+l-y_{0}|.

Ako je |k|\neq 1, ova jednadžba ima dva rješenja

\xi_{\infty,1}=\frac{y_{0}-x_{0}-l}{k-1},\quad \xi_{\infty,2}=\frac{y_{0}-x0-l}{k+1}

te je

\begin{align*} \min \varphi_{\infty}(x)&= \min \lbrace \varphi_{\infty}(\xi_{\infty,1}),\varphi_{\infty}(\xi_{\infty,2})\rbrace \\ &=\min\left\lbrace \frac{|kx_{0}+l-y_{0}|}{|k-1|},\frac{|kx_{0}+l-y_{0}|}{|k+1|}\right\rbrace \\ &=|kx_{0}+l-y_{0}|\min\left\lbrace \frac{1}{|k-1|},\frac{1}{|k+1|}\right\rbrace =\frac{|kx_{0}+l-y_{0}|}{|k|+1}, \end{align*}

pri čemu je posljednja jednakost posljedica identiteta

\min\left\lbrace \frac{1}{|k-1|},\frac{1}{|k+1|}\right\rbrace =\frac{1}{|k|+1},

koji se može lako provjeriti. Slično se može analizirati slučaj |k|=1, te konačno dobivamo formulu



 d_{\infty}(T_{0},\pi)=\displaystyle\frac{|k\,x_{0}+l-y_{0}|}{|k|+1}.
 

Primijetimo, također, da je

d_{\infty}(T_{0},\pi)=\frac{|k\,x_{0}+l-y_{0}|}{d_{1}((k,1),(0,0))}.

Izvod formule za l_{\infty}-projekciju točke T_{0} na pravac \pi ostavljamo zainteresiranim čitateljima.

6Zaključna formula

Na kraju ćemo rezimirati sve prethodno navedene formule. Ako su p,q\in\mathbb{R} konjugirani eksponenti, odnosno, takvi da je \frac{1}{p}+\frac{1}{q}=1 te ako je konjugirani eksponent od p=1 definiramo uobičajeno kao q=\infty, onda l_{p}-udaljenost 1\leq p\leq \infty, d_{p}(T_{0},\pi) točke T_{0} do pravca \pi glasi



 d_{p}(T_{0},\pi)=\displaystyle\frac{|k\,x_{0}+l-y_{0}|}{d_{q}((k,1),(0,0))}.
 


Također, osim u eksplicitnom obliku, pravac \pi možemo promatrati u implicitnom obliku ax+by+c=0. U tom se slučaju može izvesti odgovarajuća formula za udaljenost točke T_{0} do pravca \pi, koja glasi



 d_{p}(T_{0},\pi)=\displaystyle\frac{|a\,x_{0}+b\,y_{0}+c|}{d_{q}((a,b),(0,0))},
 

gdje su p,q\in\mathbb{R} konjugirani eksponenti.

Bibliografija
[1] Lj. Arambašić, I. Zavišić, p-norme na \mathbb{R}^{2}, kružnice S_{p} i brojevi \pi_{p}, Osječki matematički list, 10(2010), 131-138
[2] E. Melachrinoudis, An Analytical Solution to the Minimum L_{p}-Norm of a Hyperplane}, Journal of Mathematical Analysis and Applications 211(1997), 172-189
[3] S. Kurepa, Funkcionalna analiza : elementi teorije operatora, Školska knjiga, Zagreb, 1981.
[4] S. Mardešić, Matematička analiza, 1. dio, Školska knjiga, Zagreb, 1974.
[5] Š. Ungar, Matematička analiza u \mathbb{R}^{n}, Golden Marketing - Tehnička knjiga, Zagreb, 2005.

 

Share this