P	U	S	Č	P	S	N
				1	2	3
4	5	6	7	8	9	10
11	12	13	14	15	16	17
18	19	20	21	22	23	24
25	26	27	28	29	30	31

optimizacija

Prepoznavanje lica pomoću tenzorske dekompozicije singularnih vrijednosti

Ivan Zirdum i Nela Bosner

Moderna tehnologija i stalan porast broja stanovnika na Zemlji razlog su velike produkcije podataka. Svaki dan se proizvede ogromna količina novih podataka koje je potrebno spremati, obraditi, a često i slati. Zbog toga je bilo potrebno osmisliti načine za efikasno spremanje podataka kako bi oni zauzimali što je manje moguće prostora, a da glavna informacija bude očuvana. Lijep primjer toga je kompresija digitalne slike. Uzmimo za primjer sliku dimenzije 3000 \times 2000 piksela. Kako bismo takvu sliku spremili u memoriju potrebno nam je 3000 \cdot 2000 \cdot 24 = 144000000 bitova memorije (za pamćenje jednog piksela koristimo 24 bita) što iznosi 18 megabajta.

U ovom članku bavit ćemo se matričnom (tenzorskom) dekompozicijom koja nam omogućava da iz nekog skupa podataka, prikazanog pomoću matrice (tenzora), izdvojimo "najvažniji" dio, a ostatak izostavimo. Koristeći tu tehniku možemo komprimirati slike, razviti algoritme koji: klasificiraju rukom pisane znamenke, prepoznaju ljudska lica i još mnogo toga. Zamislite sada da ste zaposleni u pošti i da je vaša zadaća sortirati pristigla pisma prema poštanskom broju kako bi ona stigla na pravu adresu. Možda biste radije bili prometni policajac na autocesti koji je zadužen za praćenje brzine automobila koje ulaze u tunel. Vaš posao je snimiti tablice automobila koji ne poštuju ograničenje brzine, a zatim u bazi podataka registracija vozila pronaći tu tablicu te na priloženu adresu vlasnika poslati kaznu za prebrzu vožnju. Biste li svaki dan isti posao radili ručno ili biste radije pokušali taj postupak automatizirati? Srećom, ljudi su se već susreli s ovim problemom i smislili mnogo načina kako taj posao ubrzati i uštediti dragocjeno vrijeme. Svi navedeni problemi mogu se riješiti upotrebom jednog moćnog alata numeričke matematike koji ćemo vam pokušati približiti u ostatku ovog članka.

1Matrična dekompozicija singularnih vrijednosti (SVD)

Jedna od najkorisnijih dekompozicija i s teorijske strane (za dokazivanje) i s praktične strane, je dekompozicija singularnih vrijednosti (engl. singular value decomposition) ili, skraćeno, SVD. Sljedeći teorem pokazuje da za svaku matricu postoji takva dekompozicija.

Teorem 1. (SVD) Neka su m i nn \geq m prirodni brojevi te A proizvoljna n \times m realna matrica. Tada postoji dekompozicija

(1)

A = U\Sigma V^{T},

gdje su U \in \mathbb{R}^{n \times n} i V \in \mathbb{R}^{m \times m} ortogonalne matrice, a \Sigma \in \mathbb{R}^{n \times m} dijagonalna matrica,

\Sigma = diag( \sigma_{1}, \sigma_{2}, \cdots,\sigma_{m}),

\sigma_{1} \geq \sigma_{2} \geq \cdots \geq \sigma_{m} \geq 0 .

Ilustrirajmo SVD:

Slika 1: A\in \mathbb{R}^{n\times m}, U\in \mathbb{R}^{n\times n}, \Sigma \in \mathbb{R}^{n \times m}, V^{T} \in \mathbb{R}^{m \times m}.

Ako U zapišemo kao U=(U_{m}\,U_{m}^{\perp}), gdje je U_{m} \in \mathbb{R}^{n \times m}, a \Sigma zapišemo kao \begin{pmatrix} \Sigma_{m} \\ 0 \end{pmatrix} gdje je \Sigma_{m} \in \mathbb{R}^{m\times m}, tada dobijemo tanki SVD.

A=U_{m} \Sigma_{m} V^{T},

Ilustirajmo sada tanki SVD:

Slika 2: A\in \mathbb{R}^{n\times m}, U_{m}\in \mathbb{R}^{n\times m}, \Sigma_{m} \in \mathbb{R}^{m \times m}, V^{T} \in \mathbb{R}^{m \times m}.

Jako važnu primjenu SVD-a daje sljedeći teorem.

Teorem 2. Neka je A = U_{m}\Sigma_{m} V^{T} dekompozicija singularnih vrijednosti (SVD) realne matrice A tipa n \times m, n \geq m. Zapišimo matrice U_{m} i V iz SVD-a od A u stupčanom obliku

U_{m} = (u_{1}, \cdots, u_{m}), \hspace{5mm} V = (v_{1}, \cdots, v_{m}).

Onda matricu A možemo pisati kao zbroj matrica ranga 1

A= U_{m} \Sigma_{m} V^{T} = \sum_{i=1}^{m} \sigma_{i} u_{i} v_{i}^{T}.

Matricu A_{k}, istog tipa kao i A, ranga rang(A_{k}) \leq k \lt m, koja je po 2-normi najbliža matrici A, možemo zapisati kao

A_{k} = U_{m} \Sigma_{k} V^{T} = \sum_{i=1}^{k} \sigma_{i} u_{i} v_{i}^{T}

pri čemu je

\Sigma_{k} = diag(\sigma_{1}, \cdots , \sigma_{k}, 0, \cdots, 0).

Pritom je

||A-A_{k}||_{2} = \sigma_{k+1}

najmanja udaljenost između A i svih matrica ranga najviše k.

1.1Primjena dekompozicije matrice singularnih vrijednosti

Jedna od primjena prethodnog teorema je kompresija slika. Neka je dana n \times m matrica A s elementima a_{i,j} \in [0,1]. Zamislimo da A predstavlja n \times m grayscale (crno-bijelu) sliku, gdje broj na (i,j) mjestu u matrici predstavlja intenzitet svjetlosti piksela na mjestu (i,j) na slici. Ako uzmemo da vrijednost nula predstavlja crno, a jedan bijelo, zanimljivo je pitanje što će se dogoditi kad napravimo A = U \Sigma V^{T}, a onda u matrici \Sigma posljednjih nekoliko ne-nul elemenata stavimo na nulu te promotrimo dobivenu sliku A_{k}, gdje je A_{k} = U \Sigma _{k} V^{T} = \sum_{i=1}^{k} \sigma_{i} u_{i} v_{i}^{T}, a \Sigma_{k} = diag(\sigma_{1}, \cdots, \sigma_{k}, 0, \cdots, 0).

Slika 3: Testna slika A dimenzije 376\times 350 u JPG formatu zauzima 129 kb.

Preciznije, neka je A = U \Sigma V^{T}, SVD matrice A. Prema teoremu 2 , vrijedi da je A_{k} = \sum_{i=1}^{k} \sigma_{i} u_{i} v_{i}^{T} najbolja aproksimacija matrice A matricom ranga k, u smislu ||A-A_{k}|| = \sigma_{k+1}. Da bismo spremili podatke u_{1}, \cdots , u_{k} te \sigma_{1}v_{1}, \cdots, \sigma_{k}v_{k} iz kojih možemo dobiti matricu A_{k} potrebno je pamtiti samo (m+n)\cdot k brojeva budući da su u_{i} i v_{i} vektori iz \mathbb{R}^{m} odnosno iz \mathbb{R}^{n}. S druge strane, za spremanje matrice A potrebno je pamtiti svih m \cdot n brojeva. Stoga, koristimo A_{k} kao kompresiju slike A.

Slika 4: Kompresija A_{k} s a) k=50, b) k=25, c) k=15, a zauzimaju redom 35 kb, 18 kb te 11 kb.

2Tenzori

Do sada smo razmatrali linearnu algebru, gdje su glavni objekti vektori i matrice. Njih možemo smatrati kao jednodimenzionalna i dvodimenzionalna polja podataka. Tenzor je višedimenzionalni ekvivalent vektora i matrice i možemo ga predstaviti višedimenzionalnim poljem brojeva. Red tenzora jednak je broju indeksa potrebnih za indeksiranje njegovih elemenata. Primjerice, skalar možemo smatrati tenzorom reda 0, vektor tenzorom reda 1, a matricu tenzorom reda 2. Tenzori reda većeg ili jednakog 3 nazivaju se tenzorima višeg reda. Preciznije, tenzor reda N je element tenzorskog produkta N vektorskih prostora.

Red tenzora \mathcal{A} \in \mathbb{R}^{I_{1} \times I_{2} \times \dots \times I_{N}} je N. Elemente od \mathcal{A} označavamo s \mathcal{A}_{i_{1} i_{2} \dots i_{n}}, gdje su 1 \leq i_{n} \leq I_{n}, n = 1,2, \dots N.

Svaki indeks u tenzoru nazivamo mod, a dimenzija pripadnog moda je broj različitih vrijednosti koje taj indeks može poprimiti. Unutar tenzora možemo indeksirati podtenzore ograničavanjem pojedinih indeksa. Primjerice, za tenzor \mathcal{A} = (a_{i_{1} i_{2} i_{3}}) \in \mathbb{R}^{I_{1} \times I_{2} \times I_{3}} reda 3 možemo fiksiranjem indeksa u modu 1,2 ili 3 definirati podtenzore kao \mathcal{A}_{i_{1} = n} = \mathcal{A}_{n::},\mathcal{A}_{i_{2} = n} = \mathcal{A}_{:n:} ili \mathcal{A}_{i_{3} = n} = \mathcal{A}_{::n}.
Primjetimo da su u tom slučaju dva indeksa slobodna pa su podtenzori zapravo novi tenzori reda 2, odnosno matrice. Posebno za slučaj tenzora reda 3 te podtenzore nazivamo horizontalnim, lateralnim i frontalnim odsječcima. Također možemo definirati i vektore po modu n na način da fiksiramo sve indekse osim jednoga, npr. vektor u modu 1 se dobije kao \mathcal{A}_{:i_{2} i_{3}}. Analogno za tenzor reda N možemo definirati podtenzore reda manjeg ili jednakog N. Na sljedećoj slici su prikazani primjeri podtenzora za tenzor reda 3.

Slika 5: Primjeri podtenzora. Vektori tenzora u: modu 1, modu 2 i modu 3.

Slika 6: Primjeri podtenzora. Horizontalni, lateralni i frontalni odsječci.

MATLAB kod

function Av=vekt_tenz_mod(A,tmod,j,k)
% Av=vekt_tenz_mod(A,mod,i1,i2) vraca vektor tenzora A reda
% 3 u modu tmod, sa preostalim indeksima fiksiranim na j i
% k.

tdim=size(A);
ind=1:3;
ip=ind(ind=tmod);
Ap=permute(A,[tmod,ip]);
Av=reshape(Ap(:,j,k),tdim(tmod),1);

end

MATLAB kod

function Ao=odsj_tenz_mod(A,tmod,i)
% Ao=odsj_tenz_mod(A,tmod,j,k) vraca odsjecak tenzora A
% reda 3 u modu tmod, za i_tmod=i.

tdim=size(A);
ind=1:3;
ip=ind(ind=tmod);
Ap=permute(A,[ip,tmod]);
Ao=reshape(Ap(:,:,i),tdim(ip));

end

često je korisno prikazati tenzor u obliku matrice. Stoga definiramo matricu tenzora po modu n kao matricu A_{(n)} koja se dobije tako da vektore iz moda n složimo kao stupce u matricu A_{(n)}. Poredak kojim se vektori iz moda n preslikavaju u stupce nije bitan, dok god se isti poredak koristi u svim izračunima.

Matricizacija tenzora (eng. unfold) u modu n od \mathcal{A} označava se s

A_{(n)} \in {\mathbb{R}}^{I_{n} \times (I_{1} \times \dots \times I_{n-1} \times I_{n+1} \times \dots \times I_{N})}.

Tenzorski produkt u modu n tenzora \mathcal{A} \in \mathbb{R}^{I_{1} \times I_{2} \times \dots \times I_{N}} s matricom U \in \mathbb{R}^{J_{n} \times I_{n}}, označen s \mathcal{A} \times_{n}U, je

(I_{1} \times \dots \times I_{n-1} \times J_{n} \times I_{n+1} \times \dots \times I_{N})

tenzor čiji elementi su zadani s

(\mathcal{A} \times_{n} U)_{i_{1}i_{2} \dots i_{n-1}j_{n}i_{n+1} \dots i_{N} } \stackrel{def}{=}\sum_{i_{n}}^{}a_{i_{1}i_{2} \dots i_{n-1}i_{n}i_{n+1} \dots i_{N}}u_{j_{n}i_{n}}.

Zbog jednostavnosti ograničavamo se na tenzore reda 3, \mathcal{A} = (a_{ijk}) \in \mathbb{R}^{I_{1} \times I_{2} \times I_{3}}. Takav tenzor možemo vizualizirati na sljedeći način:

Uvedimo sada osnovne pojmove za tenzor reda 3, \mathcal{A} \in \mathbb{R}^{I_{1} \times I_{2} \times I_{3}}. Dimenzije tenzora \mathcal{A} \in \mathbb{R}^{I_{1} \times I_{2} \times I_{3} } su: I_{1}, I_{2} i I_{3}.

2.1Osnovni koncepti tenzora

Prvo definiramo skalarni produkt dvaju tenzora istog reda i jednakih dimenzija:

Definicija 3. Skalarni produkt dvaju tenzora istih dimenzija \mathcal{A},\mathcal{B} \in \mathbb{R}^{I_{1} \times I_{2} \times I_{3}} je suma umnožaka njihovih elemenata, tj.

(2)

\langle \mathcal{A},\mathcal{B} \rangle=\sum_{i,j,k} a_{ijk} b_{ijk}.

Pripadna norma je

Definicija 4. Norma tenzora \mathcal{A} \in \mathbb{R}^{I_{1} \times I_{2} \times I_{3}} je kvadratni korijen sume svih kvadrata njegovih elemenata, tj.

\Vert \mathcal{A}\Vert = \langle{\mathcal{A},\mathcal{A}}\rangle^{1/2}=\Bigg(\sum_{i,j,k} a_{ijk}^{2}\Bigg)^{1/2}.

Ako gledamo gornje definicije na matricama (dvodimenzionalnim tenzorima) vidimo da je to Frobeniusova norma.

Sljedeće što definiramo je množenje u modu 1 matrice s tenzorom.

Definicija 5. Množenje u modu 1 tenzora \mathcal{A} \in \mathbb{R}^{I_{1} \times I_{2} \times I_{3}} matricom \mathcal{U}\in\mathbb{R}^{l_{0}\times I_{1}} u oznaci \mathcal{A}\times_{1} U, je l_{0}\times I_{2} \times I_{3} tenzor dan s

(\mathcal{A}\times_{1} U)(j,i_{2},i_{3})=\sum_{k=1}^{I_{1}} u_{j,k}a_{k,i_{2},i_{3}}.

Uspredbe radi, uočimo da za množenje matrica vrijedi

A \times_{1} U = UA, \hspace{5mm} (UA)(i,j)=\sum_{k=1}^{l}u_{i,k}a_{k,j}.

Znamo da je množenje matrica ekvivalentno množenju svakog stupca iz \mathcal{A} matricom U. Isto vrijedi i za množenje tenzora matricom u modu 1. Svi stupčani vektori iz tenzora \mathcal{A} se množe matricom U.

Slično množenje u modu 2 tenzora s matricom V

(\mathcal{A}\times_{2} V)(i_{1},j,i_{3})=\sum_{k=1}^{I_{2}}v_{j,k}a_{i_{1},k,i_{3}}

znači da su svi retci tenzora pomnoženi s matricom V. Opet uočavamo da je množenje u modu 2 matrice s V ekvivalentno matričnom množenju s V^{T} zdesna,

A\times_{2} V = AV^{T};

Množenje u modu 3 se dobije analogno.

Ponekad je zgodno matricizirati tenzor u matricu.

Matricizacija tenzora \mathcal{A} je definirana kroz tri moda (koristeći MATLAB-ovu notaciju):

\begin{align*} \text{unfold}_{1}(\mathcal{A}):=&A_{(1)}:=(\mathcal{A}(:,1,:)\hspace{5mm} \mathcal{A}(:,2,:) \hspace{5mm}\dots \hspace{5mm}\mathcal{A}(:,I_{2},:)) \hspace{1cm} \in \mathbb{R} ^{I_{1}\times I_{2} I_{3} }, \\ \text{unfold}_{2}(\mathcal{A}):=&A_{(2)}:=(\mathcal{A}(:,:,1)^{T}\hspace{5mm} \mathcal{A}(:,:,2)^{T} \hspace{5mm}\dots \hspace{5mm}\mathcal{A}(:,:,I_{3})^{T}) \hspace{4mm} \in \mathbb{R} ^{I_{2}\times I_{1} I_{3} }, \\ \text{unfold}_{3}(\mathcal{A}):=&A_{(3)}:=(\mathcal{A}(1,:,:)^{T}\hspace{5mm} \mathcal{A}(2,:,:)^{T} \hspace{5mm}\dots \hspace{5mm}\mathcal{A}(I_{1},:,:)^{T}) \hspace{5mm} \in \mathbb{R} ^{I_{3}\times I_{1} I_{2} }. \end{align*}

Vrijedi i sljedeće:

(1)	{Stupčani vektori od \mathcal{A} su stupčani vektori od A_{(1)}}.
(2)	{Retci od \mathcal{A} su stupčani vektori od A_{(2)}}.
(3)	{Prostorni vektori od \mathcal{A} su stupčani vektori od A_{(3)}}.

\text{Unfold}_{1} od \mathcal{A} je ekvivalentan dijeljenju tenzora na odsječke \mathcal{A}(:,i,:) (koji su matrice) i slaže ih u dugu matricu A_{(1)}.

MATLAB kod

function Au=tenz_unfold(A,tmod)
% Au=tenz_unfold(A,tmod) vraca matricizaciju tenzora A reda
% 3 po modu tmod.

tdim=size(A);
Au=[];
io=mod(tmod,3)+1;
for i=1:tdim(io)
    if (tmod==1)
        Au=[Au,odsj_tenz_mod(A,2,i)];
    else
        Au=[Au,odsj_tenz_mod(A,io,i)'];
    end
end

end

Slika 7: Matricizacija (I_{1} \times I_{2} \times I_{3}) tenzora \mathcal{A} na (I_{1} \times I_{2} I_{3}) matricu A_{(1)}, (I_{2} \times I_{3} I_{1}) matricu A_{(2)} i (I_{3} \times I_{1} I_{2}) matricu A_{(3)}(I_{1} = I_{2} = I_{3} = 4).

Kao što nam je korisno prikazati tenzor u obliku matrice tako nam je ponekad korisno tenzorificirati matricu odnosno matricu pretvoriti u tenzor. Tenzorifikacija je inverz matricizacije odnosno operator fold je inverz operatora unfold pa vrijedi

\text{fold}_{i}(\text{unfold}_{i}(\mathcal{A}))=\mathcal{A}.

MATLAB kod

function A=tenz_fold(Au,tmod,tdim)
% A=tenz_fold(Au,tmod,tdim) tenzorificira matricu Au koja
% je matricizirana pomocu Au=tenz_unfold(A,tmod), natrag u
% polazni tenzor dimenzija tdim(1) x tdim(2) x tdim(3).

A=[];
[dim1,dim2]=size(Au);
if (dim1=tdim(tmod) && dim2=prod(tdim(tdim=tmod)))
    fprintf(1,'Krive dimenzije!\n');
    return;
end

io=mod(tmod,3)+1; ib=mod(tmod-2,3)+1; bdim=tdim; bdim(io)=1;
for i=1:tdim(io)
    switch(tmod)
        case 1
            A(:,i,:)=reshape(Au(:,(i-1)*tdim(ib)+1:
                                i*tdim(ib)),bdim);
        case 2
            A(:,:,i)=reshape(Au(:,(i-1)*tdim(ib)+1:
                                i*tdim(ib))',bdim);
        case 3
            A(i,:,:)=reshape(Au(:,(i-1)*tdim(ib)+1:
                                i*tdim(ib))',bdim);
    end
end

end

Korištenjem unfold-fold operacija, možemo formulirati matrično množenje ekvivalentno u modu i tenzorskom množenju:

(3)

\mathcal{A}\times_{i}U=\text{fold}_{i}(U\ \text{unfold}_{i}(\mathcal{A}))=\text{fold}_{i}(UA_{(i)}).

MATLAB kod

function B = tenz_mult(A, U, tmod)
% B = tenz_mult(A, U, mod) vraca tenzorski produkt u modu
% tmod tenzora A reda 3 sa matricom U.

B=[];
Au=tenz_unfold(A,tmod);
udim=size(U);
audim=size(Au);

if (udim(2)=audim(1))
    fprintf(1,'Krive dimenzije!\n');
    return;
end

tdim = size(A);
switch(tmod)
    case 1
        B=tenz_fold(U*Au,tmod,[udim(1),tdim(2:3)]);
    case 2
        B=tenz_fold(U*Au,tmod,[tdim(1),udim(1),tdim(3)]);
    case 3
        B=tenz_fold(U*Au,tmod,[tdim(1:2),udim(1)]);
end

end

2.2Tenzorski SVD (HOSVD)

Matrični SVD može se generalizirati na više načina kako bi dobili tenzorski. Mi promatramo jedan koji se često naziva "Higher order SVD" (HOSVD).

Vidjeli smo da matrice možemo promatrati kao tenzore reda 2. Koristeći tenzorsku notaciju, jednadžbu (1) iz Teorema 1 (SVD) sada možemo zapisati kao

A = U\Sigma V^{T} = \Sigma \times_{1} U \times_{2} V = S \times_{1} U^{(1)} \times_{2} U^{(2)}

isto vrijedi i za tenzore višeg reda. O tome nam više govori sljedeći teorem.

Teorem 6. (HOSVD) Tenzor \mathcal{A} \in \mathbb{R} ^{l \times m \times n} može se zapisati kao

(4)

\mathcal{A} = \mathcal{S} \times_{1} U^{(1)} \times_{2} U^{(2)} \times_{3} U^{(3)},

gdje su U^{(1)} \in \mathbb{R}^{l \times l},U^{(2)} \in \mathbb{R}^{m \times m} i U^{(3)} \in \mathbb{R}^{n \times n} ortogonalne matrice. \mathcal{S} je tenzor istih dimenzija kao \mathcal{A}. Svaka dva odsječka tenzora \mathcal{S} su ortogonalna u smislu skalarnog produkta:

\langle \mathcal{S}(i,:,:),\mathcal{S}(j,:,:) \rangle = \langle\mathcal{S}(:,i,:),\mathcal{S}(:,j,:)\rangle = \langle\mathcal{S}(:,:,i),\mathcal{S}(:,:,j)\rangle = 0

za i \neq j. Singularne vrijednosti u modu 1 su definirane s

\sigma_{j}^{(1)} = ||\mathcal{S}(j,:,:)||_{F} , \hspace{1cm} j=1,\dots,l

i one su sortirane silazno

(5)

\sigma_{1}^{(1)} \geq \sigma_{2}^{(1)} \geq \dots \geq \sigma_{l}^{(1)} .

Singularne vrijednosti u ostalim modovima i njihovo sortiranje je analogno.

Ortogonalni tenzor \mathcal{S} nazivamo jezgreni tenzor tenzora \mathcal{A}. HOSVD je vizualiziran na Slici 8.

Slika 8: Vizualizacija HOSVD-a.

Koristeći tenzorsku dekompoziciju, svaki tenzor reda N možemo prikazati kao produkt

(6)

\mathcal{A}=\mathcal{S} \times_{1} U^{(1)} \times_{2} U^{(2)} \times_{3} \dots \times_{N} U^{(N)}

gdje nam je \mathcal{S} jezgreni tenzor, a U_{n},\ n=1,2, \dots ,N ortogonalne matrice.

Iz dokaza prethodnog teorema može se zapravo vidjeti kako se računa HOSVD određenog tenzora \mathcal{A}:

(1)	Matrica U^{(i)} u modu i može se direktno naći kao lijeva singularna matrica od matricizacije tenzora \mathcal{A} u modu i: A_{(i)} = U^{(i)}\Sigma^{(i)} V^{(i)^{T}}.
(2)	Nakon toga, jezgreni tenzor \mathcal{S} može se izračunati prebacivanjem matrica singularnih vekotora na lijevu stranu u jednadžbi (6): \mathcal{S} = \mathcal{A}\times_{1} U^{(1)^{T}} \times_{2} U^{(2)^{T}} \times_{3} \dots \times_{N} U^{(N)^{T}}.

Zbog toga se računanje HOSVD-a tenzora reda N svodi na računanje N različitih matričnih SVD-a matrica formata (I_{n} \times I_{1} I_{2} \cdots I_{n-1} I_{n+1} \cdots I_{N}).

Ponekad se događa da je dimenzija od jednog moda veća od produkta dimenzija drugih modova. Pretpostavimo, npr. da je \mathcal{A} \in \mathbb{R}^{l \times m \times n} gdje je l \gt mn. Može se pokazati da tada za tenzor \mathcal{S} vrijedi

(7)

\mathcal{S}(i,:,:) = 0, \hspace{1cm} i \gt mn,

i možemo odbiti dio s nulama tenzora \mathcal{S} te (4) napisati kao tanki HOSVD

(8)

\mathcal{A} = \widehat{\mathcal{S}} \times_{1} \widehat{U}^{(1)} \times_{2} U^{(2)} \times_{3} U^{(3)},

gdje je \widehat{\mathcal{S}} \in \mathbb{R}^{mn \times m \times n } i \widehat{U}^{(1)} \in \mathbb{R}^{l \times mn}.

MATLAB kod

function [S,U1,U2,U3]=tenz_hosvd(A)
% [S,U1,U2,U3]=tenz_hosvd(A) racuna HOSVD tenzora A reda 3.

[U1,S1,V1]=svd(tenz_unfold(A,1));
[U2,S2,V2]=svd(tenz_unfold(A,2));
[U3,S3,V3]=svd(tenz_unfold(A,3));
S=tenz_mult(tenz_mult(tenz_mult(A,U1',1),U2',2),U3',3);
sdim=size(S);

%Slucaj tankog HOSVD-a
psd12=sdim(1)*sdim(2);
psd13=sdim(1)*sdim(3);
psd23=sdim(2)*sdim(3);

if (sdim(1)>psd23)
S=S(1:psd23,1:sdim(2),1:sdim(3));
U1=U1(1:sdim(1),1:psd23);
return;
end

if (sdim(2)>psd13)
S=S(1:sdim(1),1:psd13,1:sdim(3));
U2=U2(1:sdim(2),1:psd13);
return;
end

if (sdim(3)>psd12)
S=S(1:sdim(1),1:sdim(2),1:psd12);
U3=U3(1:sdim(3),1:psd12);
return;
end

2.3Aproksimacija tenzora HOSVD-om

I HOSVD se može koristiti za kompresiju tenzora. Budući da je masa jezgrenog tenzora \mathcal{S} koncentirana za male vrijednosti od sva tri indeksa, moguće je "stisnuti" podatke u sva tri moda HOSVD-om. Pretpostavimo sada da smo podatke stisnuli u manji tenzor gdje ćemo imati k_{i} stupaca u modu i. Neka je U_{k_{i}}^{(i)} = U^{(i)}(:,1:k_{i}) i \hat{\mathcal{S}} = \mathcal{S}(1:k_{1},1:k_{2},1:k_{3}). Zatim razmotrimo aproksimaciju

\mathcal{A}\approx \widehat{\mathcal{A}}=\widehat{\mathcal{S}}\times_{1} U_{k_{1}}^{(1)} \times_{2} U_{k_{2}}^{(2)} \times_{3} U_{k_{3}}^{(3)}.

Ilustrirajmo to na sljedećoj slici:

Na ovaj način smo uz minimalne gubitke uštedjeli memoriju. Tenzor \mathcal{A}\in \mathbb{R}^{l\times m \times n} ima ukupno l \cdot m \cdot n elemenata, dok za njegovu aproksimaciju \widehat{\mathcal{A}} moramo pamtiti ukupno k_{1} \cdot k_{2} \cdot k_{3} + l\cdot k_{1} + m\cdot k_{2} + n \cdot k_{3} elemenata.

Ako je tenzor \mathcal{A}\in \mathbb{R}^{1000\times 1000 \times 1000} onda on ima 1000 \cdot 1000 \cdot 1000 = 10^{9} elemenata, dok njegova aproksimacija \widehat{\mathcal{A}} za k_{1}=k_{2}=k_{3}=100 ima 10^{6} elemenata u \widehat{\mathcal{S}}, 1000 \cdot 100 = 10^{5} elemenata u U_{k_{1}}^{(1)},U_{k_{2}}^{(2)} i U_{k_{3}}^{(3)}, ukupno 1.3\cdot 10^{6} elemenata. što znaći da umjesto da koristimo 1 000 000 000 elemenata mi korisitmo samo 1 300 000 elemenata, a to je ušteda od 997 000 000 elemenata, odnosno umjesto da zauzmemo 3GB memorije zauzimamo samo 3.9MB.

3Prepoznavanje lica korištenjem HOSVD-a

Ljudska bića su vrlo vješta pri prepoznavanju lica čak i kada izraz lica, osvjetljenje, kut gledanja itd. variraju. Razviti automatske postupke za prepoznavanje lica koji su robusni s obzirom na različite uvjete, izazovan je istraživački problem koji je istražen pomoću nekoliko različitih pristupa. Analiza glavnih komponenti (eng. principal component analysis, PCA), temeljena na SVD-u, popularna je tehnika koja često ide pod imenom "eigenfaces". Međutim, ova metoda je najbolja kada su sve fotografije nastale pod sličnim uvjetima, i ne radi dobro kad se mijenjaju neki faktori okoline.

Nedavno su istraživane metode za multilinearnu analizu skupa fotografija. Konkretno, problem prepoznavanja lica razmatran je korištenjem tenzorskog modela, TensorFaces pristupa. I to tako da modovi tenzora predstavljaju drukčiji način gledanja, npr. osvjetljenje ili izraz lica, postalo je moguće poboljšati preciznost algoritma prepoznavanja u usporedbi s PCA metodom.

U ovom ćemo odsječku opisati metodu tenzorskog prepoznavanja lica, koja se odnosi na TensorFaces. Budući da se radi o fotografijama, koje se često pohranjuju kao matrice m \times n, s m i n reda 100-500, izračuni za svako lice koje treba identificirati su prilično teški. Razmotrit ćemo kako se tenzorski SVD (HOSVD) također može koristiti za smanjenje dimenzije u svrhu smanjenja broja operacija.

3.1Tenzorski prikaz fotografija

Pretpostavimo da imamo kolekciju fotografija od n_{p} osoba, gdje je svaka fotografija m_{i_{1}} \times m_{i_{2}} matrica s m_{i_{1}} m_{i_{2}} = n_{i} elemenata. Pretpostavljamo da su stupci fotografija složeni tako da svaka fotografija predstavlja vektor u \mathbb{R}^{n_{i}}. Nadalje pretpostavljamo da je svaka osoba fotografirana u n_{e} različitih izraza lica. često je n_{i} \geq 5000, i obično je n_{i} znatno veći od n_{e} i n_{p}. Takva kolekcija fotografija je spremljena u tenzor:

(9)

\mathcal{A} \in \mathbb{R}^{n_{i} \times n_{e} \times n_{p}}

Pozivamo se na različite modove kao što su mod fotografije (eng. the image mode), mod izraza lica (eng. the expression mod) i mod osobe (eng. the person mode), zbog toga korisitmo indekse i,e,p u (9).

Ako, primjerice, također imamo fotografije svake osobe s različitim osvjetljenjem, kutem gledanja, itd., onda bi mogli predstavljati kolekciju fotografija tenzorom višeg reda. Radi jednostavnosti ovdje promatramo samo tenzore reda 3. Generalizacija tenzorima višeg reda je jasna.

Primjer 7. Prethodno smo obradili fotografije od 10 osoba iz baze podataka Yale Face koje smo postavili na 112 \times 78 piksela i pohranili u vektor duljine 8736. Pet fotografija je prikazano na sljedećoj slici.

Slika 9: Osoba 1 s pet različitih izraza lica (iz Yale Face Database).

Svaka osoba je fotografirana u ukupno 11 različitih izraza lica.

Redosljed modova je naravno proizvoljan; u svrhu ilustriranja pretpostavljat ćemo redosljed iz (9). Međutim kako bi naglasili proizvoljnost, koristit ćemo oznaku \times _{e} za množenje tenzora matricom u modu izraza lica (the expression mode), i slično za druge modove. Sada pretpostavljamo da je n_{i} \gg n_{e} n_{p} i pišemo tanki HOSVD (Pogledati Teorem 6 i (8)),

\mathcal{A}= \mathcal{S} \times_{i} F \times_{e} G \times_{p} H,

gdje je \mathcal{S} \in \mathbb{R}^{n_{e}n_{p} \times n_{e} \times n_{p}} jezgra tenzora \mathcal{A}, F\in \mathbb{R}^{n_{i} \times n_{e}n_{p}} ima ortogonalne stupce, i G \in \mathbb{R}^{n_{e} \times n_{e}} i H \in \mathbb{R}^{n_{p} \times n_{p}} su ortogonalne matrice.

3.2Prepoznavanje lica

Sada ćemo razmatrati problem klasifikacije kako slijedi:

Za danu fotografiju nepoznate osobe, koju predstavlja vektor u \mathbb{R}^{n_{i}} odredit ćemo koju od n_{p} osoba predstavlja ili odlučiti da nepoznata osoba nije u bazi podataka.

Za klasifikaciju pišemo HOSVD (4) u sljedećem obliku:

(10)

\mathcal{A} = \mathcal{C}\times_{p} H, \hspace{1cm} \mathcal{C} = \mathcal{S}\times_{i} F \times_{e} G.

Za određeni izraz lica e imamo

(11)

\mathcal{A}(:,e,:)=\mathcal{C}(:,e,:)\times_{p} H.

Očito tenzore \mathcal{A}(:,e,:) i \mathcal{C}(:,e,:) možemo promatrati kao matrice, koje označavamo s A_{e} i C_{e}. Stoga, za sve izraze imamo linearne relacije

(12)

A_{e} = C_{e} H^{T}, \hspace{1cm} e=1,2,\cdots , n_{e}

Imajmo na umu da se ista (ortogonalna) matrica H pojavljuje u svih n_{e} relacija. S H^{T} = (h_{1} \cdots h_{n_{p}}), stupac p iz (12) može biti zapisan kao

(13)

a_{p}^{(e)} = C_{e} h_{p}

Možemo interpretirati (12) i (13) na sljedeći način:

Stupac p od matrice A_{e} sadrži sliku osobe p u izrazu e. Stupci matrice C_{e} su bazni vektori za izraz e, i red p matrice H, tj, h_{p}, sadrži koordinate fotografija osobe p u toj bazi. Nadalje isti h_{p} sadrži koordinate fotografija osobe p u svim izraznim bazama.

Zatim pretpostavimo da je z \in \mathbb{R}^{n_{i}} slika nepoznate osobe u nepoznatom izrazu (iz n_{e}) i da ju želimo klasificirati. Taj z ćemo zvati testna slika. Očito, ako je slika osobe p u izrazu e, onda su koordinate vektora z u toj bazi jednake koordinatama vektora h_{p}. Dakle, možemo klasificirati z računanjem njegovih koordinata u svim bazama ekspresije i provjeravajući, za svaki izraz, podudaraju li se koordinate od z (ili se gotovo podudaraju) s elementima bilo kojeg reda matrice H.

Koordinate od z u izraznoj bazi e mogu se naći rješavanjem problema najmanjeg kvadrata

(14)

\min_{\alpha_{e}} \Vert C_{e} \alpha_{e} - z\Vert _{2}

Klasifikacijski algoritam

for e = 1,2, \cdots, n_{e}

Riješi \text{min}_{\alpha_{e}} \Vert C_{e} \alpha_{e} - z\Vert _{2}

for p=1,2,\cdots, n_{p}

if \Vert \alpha_{e} - h_{p}\Vert _{2} \lt tol, onda klasificiraj kao osobu p i stani.

end

Količina posla u ovom algoritmu je velika: za svaku test sliku z moramo riješiti n_{e} problema najmanjih kvadrata (14) s C_{e} \in \mathbb{R}^{n_{i} \times n_{p}}.

4Primjeri dobiveni MATLAB rutinama

Program smo testirali na 10 osoba fotografiranih u 10 različitih ekspresija(izraza) lica. Fotografije su spremljene u matricu tako da svaki stupac predstavlja jednu fotografiju i to na način da prvih 10 stupaca predstavlja prvu osobu u svih 10 ekspresija, drugih 10 stupaca predstavlja drugu osobu itd. Svaka fotografija je dimenzije 64 \times 64 što znači da je matrica dimenzije 4096\times 100. Pogledajmo sada fotografije tih osoba u prvom izrazu lica:

Slika 10: 10 osoba u prvom izrazu lica.

Svaka od tih osoba je fotografirana u 10 različitih izraza lica, pa pogledajmo na prvoj osobi koji su to sve izrazi: \nopagebreak[4]

4.1Klasifikacija

Za potrebe prepoznavanja lica uzeli smo prvih 5 osoba u prve 3 ekspresije lica (15 fotografija) i stavili ih u bazu, te na njima "trenirali" program. Nakon toga smo izbacili te fotografije i na preostalim fotografijama testirali program. Preostalo je po 7 fotografija za svaku osobu koja je u bazi, a po 10 od osoba koje nisu u bazi (ukupno 35 fotografija osoba koje su u bazi i 50 fotografija osoba koje nisu u bazi). Naš cilj je da danu testnu fotografiju program klasificira kao jednu od tih 5 osoba ili da vrati: "Tražena osoba nije u bazi!". Odnosno, ukoliko je testna fotografija jedna od tih 7 fotografija da program prepozna tu osobu kao odgovarajuću osobu iz baze, a ako je jedna od 10 fotografija osoba koje nisu u bazi da vrati: "Tražena osoba nije u bazi!". Tolerancija u ovom radu iznosi 0.475, a do nje dolazimo eksperimentima.

Uzmimo sada za testnu fotografiju proizvoljnu fotografiju iz skupa od 35 fotografija osoba koje su u bazi i na njoj testirajmo program. Pogledajmo rezultate na sljedećim slikama: (Lijeva fotografija predstavlja osobu koju želimo klasificirati, a desna klasificiranu osobu.)

Vidimo da je program dobro prepoznao lica. Za sljedeće fotografije je program vratio: "Tražena osoba nije u bazi!".

što također vidimo da je dobro jer niti jedna od tih osoba nije u prvih 5 osoba na kojima smo trenirali naš program.

Napomenimo na kraju da program nije savršen i da se može dogoditi da krivo klasificira osobu. Primjer krive klasifikacije: Uzeli smo novu 11. osobu i pokušali je klasificirati.

Klasifikacija očito nije dobra jer to nisu iste osobe!

Da bismo to spriječili možemo smanjiti toleranciju, ali u tom slučaju se može dogoditi da osoba koja je u bazi ne bude prepoznata, odnosno da program vrati: "Tražena osoba nije u bazi!".

Pogledajmo i takav primjer: (Tolerancija u ovom primjeru iznosi 0.35).

Za gornju fotografiju je program vratio: "Tražena osoba nije u bazi!", a trebao ju je klasificirati kao:

Unatoč tome smatramo da je "manja" pogreška ako program ne prepozna osobu koju bi trebao, nego da osoba koja nije u bazi bude prepoznata kao neka osoba koja je u bazi. Iz tih razloga ipak uzimamo manju toleranciju do koje dolazimo eksperimentima.

Bibliografija

[1]	L. Elden, Matrix methods in data mining and pattern recognition, Philadelphia, SIAM., 2007.
[2]	L. De Lathauwer, B. De Moor, and J. Vandewalle. A multilinear singular value decomposition. SIAM J. Matrix Anal. Appl., 21:1253-1278, 2000.
[3]	J. Demmel. Applied Numerical Linear Algebra. SIAM . MIT , 1996.
[4]	T. G. Kolda, Multilinear Operators for Higher Order Decompositions, Tech. Report SAND2006-2081, 2006.
[5]	Mladen Rogina, Sanja Singer, Saša Singer. Numerička analiza. PMF - Matematički odsjek, Zagreb, 2003.
[6]	Z. Drmač. Bilješke s predavanja iz kolegija Uvod u složeno pretraživanje podataka, PMF - Matematički odsjek, Zagreb, 2016.
[7]	A. Novak, D. Pavlović. Dekompozicija matrice na singularne vrijednosti i primjene. math.e, Zagreb, 2013.

Floyd-Warshallov algoritam u tropskoj geometriji

Zlatko Erjavec, Drago Kovačec

zlatko.erjavec@foi.hr, drago.kovacec@foi.hr

Sažetak

U članku se pojašnjavaju osnovni pojmovi tropske geometrije te njena primjena u rješavanju problema određivanja najkraćeg puta u težinskom grafu Floyd-Warshallovim algoritmom.

1Uvod

Tropska geometrija je relativno novo područje u matematici, a naziv "tropska geometrija" osmislili su francuski matematičari u čast brazilskom matematičaru Imre Simonu, pioniru u tom području. Stoga pridjev "tropska" nema neko posebno značenje osim asocijacije na Brazil kao tropsko područje.

Jednostavnost aritmetike tropske geometrije omogućila joj je brojne primjene od ekonomije preko biologije do računarstva. Više o primjenama može se naći u [2].

U ovom članku pokazat ćemo na koji se način aritmetika tropske geometrije može primijeniti u rješavanju problema pronalaska najkraćeg puta. Bilo da govorimo o putu kamiona od skladišta do odredišta ili o najkraćem putu među serverima u računalnoj mreži, problem se svodi na nalaženje najkraćeg puta u težinskom grafu. Navedeni problem rješava Floyd-Warshallov algoritam.

2Tropska geometrija

Osnovna struktura tropske geometrije je tropski poluprsten, uređena trojka \left(\mathbb{R }\cup \, \lbrace \infty \rbrace , \ \oplus ,\ \odot \right) sastavljena od skupa realnih brojeva proširenog beskonačnošću te dvije međusobno usklađene operacije, tropskog zbrajanja i tropskog množenja (vidi [3]).

2.1Tropsko zbrajanje

Suma dvaju brojeva u tropskoj aritmetici definira se kao minimum tih dvaju brojeva

(1)

x \oplus y := \min (x, y).

Primjer 1. Tropsko zbrajanje

3 \oplus 5= 3 \qquad \text{i} \qquad 7 \oplus 2 = 2.

2.2Tropsko množenje

Produkt dvaju brojeva u tropskoj aritmetici definira se kao uobičajen zbroj tih dvaju brojeva

(2)

x \odot y := x + y.

Primjer 2. Tropsko množenje

3 \odot 5 = 8 \qquad \text{ i} \qquad 7 \odot 2 = 9.

Obje definirane računske operacije imaju neutralne elemente. Za tropsko zbrajanje neutralni element je beskonačno, dok je za tropsko množenje neutralni element nula

a \oplus \infty = a\qquad \text{ i} \qquad a \odot 0 = a.

Također vrijedi,

a \oplus 0 = \begin{cases} 0 ,& \text{za}\ a\geq 0\\ a ,& \text{za}\ a\lt 0 \\ \end{cases} \qquad \text{ i} \qquad a \odot \infty = \infty.

Nadalje, obje operacije su komutativne i asocijativne te vrijedi distributivnost množenja u odnosu na zbrajanje.

\bullet	Komutativnost a \oplus b = b \oplus a \qquad \text{ i} \qquad a \odot b = b \odot a.
\bullet	Asocijativnost (a \oplus b) \oplus c = a \oplus (b \oplus c) \quad \text{ i} \quad (a \odot b) \odot c = a \odot (b \odot c).
\bullet	Distributivnost a \odot (b \oplus c) = a \odot b \oplus a \odot c.

Primjer 3. Distributivnost tropskog množenja prema zbrajanju

\begin{eqnarray*} 4 \odot (2 \oplus 3) &=& 4 \odot 2 \oplus 4 \odot 3\\ 4 \odot 2 &=& 6 \oplus 7 \\ 6 &=& 6. \end{eqnarray*}

2.3Tropski polinom

Neka su x_{1}, x_{2}, \ldots x_{n} varijable koje predstavljaju elemente tropskog poluprstena. Monom se definira kao bilo koji produkt tih varijabli, pri čemu je mogućnost njihova ponavljanja dozvoljena.

Koristeći komutativnost i asocijativnost, možemo presložiti produkt i zapisati ga u uobičajenom obliku koristeći potencije, imajući na umu da x^{2} znači x \odot x, a ne x \cdot x. Npr.

x_{2} \odot x_{1} \odot x_{3} \odot x_{1} \odot x_{2} \odot x_{2} = x_{1}^{2}\,x_{2}^{3}\,x_{3}.

Svakom monomu možemo pridružiti funkciju sa \mathbb{R}^{n} u \mathbb{R}. Kada bismo takvu funkciju evaluirali u klasičnoj aritmetici, dobili bismo linearnu funkciju:

\begin{eqnarray*} f(x_{1}, x_{2}, x_{3})&=& x_{2} \odot x_{1} \odot x_{3} \odot x_{1} \odot x_{2} \odot x_{2} \\ &=& x_{2} + x_{1} + x_{3} + x_{1} + x_{2} +x_{2} \\ &=& 2 x_{1}+ 3x_{2} +x_{3}. \end{eqnarray*}

Iako smo u primjeru koristili pozitivne eksponente, monomi su definirani i za cjelobrojne eksponente. Stoga, možemo zaključiti da su tropski monomi linearne funkcije s cjelobrojnim koeficijentima.

Tropski polinom je konačna linearna kombinacija tropskih monoma: p(x_{1}, x_{2}, \ldots x_{n})=a \odot x_{1}^{i_{1}} x_{2}^{i_{2}} \cdots x_{n}^{i_{n}} \oplus b \odot x_{1}^{j_{1}} x_{2}^{j_{2}} \cdots x_{n}^{j_{n}} \oplus \cdots

Primjer 4. Tropski polinom u jednoj varijabli

p(x)=(2 \odot x^{3} ) \oplus (1\odot x^{2} ) \oplus (3 \odot x) \oplus 2= \min \lbrace 2+3x, 1+2x, 3+x, 2\rbrace.

Primijetite da u tropskoj geometriji polinomi

\begin{eqnarray*} p_{1}(x)&=&x^{2} \oplus (1 \odot x) \oplus 2= \min \lbrace 2x, 1+x, 2\rbrace = \min \lbrace 2x, 2\rbrace \quad \text{i} \\ p_{2}(x)&=&x^{2} \oplus (17 \odot x) \oplus 2= \min \lbrace 2x, 17+x, 2\rbrace = \min \lbrace 2x, 2\rbrace \end{eqnarray*}

imaju istu vrijednost. Dakle, prikaz neke funkcije u obliku tropskog polinoma nije jednoznačan.
Uslijed specifičnosti definicije množenja i nule kao neutralnog elementa, svi binomni koeficijenti tropskog polinoma jednaki su nuli (u Pascalovom trokutu su samo nule!). Posljedica navedenog je činjenica da u tropskoj geometriji za sve potencije binoma vrijedi tzv. "brucoški san".

Primjer 5. "Brucoški san" za kvadrat binoma

\begin{eqnarray*}(x \oplus y)^{2} &=& (x \oplus y) \odot (x \oplus y)\\ &=& 0 \odot x^{2} \oplus 0 \odot xy \oplus 0 \odot y^{2} \\ &=& (0 + x^{2}) \oplus (0 + xy) \oplus (0 + y^{2}) \\ &=& x^{2} \oplus xy \oplus y^{2} \\ &=& \min \lbrace x^{^{2}}, xy, y^{2} \rbrace \\ &=& \min \lbrace x^{^{2}}, y^{2} \rbrace \\ &=& x^{2} \oplus y^{2}. \end{eqnarray*}

2.4Tropski skalarni produkt

Tropski skalarni produkt definira se analogno klasičnom matričnom produktu jednoretčane i jednostupčane matrice

\begin{eqnarray*} (u_{1}, u_{2}, u_{3}) \odot (v_{1}, v_{2}, v_{3})^{T} &=& u_{1} \odot v_{1} \oplus u_{2} \odot v_{2} \oplus u_{3} \odot v_{3} \\ &=& \min \left\lbrace u_{1} + v_{1}, u_{2} + v_{2}, u_{3} + v_{3} \right\rbrace. \end{eqnarray*}

Primjer 6. Tropski skalarni produkt

\begin{eqnarray*}(2, 4, -3) \odot (3, 5, -5) &=& (2 \odot 3) \oplus (4 \odot 5) \oplus ((-3) \odot (-5))\\ & =& \min \lbrace 5, 9, -8\rbrace =-8.\end{eqnarray*}

2.5Tropsko zbrajanje matrica

Tropsko zbrajanje matrica definira se analogno klasičnom zbrajanju matrica, po elementima, korištenjem tropskog zbrajanja.

Primjer 7. Tropsko zbrajanje matrica

\begin{pmatrix} 0 & 2 \\ 3 & 1 \end{pmatrix} \oplus \begin{pmatrix} 3 & 1 \\ 1 & 1 \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ 1 & 1 \end{pmatrix}.

2.6Tropsko množenje matrica

Tropsko množenje matrica definira se analogno klasičnom množenju matrica. Element produkta dviju matrica dobije se kao tropski skalarni produkt odgovarajućeg retka prve i odgovarajućeg stupca druge matrice.

Primjer 8. Tropsko množenje matrica

\begin{pmatrix} 0 & 2 \\ 3 & 1 \end{pmatrix} \odot \begin{pmatrix} 3 & 1 \\ 1 & 1 \end{pmatrix} = \begin{pmatrix} 3 & 1 \\ 2 & 2 \end{pmatrix}.

3Grafovi i problem najkraćeg puta

Graf G se definira kao uređen par skupova G=(V, E) pri čemu je skup V skup vrhova, a skup E je skup bridova. Skupovi V i E su disjunktni, a svaki brid e \in E spaja dva vrha u, v \in V. Vrhovi u, v grafa G se još nazivaju krajevima brida e (vidi [1]).

Šetnja u grafu G je konačan niz incidentnih vrhova i bridova. Vrhovi i bridovi u šetnji ne moraju nužno biti i različiti.

Šetnja u kojoj su svi vrhovi i bridovi različiti zove se put. Primjer jednog puta u grafu sa Slike 1 je P = v_{1}\, e_{1}\, v_{2}\, e_{3}\, v_{4}\, e_{6}\, v_{5}\, e_{7}\, v_{6}.

Graf prikazan na Slici 1 nazivamo i neusmjerenim grafom zato što je bridovima grafa moguće prolaziti u oba smjera.

Usmjereni brid zovemo lukom, a ukoliko se svi bridovi grafa orijentiraju (usmjere), tada graf zovemo usmjerenim grafom. Lukovima usmjerenog grafa moguće je prolaziti samo u smjeru orijentacije.

Pridružimo li svakom bridu nenegativan realan broj w(e), dobiveni graf naziva se težinski graf, a broj pridružen bridu e težina brida w(e).

Težinski graf kojem su svi bridovi usmjereni zovemo težinski usmjerenim grafom.

Težinu puta P u grafu G možemo definirati formulom

w(P)= \sum_{e \in {E} (P)} w(e).

Drugim riječima, težina puta P u grafu G je zbroj težina svih bridova kojima se prolazi od početnog do završnog vrha puta P. Tako bi težina puta P = v_{1} \, e_{1}\, v_{2}\, e_{3} \, v_{4}\, e_{6}\, v_{5}\, e_{7}\, v_{6} u grafu sa Slike 1 (uzimajući u obzir težine dane na Slici 2) iznosila 10, dok je istovremeno težina puta Q=v_{1}\, e_{1}\, v_{2}\, e_{4}\, v_{5}\, e_{7}\, v_{6} u grafu sa iste slike 9.

Ukoliko nam je cilj što razumnije koristiti resurse, bilo da se radi o udaljenosti koju trebaju proći automobilom ili vremenu potrebnom za prijenos informacija, htjeli bismo da težina puta između dva vrha bude najmanja moguća. Problem pronalaska takvog puta zovemo problemom najkraćeg puta, a rješenje problema dano je algoritmom koji nazivamo Floyd-Warshallov algoritam.

4Floyd-Warshallov algoritam u tropskoj geometriji

Floyd-Warshallov algoritam je algoritam za pronalaženje najkraćeg puta između bilo koja dva povezana vrha u težinskom grafu.

Obzirom da se računanje svodi na uzastopne transformacije matrica, prednost ovog algoritma je što kod izvršavanja na računalu ne troši velike memorijske resurse.

U nastavku ćemo pojasniti korake algoritma. Odabere se prvi vrh te se redom izračunavaju udaljenosti od tog vrha do svih preostalih vrhova s kojima je on povezan. Ukoliko je promatrani vrh s nekim drugim vrhom povezan s više puteva, tada se za udaljenost između ta dva vrha uzima najmanja udaljenost između ta dva vrha. Ponavljanjem istog postupka za svaki od preostalih vrhova dobiju se najkraće udaljenosti između vrhova u grafu.

Pseudokod Floyd-Warshallovog algoritma

ulaz: Težinski graf G = (V, E), V = v_{1}, v_{2},\ldots, v_{n}
izlaz: Najkraće udaljenosti između svaka dva vrha u grafu G

(1)

Za i = 1, \ldots, n stavi d(i, i) = 0. Za i \ne j, ako je v_{i}v_{j} brid, stavi d(i, j) =w(v_{i}v_{j}), inače stavi d(i, j) = \infty.

(2)

Za k = 1, \ldots, n

\bullet	za i, j = 1, \ldots, n
\bullet	d(i, j) := d(i, j) \oplus \left( d(i, k) \odot d(k, j) \right)

Kada bismo usporedili prikazani pseudokod s klasičnim, zaključili bismo da su samo uobičajene operacije minimuma i zbrajanja zamijenjene tropskim zbrajanjem i množenjem.

No snaga primjene tropske geometrije u ovom slučaju je puno veća. U nastavku ćemo pokazati da se traženje najkraćeg puta u težinskom grafu uz pomoć tropske geometrije svodi na tropsko množenje matrica.

Svakom težinskom grafu možemo pridružiti matricu susjedstva na sljedeći način

D_{(i,j)} =\begin{cases} w(v_{i},v_{j}), & \text{ako su} v_{i} \text{ i } v_{j} \text{ susjedni}\\ 0 ,& \text{ako je}\, i=j \\ \infty, & \text{ako } v_{i} \text{ i } v_{j} \text{ nisu susjedni.} \end{cases}

Primjer 9. Matrica susjedstva grafa sa Slike 2

D=\begin{pmatrix} 0 & 2 & 3 & \infty & \infty & \infty \\ \infty & 0 & \infty & 5 & 6 & \infty \\ \infty & \infty & 0 & \infty & \infty & 8 \\ \infty & \infty & \infty & 0 & 2 & \infty \\ \infty & \infty & \infty & \infty & 0 & 1 \\ \infty & \infty & \infty & \infty & \infty & 0 \end{pmatrix}.

Također, za proizvoljnu kvadratnu matricu, u tropskoj se geometriji definira k-ta tropska potencija matrice kao tropski umnožak k matrica

D^{\odot k}:=\underbrace{D \odot D \odot \cdots \odot D}_{k \ \text{puta}}.

Teorem 1. Neka je G težinski usmjeren graf s n vrhova i n \times n matricom susjedstva D. Tada je element matrice D^{\odot n-1} na poziciji (i,j) jednak duljini najkraćeg puta od vrha v_{i} do vrha v_{j}.

Dokaz. Neka je s d_{ij}^{(r)} označena minimalna duljina bilo kojeg puta od vrha v_{i} do vrha v_{j} koji prolazi kroz najviše r bridova u grafu G.

Neka je d_{ij}^{(1)} = d_{ij} za bilo koja dva vrha v_{i} i v_{j}. Pretpostavivši da su težine bridova nenegativne vrijednosti, najkraći put od v_{i} do v_{j} prolazi najviše jednom kroz svaki vrh u grafu G. Općenito, bilo koji najkraći put u težinski usmjerenom grafu G prelazi kroz najviše n-1 usmjerenih bridova. Otuda slijedi da je duljina najkraćeg puta od vrha v_{i} do vrha v_{j} jednaka d_{ij}^{(n-1)}.

Za r\geq 2 imamo sljedeću rekurzivnu formulu za duljinu najkraćeg puta

(3)

d_{ij}^{(r)} = \min \left\lbrace d_{ik}^{(r-1)} + d_{kj} \ : k = 1, 2,\ldots, n \right\rbrace .

Korištenjem tropske aritmetike prethodna formula može se zapisati na sljedeći način

\begin{eqnarray*} d_{ij}^{(r)}&=& d_{i1}^{(r-1)} \odot d_{1j} \oplus d_{i2}^{(r-1)} \odot d_{2j} \oplus ... \oplus d_{in}^{(r-1)} \odot d_{nj} \\ &=& (d_{i1}^{(r-1)}, d_{i2}^{(r-1)}, \ldots, d_{in}^{(r-1)}) \odot (d_{1j}, d_{2j}, \ldots, d_{nj})^{T}. \end{eqnarray*}

Iz navedenog proizlazi da se d_{ij}^{(r)} podudara sa elementom u i-tom retku i j-tom stupcu matrice D^{\odot r}. Očito je desna strana rekurzivne formula tropski produkt i-tog retka matrice D^{\odot r-1} i j-tog stupca matrice D. Indukcijom po r zaključujemo da se d_{ij}^{(n-1)} podudara s elementom u i-tom retku i j-tom stupcu matrice D^{\odot n-1}

\ \blacksquare

Primjer 10. Računanje elementa matrice D na poziciji (1,4)

\begin{eqnarray*} d^{(1)}_{1,4} &=& ( 0 \odot \infty ) \oplus (2 \odot 5) \oplus (3 \odot \infty) \oplus (\infty \odot 0) \oplus (\infty \odot \infty) \oplus (\infty \odot \infty) \\ &=& \infty \ \oplus \ 7 \oplus \ \infty \ \oplus \ \infty \ \oplus \ \infty \ \oplus \ \infty \\ &=& \min \left\lbrace { \infty, 7, \infty, \infty, \infty, \infty} \right\rbrace \\ &=& 7. \end{eqnarray*}

Primjer 11. Matrica najkraćih puteva grafa sa Slike 2

D^{\odot 5}=\begin{pmatrix} 0 & 2 & 3 & 7 & 8 & 9 \\ \infty & 0 & \infty & 5 & 6 & 7\\ \infty & \infty & 0 & \infty & \infty & 8 \\ \infty & \infty & \infty & 0 & 2 & 3 \\ \infty & \infty & \infty & \infty & 0 & 1 \\ \infty & \infty & \infty & \infty & \infty & 0 \end{pmatrix}.

Navedena matrica predstavlja rješenje problema i iz nje se mogu iščitati najkraće udaljenosti između bilo koja dva povezan vrha.

Slijedi da je d(v_{1},v_{2})=2, d(v_{1},v_{3})=3, d(v_{1},v_{4})=7, d(v_{1},v_{5})=8, d(v_{1},v_{6})=9, d(v_{2},v_{4})=5, d(v_{2},v_{5})=6, d(v_{2},v_{6})=7, d(v_{3},v_{6})=8, d(v_{4},v_{5})=2, d(v_{4},v_{6})=3 i d(v_{5},v_{6})=1.

Napomena 12. Primijetite da iako smo pomoću Floyd-Warshallovog algoritma odredili najkraće udaljenosti između vrhova, algoritam ne otkriva putove kojima su najmanje udaljenosti ostvarene.

Primjer 13. Matrica susjedstva težinski neusmjerenog grafa

Zamislimo li da je graf sa Slike 2 težinski neusmjereni graf, tada bi njegova matrica susjedstva bila sljedeća simetrična matrica

\bar{D}=\begin{pmatrix} 0 & 2 & 3 & \infty & \infty & \infty \\ 2 & 0 & \infty & 5 & 6 & \infty \\ 3 & \infty & 0 & \infty & \infty & 8 \\ \infty & 5 & \infty & 0 & 2 & \infty \\ \infty & 6 & \infty & 2 & 0 & 1 \\ \infty & \infty & 8 & \infty & 1 & 0 \end{pmatrix}.

Izračunavanjem pete potencije matrice susjedstva \bar{D} možemo odrediti simetričnu matricu najkraćih putova težinski neusmjerenog analogona grafa sa Slike 2.

\bar{D}^{\odot 5}=\begin{pmatrix} 0 & 2 & 3 & 7 & 8 & 9 \\ 2 & 0 & 5 & 5 & 6 & 7\\ 3 & 5 & 0 & 10 & 9 & 8 \\ 7 & 5 & 10 & 0 & 2 & 3 \\ 8 & 6 & 9 & 2 & 0 & 1 \\ 9 & 7 & 8 & 3 & 1 & 0 \end{pmatrix}

Bibliografija

[1]	Divjak B., Lovrenčić A. Diskretna matematika s teorijom grafova, FOI-TIVA, Varaždin, 2005.
[2]	Maclagan D., Sturmfels B., Introduction to Tropical Geometry, AMS Grad Stud in Math Vol 161, 2015.
[3]	Speyer D., Sturmfels B., Tropical mathematics, Math Magazine 82 (3), 2009, 163–173.

Boroj 30

Poštovani čitatelji,

izašao je 30 broj časopisa e.math. U ovom broju donosimo članke O zlatnom trokutu, Uparena optimizacijska metoda i CS-dekompozicija J-ortogonalnih matrica malog reda.

U članku O zlatnom trokutu autori Mirela Katić Žlepalo i Bojan Kovačić s Tehničkog veleučilišta Zagreb uvode pojam zlatnog trokuta, te prikazuju geometrijske konstrukcije vezane uz zlatni trokut koje se mogu izvesti ravnalom i šestarom. Članak je od posebnog interesa za metodičare matematike. U članku Uparena optimizacijska metoda, autori Luka Borozan, Slobodan Jelić, Domagoj Matijević, Domagoj Ševerdija sa Sveučilišta J.J. Strossmayera u Osijeku, Odjela za matematiku daju prikaz metoda gradijentnog i zrcalonog spusta u konveksnoj optimizaciji. Temeljem izloženh osnovnih svojstava metoda autori diskutiraju njihoev prednosti i mane i predlažu uparenu - hibridnu - metodu koja kombinacijom pristupa daje robustniji algoritam. Konačno, u članku CS-dekompozicija J-ortogonalnih matrica malog reda autora Vjeran Harija i Vide Zadelj-Martić prezentira se konstruktivna metoda (kombinacijom elementarnih hiperbolnih rotacija i refleksija) konstrukcije dijagonalizacijske matrice (matrice vlastitih vektora) dane indefinitne hermitske matrice. Također, autori daju prikaz algeberskih tehnika kojima se može analizirati odnos dva potprostora u prostorima s indefinitnom metrikom. Ovi rezultati vrijede općenito, no zbog smanjivanja tehničke zahtijevnosti prezentacije, koje ne bi bitno doprinjele razumijevanju tremeljnih koncepeata, autori daju prikaz ključnih tehnika sa svim detaljima na malim primjerim. Također, kratki diskutiraju veze ovakvog pristupa rješavanju indefinitnog simetričnog problema vlastitih vrijednosti u modernom softveru. Ovaj broj tako daje prikaz tehnika vezanih uz osnovne geometrijska preslikavanja (rotacije i zrcaljenja) iz tri različita kuta. MEtodičkog, optimizacijskom i kuta matrične analize.

Na kraju, koristim ovu priliku zaželjeti svim čitateljima časopisa sve najbolje u nadolazećoj godini.

Luka Grubišić

Formule za udaljenost točke do pravca u ravnini, u smislu lp - udaljenosti, 1 ≤ p ≤ ∞.

Aleksandra Jovičić
diplomantica Odjela za matematiku,
Sveučilišta J.J.Strossmayera u Osijeku,
Trg Ljudevita Gaja 6, 31000 Osijek

Kristian Sabo
Odjel za matematiku,
Sveučilište J.J.Strossmayera u Osijeku,
Trg Ljudevita Gaja 6, 31000 Osijek
ksabo@mathos.hr

Sažetak.

Formula za euklidsku udaljenost točke do pravca u ravnini dobro je poznata učenicima završnih razreda srednjih škola. U ovom radu promatramo općenitije probleme udaljenosti točke do pravca u ravnini, u smislu l_{p}-udaljenosti, 1\leq p\leq \infty. Pokazat ćemo da se i u tim slučajevima, također, mogu izvesti analogne formule za računanje udaljenosti točke do pravca.

Zahvala.

Rad je proizašao iz Diplomskog rada: “p-norme na \mathbb{R}^{n} i problemi linearne aproksimacije” autorice Aleksandre Jovičić diplomantice Sveučilišnog nastavničkog studija matematike i informatike na Odjelu za matematiku Sveučilišta J.J.Strossmayera u Osijeku.

Klučne riječi.

Funkcija udaljenosti, Udaljenost točke do pravca, l_{p}-udaljenost, Optimizacija.

1Euklidska udaljenost točke do pravca u ravnini

Ako su A=(x_{1},y_{1}) te B=(x_{2},y_{2}) dvije točke u ravnini \mathbb{R}^{2}, onda

d_{2}(A,B)=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}

zovemo euklidska udaljenost točaka A i B. Nije teško pokazati (vidi, primjerice, [3], [4]) da euklidska udaljenost zadovoljava sljedeća svojstva

\bullet	[(i)] d_{2}(A,B)\geq 0 za svake dvije točke A i B iz \mathbb{R}^{2},
\bullet	[(ii)] d_{2}(A,B)=0 onda i samo onda ako je A=B,
\bullet	[(iii)] d_{2}(A,B)=d_{2}(B,A) za svake dvije točke A i B iz \mathbb{R}^{2},
\bullet	[(iv)] d_{2}(A,C)+d_{2}(C,B)\geq d_{2}(A,B) za svake tri točke A,B i C iz \mathbb{R}^{2}.

Općenito, svaku funkciju d:\mathbb{R}^{2}\times \mathbb{R}^{2}\to[0,\infty\rangle koja ima svojstva (i)-(iv) zovemo funkcija udaljenosti na \mathbb{R}^{2} (vidi, primjerice [5]). Treba reći da se funkcija udaljenosti općenito definira na proizvoljnom nepraznom skupu, no zbog prirode našeg problema, ovdje ćemo se zadržati na skupu \mathbb{R}^{2}.

Pretpostavimo da su u pravokutnom koordinatnom sustavu zadani točka T_{0}=(x_{0},y_{0}) te pravac \pi s jednadžbom y=k\,x+l, k,l\in\mathbb{R}. Još iz srednjoškolske matematike poznato je da se euklidska udaljenost d_{2}(T_{0},\pi) točke T_{0} do pravca \pi računa po formuli

(1)

d_{2}(T_{0},\pi)=\frac{|k x_{0}+l-y_{0}|}{\sqrt{k^{2}+1}}.

Formula (1) može se izvesti na nekoliko načina primjenom geometrijskih ili algebarskih pristupa. Jedan od mogućih izvoda je svođenje na optimizacijski problem. U tu svrhu podsjetimo se kako euklidsku udaljenost d_{2}(T_{0},\pi) točke T_{0} do pravca \pi definiramo kao euklidsku udaljenost točke T_{0} i one točke na pravcu \pi koja je u smislu euklidske udaljenosti najbliža točki T_{0}. Ako je T=(x,y) proizvoljna točka na pravcu \pi, onda euklidska udaljenost točaka T i T_{0} glasi

d_{2}(T_{0},T)=\sqrt{(x-x_{0})^{2}+(y-y_{0})^{2}}=\sqrt{(x-x_{0})^{2}+(k\,x+l-y_{0})^{2}},

te je prema tome

d_{2}(T_{0},\pi)=\min_{x\in\mathbb{R}}\sqrt{(x-x_{0})^{2}+(k\,x+l-y_{0})^{2}}.

To znači da se problem svodi na minimizaciju funkcije

x\mapsto \sqrt{(x-x_{0})^{2}+(k\,x+l-y_{0})^{2}}.

Primijetimo da je umjesto prethodne funkcije dovoljno minimizirati funkciju \varphi_{2} zadanu s

\varphi_{2}(x)=(x-x_{0})^{2}+(k\,x+l-y_{0})^{2}.

Kako je \varphi_{2} kvadratna funkcija, njezin globalni minimum se postiže u apscisi tjemena odgovarajuće parabole, koju ćemo označiti s \xi_{2} te je

\xi_{2}=\frac{k\,y_{0}+x_{0}-k\,l}{k^{2}+1},

odakle iz d_{2}(T_{0},\pi)=\sqrt{\varphi_{2}(\xi_{2})}, nakon kraćeg računa dobivamo da je

d_{2}(T_{0},\pi)=\displaystyle\frac{|k\,x_{0}+l-y_{0}|}{\sqrt{k^{2}+1}}.

Točku (\xi_{2}, k\,\xi_{2}+l) na pravcu \pi koja je u smislu euklidske udaljenosti najbliža točki T_{0} zovemo ortogonalna projekcija točke T_{0} na pravac \pi. Ortogonalna projekcija točke na pravac u ovom je slučaju, očigledno, jedinstvena.

Osim euklidske udaljenosti, moguće je, također, analizirati problem određivanja udaljenosti točke do pravca i u smislu nekih drugih funkcija udaljenosti. U ovom radu promatramo jednu klasu funkcija udaljenosti koje su poznate kao l_{p}-udaljenosti, 1\leq p\leq\infty. Spomenimo da je euklidska udaljenost specijalni slučaj l_{p}-udaljenosti za p=2. Pokazat ćemo da se za svaku od l_{p}-udaljenosti, 1\leq p\leq\infty, također, mogu izvesti lijepe zatvorene formule za udaljenost točke do pravca. Tehnike koje ćemo pri tome koristiti zahtijevaju samo poznavanje osnovnih tvrdnji Diferencijalnog računa funkcije jedne varijable. Kao motivacija za pripremu ovog rada poslužio je članak [2] u kojem se promatra opći slučaj l_{p}-udaljenosti, 1\leq p\leq\infty točke do hiperravnine u \mathbb{R}^{n}.

2l_{p}-udaljenosti, 1\leq p\leq\infty

Ako su A=(x_{1},y_{1}) i B=(x_{2},y_{2}), onda {l_{p}-udaljenost, 1\leq p\leq \infty,} točaka A i B definiramo na sljedeći način

d_{p}(A,B)=\left\lbrace \begin{array}{ll} \left(|x_{1}-x_{2}|^{p}+|y_{1}-y_{2}|^{p}\right)^{1/p},&1\leq p\lt \infty,\\ \max\lbrace |x_{1}-x_{2}|,|y_{1}-y_{2}|\rbrace ,&p=\infty. \end{array}\right.

Primijetimo da za p=2 dobivamo euklidsku udaljenost. Može se pokazati da svaka od l_{p}-udaljenosti, 1\leq p\leq\infty, zadovoljava uvjete (i)-(iv) iz prvog odjeljka te su one, sukladno tome, funkcije udaljenosti (vidi [4]).

Potpuno analogno kao i u slučaju euklidske udaljenosti, l_{p}-udaljenost d_{p}(T_{0},\pi) točke T_{0} do pravca \pi definiramo na sljedeći način

d_{p}(T_{0},\pi)=\min_{x\in\mathbb{R}}\left(|k x+l-y_{0}|^{p}+|x-x_{0}|^{p}\right)^{1/p},\quad 1\leq p\lt \infty,

d_{\infty}(T_{0},\pi)=\min_{x\in\mathbb{R}}\max\lbrace |k x+l-y_{0}|,|x-x_{0}|\rbrace .

Gledano geometrijski, udaljenost točke T_{0} do pravca \pi možemo interpretirati na sljedeći način. Pretpostavimo da smo nacrtali {l_{p}-kružnicu}, 1\leq p \leq \infty (vidi primjerice [1]):

S_{p}(T_{0},\varepsilon)=\lbrace T\in\mathbb{R}^{2}:d_{p}(T,T_{0})=\varepsilon\rbrace ,

sa središtem u točki T_{0} malenog polumjera \varepsilon\gt 0. Napuhujemo li kružnicu S_{p}(T_{0},\varepsilon), 1\leq p\leq \infty, ona će u jednom trenutku za neki \varepsilon_{p}\gt 0 dotaknuti pravac \pi. Polumjer tako dobivene kružnice S_{p}(T_{0},\varepsilon_{p}), 1\leq p\leq \infty, očigledno predstavlja l_{p}- udaljenost točke T_{0} do pravca \pi (vidi Sliku 1). Pri tome točku (\xi_{p},\eta_{p}) na pravcu \pi koja je u smislu l_{p}-udaljenosti najbliža točki T_{0} zovemo {l_{p}-projekcija} točke T_{0} na pravac \pi. Sa Slike 1 odmah je jasno da l_{1} i l_{\infty}-projekcije točke na pravac općenito nisu jedinstvene. Spomenimo da su za sve ostale p, 1\lt p\lt \infty, pripadne l_{p}-projekcije jedinstvene.

Slika 1: Točka T_{0}, pravac \pi i kružnice S_{p}(T_{0},\varepsilon),\,p=1,2,\infty

3l_{1}-udaljenost točke do pravca

Iz tehničkih razloga u ovom odjeljku posebno ćemo izvesti formulu za slučaj l_{1}-udaljenosti. Neka su, kao i dosada, zadani točka T_{0}=(x_{0},y_{0}) te pravac y=k\,x+l. Pri tome u izvodu razlikujemo dvije različite mogućnosti: k=0 te k\neq 0.

Ako je k=0, onda funkcija x\mapsto |l-y_{0}|+|x-x_{0}| postiže globalni minimum u točki x=x_{0}, te je

(2)

d_{1}(T_{0},\pi)=|l-y_{0}|.

Pretpostavimo da je k\neq 0. Funkcija

(3)

x\mapsto |k x+l-y_{0}|+|x-x_{0}|,

je omeđena odozdo te je

\lim_{x\to\infty} \left(|k x+l-y_{0}|+|x-x_{0}|\right)=\lim_{x\to-\infty}\left( |k x+l-y_{0}|+|x-x_{0}|\right)=\infty,

pa postoji točka iz \mathbb{R} u kojoj se postiže njezin globalni minimum. Nadalje, funkcija (3) je po dijelovima linearna te nije derivabilna u točkama \frac{y_{0}-l}{k} i x_{0} te se globalni minimum funkcije (3) postiže u jednoj od tih dviju točaka.

Očigledno je

(4)

\begin{eqnarray} d_{1}(T_{0},\pi)&=&\min\left\lbrace |k x_{0}+l-y_{0}|,\left|\frac{y_{0}-l}{k}-x_{0}\right|\right\rbrace \\ \nonumber &=&\min\left\lbrace |k x_{0}+l-y_{0}|,\frac{|k x_{0}+l-y_{0}|}{|k|}\right\rbrace \\ &=& \frac{|k x_{0}+l-y_{0}|}{\max\lbrace |k|,1\rbrace }.\end{eqnarray}

Konačno iz formula (2) i (4) dobivamo da je

d_{1}(T_{0},\pi)=\displaystyle\frac{|k x_{0}+l-y_{0}|}{\max\lbrace |k|,1\rbrace }.

Označimo s (\xi_{1},\eta_{1})l_{1}-projekciju točke T_{0} na pravac \pi. Uočimo da se za |k|\gt 1 minimum funkcije (3) postiže u x=\frac{y_{0}-l}{k}, dok se za |k|\lt 1 minimum funkcije (3) postiže u x=x_{0}.

Očito je

(5)

\xi_{1}=\left\lbrace \begin{array}{ll}\frac{y_{0}-l}{k},& |k|\gt 1,\\ x_{0},& |k|\lt 1,\end{array}\right.,\quad \eta_{1}=k\,\xi_{1}+l=\left\lbrace \begin{array}{ll}y_{0},& |k|\gt 1,\\ k\,x_{0}+l,& |k|\lt 1.\end{array}\right.

Pokažimo da se u slučaju |k|=1 minimum funkcije (3) postiže u bilo kojoj konveksnoj kombinaciji brojeva \frac{y_{0}-l}{k} i x_{0}, tj. za svaki

(6)

\xi_{1}(\lambda)=\lambda \frac{y_{0}-l}{k}+(1-\lambda) x_{0},\quad \lambda\in [0,1].

Zaista, za |k|=1 te \lambda\in[0,1] imamo

\begin{eqnarray} \left|k\,\xi_{1}(\lambda)+l-y_{0}\right|+\left|\xi_{1}(\lambda)-x_{0}\right|&=&\left|k \left(\lambda \frac{y_{0}-l}{k}+(1-\lambda) x_{0}\right)+l-y_{0}\right|\\ &+&\left|\lambda \frac{y_{0}-l}{k}+(1-\lambda) x_{0}-x_{0}\right|\\ \nonumber &=&(1-\lambda)|k x_{0}+l-y_{0}|+\lambda |k x_{0}+l-y_{0}|\\ \nonumber &=& |k x_{0}-l-y_{0}|\\ \nonumber &=& d_{1}(T_{0},\pi).\end{eqnarray}

Zaključujemo kako je u slučaju |k|\neq 1, l_{1}-projekcija točke T_{0} na pravac \pi jedinstvena točka (\xi_{1},\eta_{1}) zadana s (5), dok je u slučaju |k|=1 svaka točka oblika (\xi_{1}(\lambda),k\,\xi_{1}(\lambda)+l-y_{0}), \lambda\in[0,1], l_{1}-projekcija točke T_{0} na pravac \pi, pri čemu je \xi_{1}(\lambda) zadan sa (6).

4l_{p}-udaljenost, 1\lt p\lt \infty, točke do pravca

U ovom općem slučaju problem se svodi na minimizaciju funkcije

x\mapsto \left(|k x+l-y_{0}|^{p}+|x-x_{0}|^{p}\right)^{1/p},\quad 1\lt p\lt \infty.

Slično kao kod euklidske udaljenosti dovoljno je minimizirati funkciju

\varphi_{p}(x)=|k x+l-y_{0}|^{p}+|x-x_{0}|^{p}, \quad 1\lt p\lt \infty.

Kako je funkcija \varphi_{p} omeđena odozdo te je

\lim_{x\to\infty}\left( |k x+l-y_{0}|^{p}+|x-x_{0}|^{p}\right)=\lim_{x\to-\infty}\left( |k x+l-y_{0}|^{p}+|x-x_{0}|^{p} \right)=\infty,

postoji točka iz \mathbb{R} u kojoj se postiže njezin globalni minimum. S ciljem određivanja te točke, posebno promatramo dva slučaja: k=0 te k\neq 0.

Ako je k=0, onda je \varphi_{p}(x)=|l-y_{0}|^{p}+|x-x_{0}|^{p}, te se njezin minimum postiže u točki x=x_{0} pa je

(7)

d_{p}(T_{0},\pi)=|l-y_{0}|.

Neka je k\neq 0. Primijetimo da je funkcija \varphi_{p} derivabilna u svim točkama na \mathbb{R} osim možda u točkama x=x_{0} te x=\frac{y_{0}-l}{k} te ćemo u svrhu minimizacije funkcije \varphi_{p} upotrijebiti znanja iz Diferencijalnog računa funkcije jedne varijable.

Promatrajmo funkciju \varphi_{p} na skupu \mathbb{R}\setminus\left\lbrace x_{0},\frac{y_{0}-l}{k}\right\rbrace. Bez smanjenja općenitosti pretpostavimo da je x_{0}\lt \frac{y_{0}-l}{k} (slučaj x_{0}\geq \frac{y_{0}-l}{k} može se analizirati potpuno analogno).

Pokažimo najprije da funkcija \varphi_{p} nema stacionarnih točaka na intervalima \langle -\infty,x_{0}\rangle te \langle \frac{y_{0}-l}{k},+\infty\rangle.

Ako je x\in\langle -\infty, x_{0}\rangle, funkcija \varphi_{p} je derivabilna u x te je

\begin{eqnarray} \frac{d\varphi_{p}(x)}{dx}&=&|k|^{p} p\left|x-\frac{y_{0}-l}{k}\right|^{p-1}\text{sign}\left(x-\frac{y_{0}-l}{k}\right)+p |x-x_{0}|^{p-1}\text{sign}(x-x_{0})\\ \nonumber &=&-|k|^{p} p\left|x-\frac{y_{0}-l}{k}\right|^{p-1}-p |x-x_{0}|^{p-1}\lt 0,\end{eqnarray}

gdje je \text{sign}(x)=\left\lbrace \begin{array}{rl} 1,& x\gt 0\\ 0,& x=0\\ -1,&x\lt 0, \end{array}\right. tzv. funkcija predznaka.

Ako je x\in\langle \frac{y_{0}-l}{k},+\infty\rangle, funkcija \varphi_{p} je derivabilna u x te je

\begin{eqnarray} \frac{d\varphi_{p}(x)}{dx}&=&|k|^{p} p\left|x-\frac{y_{0}-l}{k}\right|^{p-1}+p |x-x_{0}|^{p-1}\gt 0.\end{eqnarray}

Preostaje analizirati slučaj x\in\langle x_{0},\frac{y_{0}-l}{k}\rangle. Na tom je skupu funkcija \varphi_{p} također derivabilna te je

(8)

\begin{eqnarray} \frac{d\varphi_{p}(x)}{dx}&=&-|k|^{p} p\left|x-\frac{y_{0}-l}{k}\right|^{p-1}+p |x-x_{0}|^{p-1}.\end{eqnarray}

Rješenje jednadžbe \frac{d\varphi_{p}(x)}{dx}=0, glasi

(9)

\xi_{p}=\frac{1}{|k|^{\frac{p}{p-1}}+1}x_{0}+\frac{|k|^{\frac{p}{p-1}}}{|k|^{\frac{p}{p-1}}+1}\frac{y_{0}-l}{k}.

Uočimo da je \xi_{p}\in\langle x_{0},\frac{y_{0}-l}{k}\rangle te

\varphi_{p}(\xi_{p})=\left(\displaystyle\frac{|k x_{0}+l-y_{0}|}{\left(|k|^{\frac{p}{p-1}}+1\right)^{\frac{p-1}{p}}}\right)^{p}.

Kandidati za točku u kojoj se postiže globalni minimum funkcije \varphi_{p} su x_{0}, \frac{y_{0}-l}{k} te \xi_{p} zadana s (9). Pokažimo da je

\min\left\lbrace \varphi_{p}(x_{0}),\varphi_{p}\left(\frac{y_{0}-l}{k}\right),\varphi_{p}(\xi_{p})\right\rbrace =\varphi_{p}(\xi_{p}).

U tu svrhu uočimo da za svaki 1\lt p\lt \infty i svaki k\in\mathbb{R} vrijedi

(10)

\left(|k|^{\frac{p}{p-1}}+1\right)^{\frac{p-1}{p}}\gt |k|,

(11)

\left(|k|^{\frac{p}{p-1}}+1\right)^{\frac{p-1}{p}}\gt 1.

Prema (10) i (11) imamo

\min\left\lbrace \left(\frac{|k x_{0}+l-y_{0}|}{|k|}\right)^{p},\left|k x_{0}+l-y_{0}\right|^{p},\left(\frac{|k x_{0}+l-y_{0}|}{\left(|k|^{\frac{p}{p-1}}+1\right)^{\frac{p-1}{p}}}\right)^{p}\right\rbrace =\left(\frac{|k x_{0}+l-y_{0}|}{\left(|k|^{\frac{p}{p-1}}+1\right)^{\frac{p-1}{p}}}\right)^{p}.

Konačno slijedi da je d_{p}(T_{0},\pi)=\left(\varphi(\xi_{p})\right)^{1/p}, odakle je

d_{p}(T_{0},\pi)=\displaystyle\frac{|k x_{0}+l-y_{0}|}{\left(|k|^{\frac{p}{p-1}}+1\right)^{\frac{p-1}{p}}},\quad 1\lt p\lt \infty.

Tablica 1:

Iz izvoda formule (1) neposredno proizlazi da je (\xi_{p},k\,\xi_{p}+l), gdje je \xi_{p} dan s (9) pripadna l_{p}-projekcija točke T_{0} na pravac \pi.

Ako s q\in \mathbb{R} označimo tzv. konjugirani eksponent od p (vidi [3]), odnosno broj sa svojstvom da je \frac{1}{p}+\frac{1}{q}=1, onda formulu (1) možemo zapisati u obliku

d_{p}(T_{0},\pi)=\frac{|k x_{0}+l-y_{0}|}{\left(|k|^{q}+1\right)^{\frac{1}{q}}}= \frac{|k x_{0}+l-y_{0}|}{d_{q}((k,1),(0,0))}.

5l_{\infty}-udaljenost točke do pravca

Ako su T_{0}=(x_{0},y_{0}) te y=k\,x+l, onda je problem određivanja l_{\infty}-udaljenosti ekvivalentan minimizaciji funkcije

\varphi_{\infty}(x)= \max\lbrace |x-x_{0}|,|k\,x+l-y_{0}|\rbrace .

Analogno kao u slučaju funkcije \phi_{p} može se pokazati da postoji točka u kojoj se postiže globalni minimum funkcije \varphi_{\infty}. Funkcija \varphi_{\infty} je konveksna po dijelovima linearna funkcija te iz grafa (vidi Sliku 2) slijedi da se njezin globalni minimum postiže u točki \xi_{\infty} za koju vrijedi

Slika 2: Graf funkcije \phi_\infty za k\ne0.

|\xi_{\infty}-x_{0}|=|k\,\xi_{\infty}+l-y_{0}|.

Ako je |k|\neq 1, ova jednadžba ima dva rješenja

\xi_{\infty,1}=\frac{y_{0}-x_{0}-l}{k-1},\quad \xi_{\infty,2}=\frac{y_{0}-x0-l}{k+1}

te je

\begin{align*} \min \varphi_{\infty}(x)&= \min \lbrace \varphi_{\infty}(\xi_{\infty,1}),\varphi_{\infty}(\xi_{\infty,2})\rbrace \\ &=\min\left\lbrace \frac{|kx_{0}+l-y_{0}|}{|k-1|},\frac{|kx_{0}+l-y_{0}|}{|k+1|}\right\rbrace \\ &=|kx_{0}+l-y_{0}|\min\left\lbrace \frac{1}{|k-1|},\frac{1}{|k+1|}\right\rbrace =\frac{|kx_{0}+l-y_{0}|}{|k|+1}, \end{align*}

pri čemu je posljednja jednakost posljedica identiteta

\min\left\lbrace \frac{1}{|k-1|},\frac{1}{|k+1|}\right\rbrace =\frac{1}{|k|+1},

koji se može lako provjeriti. Slično se može analizirati slučaj |k|=1, te konačno dobivamo formulu

d_{\infty}(T_{0},\pi)=\displaystyle\frac{|k\,x_{0}+l-y_{0}|}{|k|+1}.

Primijetimo, također, da je

d_{\infty}(T_{0},\pi)=\frac{|k\,x_{0}+l-y_{0}|}{d_{1}((k,1),(0,0))}.

Izvod formule za l_{\infty}-projekciju točke T_{0} na pravac \pi ostavljamo zainteresiranim čitateljima.

6Zaključna formula

Na kraju ćemo rezimirati sve prethodno navedene formule. Ako su p,q\in\mathbb{R} konjugirani eksponenti, odnosno, takvi da je \frac{1}{p}+\frac{1}{q}=1 te ako je konjugirani eksponent od p=1 definiramo uobičajeno kao q=\infty, onda l_{p}-udaljenost 1\leq p\leq \infty, d_{p}(T_{0},\pi) točke T_{0} do pravca \pi glasi

d_{p}(T_{0},\pi)=\displaystyle\frac{|k\,x_{0}+l-y_{0}|}{d_{q}((k,1),(0,0))}.

Također, osim u eksplicitnom obliku, pravac \pi možemo promatrati u implicitnom obliku ax+by+c=0. U tom se slučaju može izvesti odgovarajuća formula za udaljenost točke T_{0} do pravca \pi, koja glasi

d_{p}(T_{0},\pi)=\displaystyle\frac{|a\,x_{0}+b\,y_{0}+c|}{d_{q}((a,b),(0,0))},

gdje su p,q\in\mathbb{R} konjugirani eksponenti.

Bibliografija

[1]	Lj. Arambašić, I. Zavišić, p-norme na \mathbb{R}^{2}, kružnice S_{p} i brojevi \pi_{p}, Osječki matematički list, 10(2010), 131-138
[2]	E. Melachrinoudis, An Analytical Solution to the Minimum L_{p}-Norm of a Hyperplane}, Journal of Mathematical Analysis and Applications 211(1997), 172-189
[3]	S. Kurepa, Funkcionalna analiza : elementi teorije operatora, Školska knjiga, Zagreb, 1981.
[4]	S. Mardešić, Matematička analiza, 1. dio, Školska knjiga, Zagreb, 1974.
[5]	Š. Ungar, Matematička analiza u \mathbb{R}^{n}, Golden Marketing - Tehnička knjiga, Zagreb, 2005.

27. broj časopisa e.math

Dragi čitatelji,

izašao je 27 broj časopisa e.math.

U ovom broju donosimo vam članke vezane uz teoriju grafova, heurističku optimizaciju i genetske algoritme te metodički članak o nastavnom pristupu čunjosječnicama.

U članku Genetski algoritmi i biomorfi, autora Tomislava Droždjeka i Nele Bosner daje se prikaz evolucijskih algoritama kao vrste heurističkih optimizacijskih algoritama koji su projektirani oponašanjem prirodnih procesa (u ovom slučaju procesom evolucije). Istaknimo da je po rječničkoj definiciji heuristički postupak onaj u kojem se znanstveno rješenje traži metodom pokušaja i pogrešaka. U slučaju optimizacije to znači da nećemo rigorozno dokazivati da je pronađeno rješenje (izlaz iz algoritma) optimalno, već ćemo se zadovoljiti time da izlaz iz algoritma ima bolja svojstva (mjera kojih je funkcija cilja) od ulaza (početnog stanja) u algoritam. Evolucijski algoritmi su područje istraživanja računarstva, a ovaj članak može služiti kao izvrsna referenca studentima matematike i računarstva za kolegij Umjetna inteligencija. Pdf verziju članka možete naći na portalu Hrcak.

U članku Petersenov graf, autora Snježane Majstorović i Luke Borasa daje se pregled rezultata vezanih uz Petersonov graf. To je graf s 10 vrhova i 15 bridova koji se pojavljuje kao čest protuprimjer za mnoge probleme u teoriji grafova. Jedno od zanimljivih svojstava Petersonovog grafa je da je to najmanji snark. Istaknimo da je 1946 Danilo Blanuša pronašao dva snarka s 18 vrhova koji su danas poznati kao blanušini snarkovi jedan od kojih je i logo Hrvatskog matematičkog društva. Pdf verziju članka možete naći na portalu Hrčak.

U članku Različiti nastavno-metodički pristupi čunjosječnicama, Ivančice Mirošević, Nikole Koceić-Bilana i Josipe Jurko dan je pregled različitih metodičkih pristupa uvođenju čunjosječnica u nastavu matematike. Članak stavlja naglasak na metodičku vrijednost geometrijskog pristupa konstrukciji i uvođenju čunjosječnica u nastavi matematike. Trenutna metodička praksa gotovo isključico stavlja nastavak na algebarski pristup, čime se propušta prilika senzibiliziranja učenika za otkrivanje i povezivanje svojstava geometrijskih objekata s pojavama koje ga okružuju (npr. korištenje i značaj krivulja drugog reda u arhitekturi, optici ili astronomiji). Vezano uz primjene svojstava krivulja drugog reda u astronomiji istaknimo i Papus-Boškovićev pristup krivuljama drugog reda i s time povezan pojam numeričkog ekscentriciteta elipse. Pdf verziju članka možete naći na portalu Hrčak.

U ime uredništva želim vam ugodno čitanje.

L. Grubišić
glavni urednik

Genetski algoritmi i biomorfi

Nela Bosner (nela.bosner@math.hr ) i Tomislav Droždjek

Genetski algoritmi su jedna vrsta evolucijskih algoritama. Evolucijski algoritmi, kao što i samo ime govori, posebna su vrsta algoritama inspirirana procesom evolucije. Glavna ideja evolucijskih algoritama je, koristeći metodu pokušaja i pogrešaka, simulirati proces evolucije te ga primijeniti na rješavanje raznih optimizacijskih problema. Promotrimo sada podrobnije kako je pojam evolucije povezan s evolucijskim algoritmima. U teoriji evolucije, neku okolinu nastanjuje populacija jedinki kojima je “cilj” preživjeti i razmnožavati se. Podobnost (eng. fitness) tih jedinki govori nam koliko je pojedina jedinka uspješna u ispunjavanju tih ciljeva, odnosno, ona reprezentira šansu jedinke da preživi dovoljno dugo kako bi se razmnožavala. U kontekstu rješavanja problema, jedinke izjednačavamo s kandidatima za rješenje. Kvaliteta tih potencijalnih rješenja nam govori koliko dobro ona aproksimiraju rješenje problema. Nju možemo iskoristiti kako bismo odlučili s kolikom će vjerojatnošću određeni kandidat za rješenje sudjelovati u konstrukciji sljedećih kandidata (intuitivno, što kandidat za rješenje bolje aproksimira rješenje ta bi vjerojatnost trebala biti veća).

1Inspiracija u biologiji

Darwinova teorija evolucije daje nam objašnjenje bioraznolikosti i mehanizama kojima se postiže bioraznolikost. U makroskopskom pogledu na evoluciju, glavnu ulogu igra proces prirodne selekcije. U okolini u kojoj može živjeti samo određen broj jedinki, očito je da je potreban neki oblik selekcije, ako se želi izbjeći eksponencijalan rast populacije. Prirodna selekcija favorizira one jedinke koje su najbolje prilagođene uvjetima okoline, tj. koje najbolje mogu iskoristiti dostupne resurse.

Ovako opisana prirodna selekcija je jedna od dvije osnovne ideje teorije evolucije. Druga osnovna ideja rezultat je fenotipskih varijacija unutar populacije. Fenotip jedinke su karakteristike jedinke (fizičke ili biheviorističke) koje imaju direktan utjecaj na interakciju jednike s okolinom. Odnosno, to su karakteristike koje utječu na njenu podobnost, a preko toga i na vjerojatnost njenog preživljavanja. Svaka jedinka jedinstvena je kombinacija fenotipskih karakteristika. Ako okolina te fenotipske karakteristike ocijeni povoljno, onda se one zadržavaju u populaciji kroz potomstvo te jedinke. S druge strane, negativno ocijenjene karakteristike gube se, jer negativno ocijenjene jedinke češće umiru bez potomstva. Darwin je uočio da se male nasumične varijacije, mutacije, u fenotipu događaju tijekom reprodukcije iz generacije u generaciju. Kao rezultat tih varijacija, pojavljuju se i ocijenjuju nove kombinacije svojstava. Najbolje među njima prežive i razmnožavaju se, i time omogućuju evoluciju.

Ukratko, populacija se sastoji od određenog broja jedinki. Vjerojatnost da se te jedinke razmnožavaju direktno ovisi o tome koliko su one dobro prilagođene okolini. Razmnožavanjem uspješnijih jedinki, uz povremene mutacije, pojavljuju se nove jedinke. Time se, uz dovoljno vremena, mijenja cijela populacija, dakle ona evoluira.

Grafički se taj proces može prikazati kao na slici 1. z-os grafa prikazuje podobnost (fitnes), dakle veći z pridružujemo boljoj podobnosti i obrnuto. x i y os pridružujemo nekim karakteristikama jedinke. Očito, na x–y ravnini sada se nalaze sve moguće kombinacije karakteristika, dok se na z-osi može očitati podobnost jedinke s tim karakteristikama. Neku populaciju sad možemo zamisliti kao skup točaka u prostoru, gdje svaka točka predstavlja jednu jedinku. Evoluciju tada možemo zamisliti kao proces postupnog pomaka populacije na veću visinu. Valja spomenuti da je, zbog konačnog broja jedinki te zbog nasumičnosti u cijelom procesu, moguć gubitak dobro prilagođenih jedinki iz populacije. To nam, za razliku od procesa optimizacije, omogućuje i “pomicanje nizbrdo” te nam ništa ne jamči da će se populacija vratiti istim putem. Iz toga slijedi da je moguće pobjeći iz lokalnih optimuma te postići globalni optimum.

Slika 1: Primjer ovisnosti vrijednosti podobnosti o kombinaciji 2 gena.

2Što je evolucijski algoritam?

Kao što smo već spomenuli u prethodnom poglavlju, ideja na kojoj se baziraju evolucijski algoritmi je da će se opća podobnost populacije podići kao rezultat prirodne selekcije. Polazište evolucijskih algoritama je reprezentacija jedinki. Ona definira vezu izmedu prostora u kojem se nalazi problem i prostora u kojem će evolucijski algoritam tražiti rješenje. Kandidate za rješenje unutar prostora u kojem se nalazi problem zovemo fenotipi, dok njihove reprezentante u algoritmu zovemo genotipi. Za danu funkciju podobnosti koju trebamo maksimizirati, nasumično kreiramo skup kandidata za rješenje te na njih primijenimo funkciju. Na temelju rezultata, možemo odabrati bolje kandidate kao roditelje sljedeće generacije i na njih primijeniti rekombinaciju i/ili mutaciju.

∙

Rekombinacija je binarni operator varijacije (eng. recombination, crossover). Kao što i samo ime govori, ovaj operator spaja genetske informacije dva roditelja u jedan ili više potomaka. Operator rekombinacije je stohastički; izbor dijelova koji će svaki roditelj prenijeti na potomke te način spajanja tih dijelova je nasumičan.

∙

Mutacija je unarni operator varijacije. Ulazni podatak operatora mutacije je jedan genotip, a izlazni je modificirani genotip. Promjena između ta dva genotipa je obično mala. Mutacija je uvijek stohastički operator; genotip potomka je rezultat niza nasumičnih promjena.

Primjenom tih operatora dobijemo novi skup kandidata za rješenje za koje opet izračunamo njihovu podobnost. Nakon toga, novi zajedno sa starim kandidatima ulaze u izbor za kandidate koji će se prenijeti u sljedeću generaciju. Taj izbor najčešće se zasniva na temelju podobnosti, ali se može zasnivati i na temelju starost kandidata. Opisani proces ponavljamo sve dok ne pronađemo dovoljno dobrog kandidata za rješenje.

Dakle, gore navedeni proces zasniva se na dvije stvari:

∙

Operatori mutacije i rekombinacije stvaraju potrebnu raznolikost i time omogućavaju varijacije u populaciji

∙

Funkcija podobnosti omogućuje nam selekciju rješenja.

Kombinacija tih dviju pokretačkih sila vodi do porasta podobnosti kandidata kroz generacije.

Primijetimo da je evolucijski proces stohastički. Iako je vjerojatnost odabira jedinki s višom podobnosti veća od vjerojatnosti odabira jedinki s manjom podobnosti, čak i te manje kvalitetne jedinke imaju pozitivnu vjerojatnost preživljavanja, kao i vjerojatnost da će postati roditelj. Naime, i kod odabira roditelja kod rekombinacije, i kod odabira jedinke za mutaciju, taj odabir se vrši nasumično. Algoritam 1 prikazuje pseudokod evolucijskog algoritma.

Algoritam 1: Evolucijski algoritam

3Genetski algoritmi

Ne postoji jedan način za kreiranje genetskog algoritma; on nastaje kombinacijom različitih raspoloživih operatora tako da bude prikladan za rješavanje nekog konkretnog problema. Ideju genetskog algoritma je inicijalno začeo Holland 1973. godine kao sredstvo proučavanja adaptivnog ponašanja. Oni se u glavnom smatraju optimizacijskim metodama. Klasični genetski algoritam ima binarnu reprezentaciju, selekciju proporcionalnu podobnosti, nisku vjerojatnost mutacije, naglasak na genetski inspiriranoj rekombinaciji, i generacijski izbor kandidata koji će se prenijeti u sljedeću generaciju. Kao što smo već prije spomenuli, prvi korak u konstrukciji bilo kojeg evolucijskog algoritma je određivanje reprezentacije kandidata za rješenje. To uključuje definiciju genotipa te preslikavanja s genotipa u fenotip. Kod genetskih algoritama najčešće se koriste

∙

binarna reprezentacija: genotip prikazan kao string binarnih znamenki,

∙

reprezentacija prirodnim brojevima: genotip prikazan kao string prirodnih ili cijelih brojeva, ili nekog njihovog podskupa,

∙

reprezentacija realnim brojevima: genotip prikazan kao string realnih brojeva,

∙

reprezentacija permutacijama: genotip je prikazan kao permutacija skupa prirodnih brojeva.

4Eksperimenti s biomorfima

Rad genetskih algoritama ilustrirat ćemo primjerima biomorfa, koji su inspirirani pravim biološkim oblicima i njihovom evolucijom. Biomorf je u širem smislu riječi bilo koji objekt koji nalikuje na živo biće. Njih je u računarstvo prvi uveo Richard Dawkins u knjizi “The blind watchmaker”, kako bi pokazao da se gomilanjem malih promjena na genima kroz dovoljno generacija mogu razviti bitno drugačiji organizmi od početnog. U našim eksperimentima biomorfi su dvodimenzionalna “bića” nalik grančicama, koja nastaju uzastopnim grananjem linija na način koji je određen njihovim genima. Slika 3 prikazuje nekoliko tipičnih primjera biomorfa. Eksperimente slične Dawkinsovima pokušat ćemo ponoviti i u ovom članku, kako bismo demonstrirali efikasnost genetskih algoritama, uz bitnu razliku da ćemo podobnost organizama vrednovati nekom funkcijom podobnosti, dok je Dawkins u originalnom radu sam birao organizme koji će biti roditelji sljedeće generacije na temelju njihovog izgleda. Konkretno, pokrenut ćemo neki genetski algoritam na različitim problemima s različitim parametrima te usporediti rezultate.

Slika 3: Neki tipični biomorfi.

Pozabavimo se detaljnije strukturom biomorfa. Biomorfi koje ćemo koristiti u našim pokusima imat će 9 gena. Prvih 8 reprezentirat ćemo cijelim brojevima u rasponu od -8 do 7, dok ćemo deveti gen reprezentirati prirodnim brojevima od 1 do 8. Taj, deveti gen reprezentira broj “nivoa” od kojih će se sastojati određeni biomorf, dok prvih 8 utječe na duljinu i nagib njegovih grana. Konkretno, predznak prvih 8 gena govorit će nam u kojem smjeru vodi određena grana, dok će njihov iznos utjecati na duljinu. Slika 4 prikazuje jedan, relativno jednostavan biomorf u sredini (genotipa [-1,-1,-1,-1,-1,-1,-1,-1,4]), dok su oko njega neki biomorfi nastali mutacijom samo jednog od njegovih gena za +1 ili -1. Svaka grana biomorfa se, kad dođe do kraja, razdvaja na točno dvije nove grane. Duljina grane, osim što ovisi o genima, linearno se smanjuje s brojem grananja od korijena do te grane. Ukoliko se neka od tih grana ne vidi na crtežu, njezina duljina je 0, no još uvijek se iz nje mogu granati nove grane.

Slika 4: Prikaz biomorfa i njemu bliskih biomorfa.

Objasnimo sada malo pobliže proces grananja biomorfa. U trenutku kada grana dođe do svojeg kraja, geni određuju duljinu i kut grananja grana nastalih iz nje. Primijetimo da je prva grana biomorfa usmjerena ravno prema dolje, dakle raste “u smjeru juga”. Grane nastale iz nje tada rastu u smjeru “jugoistoka” i “jugozapada”. Zapravo, ako zamislimo ružu vjetrova s 8 krakova, grananje iz neke grane uvijek će ići “u smjeru” 2 susjedna kraka. Navodnike smo ovdje stavili jer ti smjerovi nisu pravilno rasporedeni kao na ruži vjetrova, bitno je samo da ih ima 8. Kad bi za svaki od tih smjerova jedan gen na neki način određivao pomak u smjeru x, a jedan u smjeru y, očito bi trebali 16 različitih gena. No, primijetimo da su svi biomorfi simetrični s obzirom na y. To nam omogućuje redukciju broja gena na 8. U tablici 1, za svaki smjer ruže vjetrova dan je indeks gena koji na njega utječe u smjeru x i y osi. Smjer 3 je ravno dolje, 7 je ravno gore (zbog toga jer je dx u tim smjerovima jednak 0), dok su ostali smjerovi raspoređeni u smjeru kazaljke na satu.

Tablica 1: Veza gena i rasta biomorfa.

Slika 5: Ruže vjetrova za dva genotipa.

Iako na prvi pogled i nije jasno koliko veliku varijabilnost fenotipa biomorfa možemo dobiti na ovaj način, na slici 6 dano je 6 biomorfa koji su dobiveni jedan od drugog mutacijom samo jednog gena, dakle drugi biomorf dobiven je mutacijom jednog gena iz prvog itd. (Mutacija je ovdje implementirana kao nasumično biranje bilo kojeg n∈[-8,7]). Razlike u fenotipu su drastične, iako je promijenjen samo jedan gen.

Slika 6: Ilustracija promjena na biomorfu nastalih mutacijom jednog gena.

4.1Primjeri

Naše primjere modelirat ćemo genetskim algoritmom sa sljedećim elementima.

∙

Populacija se sastoji od 500 jedinki, nasumično inicjaliziranih.

∙

Mehanizam odabira roditelja je turnirska selekcija (deterministički odabir, biramo λ roditelja). Ovakav mehanizam odabira pogodan je za situacije kad možemo uspoređivati samo koliko je neka strategija dobra u usporedbi s nekom drugom. Turnirska selekcija ne zahtijeva znanje o cijeloj populaciji, dovoljno je imati relaciju koja može usporediti bilo koje 2 jedinke. Pseudokod turnirske selekcije koja odabire λ roditelja dan je sa algoritmom 2. Vjerojatnost odabira jedinke kao pobjednika turnira ovisi o rangu jedinke u populaciji, i o veličini turnira k.

Algoritam 2: Pseudokod za turnirsku selekciju

∙

Mutacija je implementirana kao biranje nasumičnog broja iz [-8,7] za jedan gen u jedinki, pri čemu do mutacije dolazi s vjerojatnošću p.

∙

Rekombinacija je implementirana kao križanje u jednoj točki, a broj nivoa uzimamo nasumično od jednog roditelja. U ovom tipu operatora rekombinacije odabiremo nasumičan broj iz [0,l-1], gdje je l duljina stringa genoma, te nakon toga “presječemo” oba roditelja u toj točci i zamijenimo njihove zadnje dijelove. Time dobijemo dvoje nove djece.

Slika 8: Primjer rekombinacije u jednoj točci.

∙

Odabir preživjelih se obavlja izbacivanjem λ najmanje podobnih jedinki iz populacije.

∙

Uvjet zaustavljanja je zadovoljen kad je postigunt maksimalan broj generacija ili nema nikakvog poboljšanja u podobnosti populacije u 20 generacija.

Geneski algoritam pokrenuti ćemo 100 puta sa svakom kombinacijom parametara te ćemo za svaki od njih, u svakoj generaciji pamtiti najbolju i prosječnu podobnost, kao i genotip najbolje jedinke. Parametri koje smo koristili dani su u tablici 2.

Tablica 2: Parmetri genetskog algoritma

Zamislimo da želimo konstruirati takav biomorf kojem podobnost raste sa svakim slobodnim krajem grane unutar nekog prostora, no za konstrukciju njegovih grana potrebni su resursi, dakle što je suma duljina grana dulja, to je veći negativni efekt na podobnost jedinke (ovdje smo cijenu definirali kao duljinu grane). Možemo zamisliti da se radi o korijenu drva koje raste na tlu u kojem su nejednoliko raspoređene hranjive tvari. Točnije, količina hranjivih tvari linearno raste porastom dubine, do y=-200 nakon čega počne linearno padati. Primijenili smo gore opisani genetski algoritam, koristeći sva 4 seta parametara. Maksimalan broj iteracija stavili smo na 200.

Tablica 3 prikazuje broj pokretanja kod kojih rješenje nije pronađeno te broj dobivenih rješenja koja su različita od najboljeg dobivenog rješenja, kao i odstupanja od najboljeg rješenja.

Tablica 3: Podaci o izvedbi algoritma

Možemo primijetiti da je najbrže nalaženje rješenja kod parametara iz seta 3 zbog najvećeg selekcijskog pritiska, kao i najsporije uz korištenje parametara iz seta 2 zbog najmanjeg broja djece u svakoj generaciji. Zanimljivo je uočiti da odabir prevelikog parametra mutacije negativno utječe na kvalitetu rješenja. No, crtanjem najbolje jedinke ispostavilo se da je algoritam kao optimalno rješenje pronašao okomitu crtu prema dolje (točnije, više crta koje sve putuju ravno prema dolje; svaki pomak po osi x je nepoželjan jer ne nosi nikakvu nagradu, a negativno utječe na podobnost). Slika 9 prikazuje nekoliko biomorfa koji su u jednom pokretanju algoritma bili najbolje rješenje u svojoj generaciji. Promatramo li ih po redu (od gore lijevo prema dolje desno), možemo jasno vidjeti kako se biomorf stanjuje i približava ravnoj okomitoj liniji. Ponovimo sada pokus tako da dodatno nagradimo jedinke koje će imati veći raspon “korijena”.

Slika 9: Neki biomorfi dobiveni u jednom pokretanju algoritma.

Koristit ćemo istu funkciju podobnosti kao i u prethodnom primjeru, no dodat ćemo još jedan pribrojnik koji je proporcionalan najvećoj udaljenosti 2 slobodna kraja grana. Time se nadamo dobiti biomorfe koji se neće grupirati oko samo jedne linije, a ujedno ćemo dodatno zakomplicirati funkciju podobnosti te promotriti kako se naš algoritam nosi s tim. Opet smo algoritam pokrenuli 100 puta sa svakim setom podataka, s maksimalno 200 iteracija. Tablica 4 prikazuje broj pokretanja kod kojih rješenje nije uspješno pronađeno, broj dobivenih rješenja koja su različita od najboljeg dobivenog rješenja te odstupanja od najboljeg rješenja.

Tablica 4: Podaci o izvedbi algoritma

Možemo primijetiti da se prosječno odstupanje od najboljeg rješenja smanjilo, iako se broj suboptimalnih rješenja povećao. Posebno vrijedi istaknuti porast u kvaliteti performansi seta parametara s većim parametrom mutacije. To možemo pripisati strukturi prostora rješenja. U prošlom primjeru velik parametar mutacije onemogućavao je brzo penjanje prema optimalnom rješenju što je usporavalo algoritam i često nas izbacivalo s puta prema tom optimumu; ovdje se to pokazalo korisnim zbog kompleksnije strukture prostora (većeg broja bliskih po podobnosti lokalnih optimuma) te omogućilo skakanje između njih. Međusobni odnos rezultata dobivenih različitim parametrima ostao je vrlo sličan kao i u prethodnom primjeru. Možemo primijetiti da su se performanse algoritma s parametrima iz seta 4 skoro izjednačile s onima iz prvog seta, iako su u jednostavnijem primjeru bile dosta lošije. Set 2 i dalje je najlošiji, dok set 3 daje najbrže nalaženje rješenja, no i nešto lošiju točnost rezultata.

Također, zanimljivo je pogledati koliko su različiti biomorfi koje je algoritam vratio kao rješenja. Na slici 10 prikazan je biomorf koji je optimalno rješenje problema (gore lijevo), kao i 5 najboljih rješenja koja nisu optimalna. Ostala rješenja poredana su po podobnosti (dolje desno je najlošije rješenje).

Slika 10: Fenotip biomorfa koje je algoritam vratio kao rješenje problema.

Kao zadnji primjer sa simetričnim biomorfima promotrimo prostor u kojem su biomorfi kažnjeni ukoliko im grane imaju vrhove u određenim dijelovima ravnine, a nagrađeni ukoliko imaju vrhove u nekim drugim dijelovima ravnine. To znači da postoji velika vjerojatnost da algoritam zapne u lokalnom optimumu (situacija u kojoj nijedan biomorf nema nijednu granu ni u području koje se nagrađuje, ni u području koje se kažnjava). Neka rješenja (gore lijevo je optimalno rješenje), kao i dijelovi za koje biomorfi dobivaju kaznu, odnosno nagradu prikazani su na slici 11.

Slika 11: Fenotip biomorfa koje je algoritam vratio kao rješenje problema. Crvena crta je granica koju biomorfi ne mogu prijeći bez kazne. Sivo osjenčano područje je područje u kojem dobivaju nagradu.

U tablici 5 dani su podaci o izvršavanju algoritma. Vidimo velik pad u kvaliteti rješenja, tj. izrazito veliko najveće i prosječno odstupanje od najboljeg rješenja. Ipak, algoritam je sa sva 4 seta podataka pronašao identično najbolje rješenje. Pregledom rješenja s jako velikim odstupanjem od najboljeg rješenja ispostavilo se da to zaista jesu biomorfi koji nisu uspjeli doći do područja s nagradom (ostali su u neosjenčanom području oko ishodišta, ali i unutar crvene linije). Ovo je dobar primjer problema u kojem bi dobra inicijalizacija mogla bitno poboljšati algoritam. Naime, ukoliko na početku u populaciju ubacimo par jedinki koje imaju neke grane u sivom području, a da ne prelaze crvenu liniju, možemo smanjiti vjerojatnost zapinjanja u lokalnom optimumu. Primijetimo pozitivan učinak koji ima povećanje broja jedinki u turniru, kao i negativan utjecaj koji ima smanjenje broja djece. Također, povećanje parametra mutacije bitno je pogoršalo prosječnu kvalitetu rješenja.

Tablica 5: Podaci o izvedbi algoritma

I za kraj, spomenimo da biomorfi mogu biti i asimetrični. Tada, umjesto 8 gena koji određuju smjer i kut među granama, koriste se 16 gena, dok sedamnaesti gen određuje broj nivoa u biomorfu. Neki primjeri asimetričnih biomorfa nalaze se na slici 12.

Slika 12: Neki asimetrični biomorfi.

5Zaključak

Kao zaključak ovih eksperimenata možemo istaknuti da izbor optimalnih parametara uvelike ovisi o tipu problema koji želimo riješiti. Dok kod najjednostavnijih problema izbor najboljih parametara i nije bio od presudne važnosti jer su se svi setovi parametara dobro nosili s problemom, kod kompleksnijih problema počele su se primijećivati neke razlike. Od bitnijih stvari možemo istaknuti negativan efekt koji relativno velik parametar mutacije ima kod traženja rješenja na prostoru s jednim globalnim optimumom mnogo boljim od lokalnih optimuma, dok kod prostora s više lokalnih optimuma bliskih po vrijednosti globalnom optimumu povećanje parametra mutacije može imati pozitivan efekt. Također, na svim primjerima potvrdilo se da povećanje broja jedinki u turniru dovodi do mnogo bržeg pronalaska rješenja, no povećava i šansu zapinjanja u lokalnom optimumu. Ipak, najnegativniji je učinak na izvedbu algoritma u svim primjerima imalo preveliko smanjivanje broja djece. Na kraju napomenimo da su ovi primjeri ilustrirali samo jedan mali dio raznolikosti biomorfa, koji su reprezentirani sa samo 9 gena.

Bibliografija

[1]

R. Dawkins, The blind watchmaker, Norton & Company, Inc, New York, NY, 1986.

[2]

A.E. Eiben i J.E. Smith, Introduction to Evolutionary Computing, Springer, 2003.

Kvantitativne metode odlučivanja - problem složene razdiobe ulaganja

optimizacija

Tihana Strmečki, Ivana Božić i Bojan Kovačić

Tehničko veleučilište u Zagrebu, Zagreb, Vrbik 8a,

U članku [1] opisan je problem jednostavne razdiobe ulaganja uz razmatranje nekoliko ilustrativnih primjera rješavanja toga problema. U njemu smo razmatrali problem razdiobe određene veličine na određene kategorije prema određenim uvjetima, pri čemu su sve kategorije bile međusobno ravnopravne, tj. niti jedna od njih nije bila preferirana u odnosu na bilo koju drugu. Stoga su komponente vrijednosti optimalnoga rješenja praktički bile zavisne samo o pripadnim koeficijentima u funkciji cilja, te o konačnim podskupovima skupa nenegativnih cijelih brojeva koji su bili definirani prema tzv. prirodnim uvjetima.

U ovom ćemo članku razmatrati odabrane primjene problema složene razdiobe ulaganja i način njihovih rješavanja primjenom metoda i tehnika dinamičkoga programiranja. Problem složene razdiobe ulaganja predstavlja svojevrsno poopćenje problema jednostavne razdiobe ulaganja. Temeljna razlika u odnosu na problem jednostavne razdiobe ulaganja jest što je svakoj pojedinoj kategoriji (npr. gospodarskoj grani, tvrtki, odjelu unutar iste tvrtke i sl.) pridružen tzv. težinski koeficijent. To konkretno znači da pri razdiobi ukupnoga novčanog iznosa na određene kategorije te kategorije nisu međusobno ravnopravne, nego rangirane prema nekom kriteriju. Pritom ne nužno postoji jedinstvena najbolje rangirana kategorija i/ili jedinstvena najslabije rangirana kategorija. Točnije, pretpostavljamo da postoje barem dvije kategorije s različitim rangovima jer se u suprotnom problem složene razdiobe ulaganja svodi na problem jednostavne razdiobe ulaganja. (Ekvivalentno, možemo reći da su u problemu jednostavne razdiobe ulaganja težinski koeficijenti unimorfno raspodijeljeni, dok su u problemu složene razdiobe ulaganja prilagođeni.)

U rješavanju problema složene razdiobe ulaganja također je pogodno primijeniti iste metode i tehnike dinamičkoga programiranja koje se primjenjuju u rješavanju problema jednostavne razdiobe ulaganja, ali uz neke neznatne preinake. Stoga su problem jednostavne razdiobe ulaganja i problem složene razdiobe ulaganja primjeri različitih klasa problema koji se rješavaju istim matematičkim metodama i tehnikama. Te se klase smatraju različitima (preciznije, neizomorfnima) zbog već spomenutog rangiranja kategorija. Slične primjere različitih klasa problema koji se rješavaju istim metodama susrećemo već i u srednjoj školi: npr. sustav jedne linearne jednadžbe s dvije nepoznanice i jedne kvadratne jednadžbe s dvije nepoznanice najprikladnije je riješiti metodom zamjene (supstitucije), a ista se metoda – kako nam je dobro poznato još iz osnovne škole – primjenjuje i npr. u rješavanju sustava dviju linearnih jednadžbi s dvije nepoznanice.

Odmah istaknimo uobičajenu „zamku" vezanu uz spomenuto rangiranje kategorija. Naime, posve se pogrešno smatra da kategorija s boljim rangom (tj. s većim težinskim koeficijentom) nužno ima i veću optimalnu vrijednost. Kako ćemo vidjeti u Primjeru 1., (naj)bolje rangirana kategorija uopće se ne mora pojaviti u optimalnom rješenju. U Primjeru 2. vidjet ćemo da se u optimalnom planu pojavljuju vrijednosti pridružene najboljoj i najslabije rangiranoj kategoriji, dok se srednje rangirana kategorija uopće ne pojavljuje u tom planu. Slobodno možemo reći da optimalna vrijednost pridružena pojedinoj kategoriji zavisi o pripadnom koeficijentu u funkciji cilja i o pripadnom težinskom koeficijentu.

Težinski koeficijenti u pravilu su unaprijed zadane strogo pozitivne realne konstante. Međutim, oni mogu biti zadani i kao funkcije. U Primjeru 3. težinski koeficijent pridružen jednoj kategoriji zadan je upravo na taj način, tj. kao tablično definirana funkcija. U Primjerima 4. i 5. vidjet ćemo kako nam težinski koeficijenti mogu bitno „smanjiti“, odnosno „povećati“ skupove nenegativnih cijelih brojeva koji su određeni tzv. prirodnim uvjetima koje moraju zadovoljavati vrijednosti pojedine varijable u matematičkom modelu. Takve „promjene“ nisu karakteristične za problem jednostavne razdiobe ulaganja, pa je to još jedna od važnih suštinskih razlika ovih dviju klasa problema.

Kad god to bude moguće, isti primjer riješit ćemo i analitički i pomoću računalnoga programa WinQSB [1]. U gotovo svim primjerima (osim Primjera 3.) provest ćemo i dodatnu što-ako analizu u kojoj ćemo – koristeći navedeni računalni program – ispitati osjetljivost optimalnoga rješenja u odnosu na promjene početnih uvjeta na pojedine komponente. Ta se analiza često rabi prigodom rješavanja problema iz gospodarske i tehničke prakse jer stjecajem različitih okolnosti može doći do naknadnih promjena početnih uvjeta.

Standardno označavamo:

[n] := {1, 2, …, n} – skup prvih n prirodnih brojeva;

[n]₀ := {0, 1, …, n} – skup prvih n + 1 elemenata skupa N₀ := {0, 1, 2, … }.

Primjer 1. [2], a montažom jednog objekta tipa B ostvaruje se dobit od 12 n.j. Pri montaži obaju tipova objekata koristi se posebna oprema čiji je ukupni raspoloživi kapacitet 10 komada. Za montažu jednoga objekta tipa A potrebna su 2 komada, a za montažu jednog objekta tipa B 3 komada te opreme. Tvrtka Muljažić – gradnja d.o.o. želi ostvariti maksimalnu dobit istodobnom montažom objekata obaju navedenih tipova, pri čemu je dopušteno da pojedini tip objekta uopće ne bude montiran i da ne bude korištena sva raspoloživa posebna oprema.

a) Odredimo matematički model promatranoga problema.

b) Nađimo optimalan plan montaže.

c) Ispitajmo kako na optimalan plan montaže utječe poseban ugovor kojim se tvrtka obvezuje da će montirati najmanje jedan, a najviše tri objekta tipa A.

Matematički model: Ovaj primjer pripada u opći problem razdiobe ulaganja jer dijelimo ukupan raspoloživi kapacitet dodatne opreme na dva dijela prema određenim kriterijima i uz ostvaraj određenoga cilja (maksimizacije ukupne dobiti). Označimo s x₁ ukupan broj objekata tipa A, a s x₂ ukupan broj objekata tipa B koje će tvrtka montirati. Ukupna dobit od montaže jednoga objekta tipa A iznosi 8 n.j., pa ukupna dobit od montaže x₁ objekata tipa A iznosi 8 × x₁ n.j. Analogno, ukupna dobit od montaže x₂ objekata tipa B iznosi 12 × x₂. Prema tome, ukupna dobit koja se dobije montažom obaju tipova objekata iznosi:

f (x₁, x₂) = 8 × x₁ + 12 × x₂.

Nadalje, ako za montažu jednog objekta tipa A tvrtka treba dva komada posebne opreme, onda za istodobnu montažu x₁ objekata tipa A tvrtka treba 2 × x₁ komada posebne opreme. Potpuno analogno, za istodobnu montažu x₂ objekata tipa B potrebno je 3 × x₂ komada posebne opreme. Budući da ukupan broj komada posebne opreme ne smije premašiti raspoloživi kapacitet, mora vrijediti nejednakost

2 × x₁+ 3 × x₂\(\leq\)10.

Prema prirodi postavljenoga problema, x₁ i x₂ moraju biti nenegativni cijeli brojevi, jer broj montiranih komada ne može biti niti decimalan broj niti negativan broj, tj.

x_i Î N₀, za i = 1, 2.

Dakle, traženi matematički model je:

maksimizirati f(x₁, x₂) = 8 × x₁ + 12 × x₂

pod uvjetima

2 × x₁+ 3 × x₂\(\leq\)10

x_i Î N₀, za i = 1, 2.

Napomena 1. U prvom od navedenih dvaju uvjeta prirodni brojevi 2 i 3 su ranije spomenuti težinski koeficijenti. Iz tog uvjeta možemo „očitati" da su objekti tipa B „vrjedniji" prema kriteriju potrebne dodatne opreme jer je za montažu jednoga od njih potrebno više dodatne opreme nego za montažu jednoga objekta tipa A. Da za jedan objekt svakoga od spomenutih dvaju tipova treba jednaka količina dodatne opreme, oba bi tipa objekata imala jednaki rang i problem bismo mogli svesti na problem jednostavne razdiobe ulaganja.

Napomena 2. Drugi uvjet možemo zamijeniti strožijim uvjetima: x₂\(\in\) [5]₀, x₂ \(\in\) [3]₀ jer je iz prirode razmatranoga problema razvidno da ukupan broj montiranih objekata tipa A ne može biti strogo veći od 5, dok ukupan broj montiranih objekata tipa B ne može biti strogo veći od 3. (Navedene rezultate formalno dobijemo rješavajući nejednadžbe \(2 \cdot x_1 \le 10 \) i \(3\cdot x_2 \le 10\) u skupu N₀.) Takvo „postroženje“ uvjeta vrlo je korisno za analitičko rješavanje zadatka, dok za rješavanje zadatka pomoću računalnoga programa WinQSB formalno nije nužno, ali je korisno radi „ubrzanja“ rada programa.

Analitičko rješenje: Stavimo S = [10]₀, pa za svaki s Î S računajmo vrijednosti funkcija

f₁(s) = \(\mathop {\max }\limits_{0 \le 2 \cdot {x_1} \le s} (8 \cdot {x_1}) = \mathop {\max }\limits_{0 \le {x_1} \le \frac{s}{2}} (8 \cdot {x_1})\)

f₂(s) = \(\mathop {\max }\limits_{0 \le 3 \cdot {x_2} \le s} \left[ {12 \cdot {x_2} + {f_1}(s - 3 \cdot {x_2})} \right] = \mathop {\max }\limits_{0 \le {x_2} \le \frac{s}{3}} \left[ {12 \cdot {x_2} + {f_1}(s - 3 \cdot {x_2})} \right]\)

Prva funkcija računa optimalnu dobit u slučaju kad se sva raspoloživa posebna oprema koristi isključivo za montiranje objekata tipa A, a druga funkcija računa optimalnu dobit kad se sva raspoloživa posebna oprema koristi za montažu obaju tipova objekata. Budući da je dozvoljeno ne iskoristiti svu raspoloživu posebnu opremu, računaju se vrijednosti obiju funkcija za svaki s \(\in\) [10]₀.

Vrijednosti navedenih funkcija računamo potpuno analogno kao i u problemima jednostavne razdiobe ulaganja (vidjeti [1], [3], [4] ili [7]). Pripadnu optimalnu vrijednost varijable x₁ označavamo uobičajeno s \(x_1^*\). Radi ilustracije postupka, navodimo izračun vrijednosti f₁(9) i f₁(10) :

f₁(9) = \(\mathop {\max }\limits_{0 \le 2 \cdot {x_1} \le 9} (8 \cdot {x_1}) = \mathop {\max }\limits_{0 \le {x_1} \le \frac{9}{2}} (8 \cdot {x_1})\) = (u segmentu [0, \(\frac{9}{2}\)] nalazi se točno pet cjelobrojnih vrijednosti: 0, 1, 2, 3 i 4) = max {8 × 0, 8 × 1, 8 × 2, 8 × 3, 8 × 4} = 32 (pripadna optimalna vrijednost varijable x₁ iznosi \(x_1^*\) = 4);

f₁(10) = \(\mathop {\max }\limits_{0 \le 2 \cdot {x_1} \le 10} (8 \cdot {x_1}) = \mathop {\max }\limits_{0 \le {x_1} \le 5} (8 \cdot {x_1})\) = max {8 × 0, 8 × 1, 8 × 2, 8 × 3, 8 × 4, 8 × 5} = 40 (pripadna optimalna vrijednost varijable x₁ iznosi \(x_1^*\) = 5).

Izračunom svih 11 vrijednosti funkcije f₁ dobivamo sljedeću tablicu:

s	1	2	3	4	5	6	7	8	9	10
f₁(s)	0	8	8	16	16	24	24	32	32	40
\(x_1^*\)	0	1	1	2	2	3	3	4	4	5

Tablica 1. Vrijednosti funkcije f₁

U sljedećem koraku za svaki s Î S računamo vrijednosti funkcije f₂(s) koristeći Tablicu 1. Pripadnu optimalnu vrijednost varijable x₂ označavamo s \(x_2^*\). Radi ilustracije postupka, navodimo izračun f₂(9) i f₂(10):

f₂(9) = \(\mathop {\max }\limits_{0 \le 3 \cdot {x_2} \le 9} \left[ {12 \cdot {x_2} + {f_1}(9 - 3 \cdot {x_2})} \right] = \mathop {\max }\limits_{0 \le {x_2} \le 3} \left[ {12 \cdot {x_2} + {f_1}(9 - 3 \cdot {x_2})} \right]\) = max {12 × 0 + f₁(9 – 3 × 0), 12 × 1 + f₁(9 – 3 × 1), 12 × 2 + f₁(9 – 3 × 2), 12 × 3 + f₁(9 – 3 × 3)} = max {0 + f₁(9), 12 + f₁(6), 24 + f₁(3), 36 + f₁(0)} = max {0 + 32, 12 + 24, 24 + 8, 36 + 0} = 36 (pripadne optimalne vrijednosti varijable x₂ su \({(x_2^*)_1} = 1\) i \({(x_2^*)_2} = 3\));

f₂(10) = \(\mathop {\max }\limits_{0 \le 3 \cdot {x_2} \le 10} \left[ {12 \cdot {x_2} + {f_1}(10 - 3 \cdot {x_2})} \right] = \mathop {\max }\limits_{0 \le {x_2} \le \frac{{10}}{3}} \left[ {12 \cdot {x_2} + {f_1}(10 - 3 \cdot {x_2})} \right]\) = (u segmentu [0, \(\frac{{10}}{3}\)] nalaze se četiri cjelobrojne vrijednosti: 0, 1, 2 i 3) = max {12 × 0 + f₁(10 – 3 × 0), 12 × 1 + f₁(10 – 3 × 1), 12 × 2 + f₁(10 – 3 × 2), 12 × 3 + f₁(10 – 3 × 3)} = max {0 + f₁(10), 12 + f₁(7), 24 + f₁(4), 36 + f₁(1)} = max {0 + 40, 12 + 16, 24 + 16, 36 + 0} = 40 (pripadne optimalne vrijednosti varijable x₂ su \({(x_2^*)_1}\)= 0 i \({(x_2^*)_2}\)= 2).

Izračunom svih 11 vrijednosti funkcije f₂ dobivamo sljedeću tablicu:

s	1	2	3	4	5	6	7	8	9	10
f₂(s)	0	8	12	16	20	24	28	32	36	40
\(x_2^*\)	0	0	1	0	1	0 ili 2	1	0 ili 2	1 ili 3	0 ili 2

Tablica 2. Vrijednosti funkcije f₂

Dakle, optimalna dobit iznosi f₂(10) = 40 n.j. i postiže se za \(x_2^*\) = 0 ili \(x_2^*\) = 2. Stoga postoje dva moguća optimalna plana montaže:

Plan 1. \(x_2^*\) = 0 znači da se ne predviđa montaža niti jednog objekta tipa B. Pripadna optimalna vrijednost funkcije f₁ je f₁(10 – 3 × 0) = f₁(10) = 40, a postiže se za \(x_1^*\) = 5. Prema tome, treba montirati točno pet objekata tipa A.

Plan 2. \(x_2^*\) = 2 znači da treba montirati dva objekta tipa B. Pripadna optimalna vrijednost funkcije f₁ je f₁(10 – 3 × 2) = f₁(4) = 16, a postiže se za \(x_1^*\) = 2. U ovom slučaju, dakle, treba montirati po dva objekta svakoga tipa.

Analiza osjetljivosti rješenja na dodatan uvjet: Činjenicu da prema posebnom ugovoru tvrtka treba montirati najmanje jedan, a najviše tri objekta tipa A, možemo zapisati u obliku nejednakosti:

\( 1 \le x_1 \le 3. \)

Možemo očekivati da ćemo kao optimalno rješenje dobiti Plan 2. jer dobiveno optimalno rješenje iz toga plana zadovoljava gornji dodatni uvjet. U ovom slučaju Tablica 1. izgleda ovako:

s	1	2	3	4	5	6	7	8	9	10
f₁(s)	0	8	8	16	16	24	24	24	24	24
\(x_1^*\)	0	1	1	2	2	3	3	3	3	3

Tablica 3. Vrijednosti funkcije f₁ uz dodatan uvjet

U odnosu na prvotno analitičko rješenje, tj. Tablicu 1., rezultati se mijenjaju jedino za s Î {8, 9, 10}, pa se dodatnim izračunom vrijednosti funkcije f₂ za te vrijednosti varijable s dobiva:

s	1	2	3	4	5	6	7	8	9	10
f₂(s)	0	8	12	16	20	24	28	32	36	40
\(x_2^*\)	0	0	1	0	1	0 ili 2	1	2	1 ili 3	2

Tablica 4. Vrijednosti funkcije f₂ uz dodatan uvjet.

Prema očekivanju, dobili smo \(x_1^*\) = \(x_2^*\) = 2, tj. Plan 2.

Rješenje pomoću programa WinQSB: Problem složene razdiobe ulaganja svodi se na ograničen cjelobrojni problem naprtnjače [3], u kojem je količina svakog predmeta ograničena nekom cjelobrojnom vrijednosti. Ukratko podsjetimo na formulaciju toga problema:

Lopov ima naprtnjaču čija je najveća dopuštena nosivost M kg. Iz trgovine može ukrasti n₁ komada namirnice N₁ čija je masa m₁, n₂ komada namirnice N₂ čija je masa m₂ itd. [4] Za svaki i \(\in\) [n] neka su x_i i v_i redom broj, odnosno vrijednost [5] ukradenih komada namirnice N_i. Kako napuniti naprtnjaču da ukupna masa svih ukradenih namirnica ne bude veća od M kg i da ukupna vrijednost svih ukradenih namirnica bude što veća? [6]

Promatrani problem naprtnjače možemo opisati sljedećim matematičkim modelom:

maksimizirati \(f({x_1},...,{x_n}) = \sum\limits_{i = 1}^n {{v_i} \cdot {x_i}} \)

pod uvjetima

\(\begin{array}{l}\sum\limits_{i = 1}^n {{m_i} \cdot {x_i}} \le M,\\{x_i} \in \left\{ {0,...,{n_i}} \right\}{\rm{, za svaki }}i \in \left[ n \right].\end{array}\)

Iz matematičkoga modela Primjera 1., te Napomena 1. i 2., slijedi da su problem iz Primjera 1. i ograničeni cjelobrojni problem naprtnjače međusobno izomorfni problemi [7]. Konkretno, u Primjeru 1. „ulogu“ namirnica N₁ i N₂ imaju objekti tipa A i B, „ulogu“ masa namirnica imaju komadi posebne opreme potrebni za montažu jednoga objekta, dok „ulogu“ vrijednosti namirnica imaju ukupne dobiti od montaže objekata. Lako se vidi da se matematički model Primjera 1. dobije tako da se u gornji model problema naprtnjače uvrsti i = 2, m₁ = 2, m₂ = 3, M = 10, v₁ = 8, v₂ = 12, n₁ = 5 i n₂ = 3.

Pokrenimo potprogram DP programa WinQSB. Lijevom tipkom miša kliknimo na izbornik File i odaberimo opciju New Problem. U dobivenom dijaloškom okviru lijevom tipkom miša kliknimo na kružić pored natpisa Knapsack Problem, pa u pravokutnik pored natpisa Problem Title upišimo Primjer 1, a u pravokutnik pored natpisa Number of Items upišimo 2 (jer imamo dva tipa objekata). Dobivamo Sliku 1.

Slika 1. Unos naziva i broja objekata u Primjeru 1.

Lijevom tipkom miša kliknimo na OK. U sljedećem koraku unosimo ulazne podatke:

– u drugi stupac (Item Identification) upisujemo nazive tipova objekata: A i B;

– u treći stupac (Units Available) trebali bismo upisati koliko nam je maksimalno objekata kojega tipa na raspolaganju, ali te brojeve ne znamo. Sukladno Napomeni 2, riješimo nejednadžbe \(2\cdot x_1 \le 10\) i \(3\cdot x_2 \le 10\) u skupu N₀, pa dobivamo \(x_1\le 5\) i \(x_2\le 3\). To znači da ne možemo montirati više od 5 objekata tipa A i više od 3 objekta tipa B, pa u ovaj stupac upisujemo 5 i 3.

– u četvrti stupac (Unit Capacity Required) upisujemo težinske koeficijente koji množe veličine x₁ i x₂ u uvjetu iz matematičkoga modela. To su brojevi 2 i 3, pa u četvrti stupac upisujemo redom 2 i 3.

– u peti stupac (Return Function (X: Item ID)) upisujemo komponente funkcije cilja koje odgovaraju svakom pojedinom objektu, a to je zapravo dobit od montaže svakoga pojedinog objekta. Dakle, upisujemo redom: 8*X i 12*X.

– u posljednji redak (Capacity=) upisujemo kapacitet raspoložive opreme, tj. 10.

Ovime je unos ulaznih podataka završen. Dobivamo Sliku 2.

Slika 2. Unos ulaznih podataka u Primjeru 1.

Lijevom tipkom miša kliknimo na izbornik Solve and Analyze, pa odaberimo opciju Solve the Problem. Dobivamo Sliku 3.

Slika 3. Izlazni podatci u Primjeru 1.

Iz trećega stupca dobivene tablice (Decision Quantity (X)) očitavamo optimalan plan montaže: treba montirati po dva objekta svakoga tipa. Dakle, riječ je o Planu 2. dobivenom u analitičkom rješenju.

Napomena 3. Plan 1. dobiven analitičkim rješenjem nije moguće dobiti pomoću potprograma DP. Naime, iako taj potprogram dopušta mogućnost tzv. što–ako analize (engl.: What-If Analysis) u kojoj se unaprijed može zadati optimalna vrijednost jedne od varijabli, nije dopušten unos nule kao optimalne vrijednosti bilo koje varijable, pa nije moguće dobiti Plan 1.

Primjer 2. Tvrtka Muljarević–gradnja d.o.o. istodobno treba montirati tri tipa objekata: A₁, A₂ i A₃. Pri montaži svih tipova objekata koristi se posebna oprema čiji je ukupni kapacitet 18 komada. Osnovni podaci o broju potrebnih komada posebne opreme i dobiti za izradu svakoga pojedinog tipa opreme navedeni su u Tablici 5.

tip objekta	broj potrebnih komada opreme	neto–dobit [n.j./objekt]
A₁	4	8
A₂	6	12
A₃	3	10

Tablica 5. Ulazni podatci za Primjer 2.

Odlukom uprave tvrtke dopuštena je istodobna montaža najviše tri objekta tipa A₁ i pet objekata tipa A₃. Dopušteno je da pojedini tip objekta ne bude montiran, te da ne bude iskorištena sva posebna oprema. Treba napraviti optimalan plan montaže tako da ukupna ostvarena neto–dobit bude maksimalna.

a) Odredimo matematički model promatranoga problema.

b) Nađimo optimalan plan montaže.

Matematički model: Za svaki i \(\in\) [3] neka je x_i broj objekata tipa A_i koji će biti montirani. Tada ukupna dobit od montaže objekata tipa A₁ iznosi 8 × x₁ n.j., ukupna dobit od montaže objekata tipa A₂ 12 × x₂ n.j., a ukupna dobit od montaže objekata tipa A₃ 10 × x₃ n.j. Stoga ukupna dobit od montaže svih triju tipova objekata iznosi:

f(x₁, x₂, x₃) = 8 × x₁ + 12 × x₂ + 10 × x₃.

Za montažu x₁ objekata tipa A₁ potrebno je ukupno 4 × x₁ komada posebne opreme, za montažu x₂ objekata tipa A₂ potrebno je ukupno 6 × x₂ komada posebne opreme, a za montažu x₃ objekata tipa A₃ potrebno je ukupno 3 × x₃ komada posebne opreme. Budući da ukupan broj potrebnih komada posebne opreme ne može premašiti ukupan kapacitet posebne opreme, mora vrijediti nejednakost:

\(4\cdot x_1 + 6 \cdot x_2 + 3\cdot x_3 \le 18\).

Nadalje, budući da je istodobno moguće montirati najviše tri objekta tipa A₁ i najviše pet objekata tipa A₃, moraju vrijediti nejednakosti:

x₁ \(\in\) [3]₀, x₃\(\in\) [5]₀.

Primijetimo da zbog cjelobrojnosti i nenegativnosti vrijednosti varijable x₂ iz nejednakosti 4 × x₁ + 6 × x₂ + 3 × x₃ \leq18 slijedi x₂\in [3]₀. Prema tome, traženi matematički model je:

maksimizirati f(x₁, x₂, x₃) = 8 × x₁ + 12 × x₂ + 10 × x₃

pod uvjetima

\(4\cdot x_1 + 6 \cdot x_2 + 3\cdot x_3\le 18\)

x₁, x₂ Î [3]₀,

x₃ Î [5]₀.

Analitičko rješenje: Stavimo S = [18]₀, pa za svaki s Î S računajmo vrijednosti sljedećih funkcija:

f₁(s) = \(\mathop {\max }\limits_{\scriptstyle0 \le 4 \cdot {x_1} \le s\atop\scriptstyle0 \le {x_1} \le 3} (8 \cdot {x_1}) = \mathop {\max }\limits_{0 \le {x_1} \le \min \left\{ {\frac{s}{4},{\rm{ }}3} \right\}} (8 \cdot {x_1})\)

f₂(s) = \(\mathop {\max }\limits_{\scriptstyle0 \le 6 \cdot {x_2} \le s\atop\scriptstyle0 \le {x_2} \le 3} \left[ {12 \cdot {x_2} + {f_1}(s - 6 \cdot {x_2})} \right] = \mathop {\max }\limits_{0 \le {x_2} \le \min \left\{ {\frac{s}{6},{\rm{ }}3} \right\}} \left[ {12 \cdot {x_2} + {f_1}(s - 6 \cdot {x_2})} \right]\)

f₃(s) = \(\mathop {\max }\limits_{\scriptstyle0 \le 3 \cdot {x_3} \le s\atop\scriptstyle0 \le {x_3} \le 5} \left[ {10 \cdot {x_3} + {f_2}(s - 3 \cdot {x_3})} \right] = \mathop {\max }\limits_{0 \le {x_3} \le \min \left\{ {\frac{s}{3},{\rm{ }}5} \right\}} \left[ {10 \cdot {x_3} + {f_2}(s - 3 \cdot {x_2})} \right]\)

Funkcija f₁ računa optimalnu neto–dobit ako se s komada posebne opreme koristi isključivo za montažu objekata tipa A₁. Funkcija f₂ računa optimalnu neto–dobit ako se s komada posebne opreme koristi isključivo za montažu objekata tipa A₁ i A₂. Funkcija f₃ računa optimalnu neto–dobit ukoliko se s komada opreme koristi za montažu svih triju tipova objekata.

U prvom koraku dobivamo Tablicu 6.

s	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
f₁(s)	0	0	0	8	8	8	8	16	16	16	16	24	24	24	24	24	24	24
\(x_1^*\)	0	0	0	1	1	1	1	2	2	2	2	3	3	3	3	3	3	3

Tablica 6. Vrijednosti funkcije f₁ u Primjeru 2.

u drugom koraku Tablicu 7.

s	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
f₂(s)	0	0	0	8	8	12	12	16	16	20	20	24	24	28	28	32	32	36
\(x_2^*\)	0	0	0	0	0	1	1	0	0	1	1	0, 2	0, 2	1	1	2	2	1, 3

Tablica 7. Vrijednosti funkcije f₂ u Primjeru 2.

a u trećem koraku Tablicu 8.

s	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
f₃(s)	0	0	10	10	10	20	20	20	30	30	30	40	40	40	50	50	50	52
\(x_3^*\)	0	0	1	1	1	2	2	2	3	3	3	4	4	4	5	5	5	4

Tablica 8. Vrijednosti funkcije f₃ u Primjeru 2.

Prema tome, optimalna dobit je f₃(18) = 52 n.j. i postiže se za \(x_3^*\) = 4, što znači da treba montirati ukupno četiri objekta tipa A₃. Pripadna optimalna vrijednost funkcije f₂ je f₂(18 – 3 × 4) = f₂(6) = 12 koja se postiže za \(x_2^*\) = 1, pa treba montirati jedan objekt tipa A₂. Napokon, pripadna optimalna vrijednost funkcije f₁ je f₁(6 – 6 × 1) = f₁(0) = 0 i postiže se za \(x_1^* = 0\), pa ne treba montirati niti jedan objekt tipa A₁. Dakle, optimalan plan montaže je montirati jedan objekt tipa A₂ i četiri objekta tipa A₃ uz maksimalnu neto–dobit 52 n.j.

Rješenje pomoću programa WinQSB: Navodimo samo ulazne parametre prema kojima se rješenje ovoga problema razlikuje od rješenja Primjera 1.:

– Problem Title: Primjer 2

– Number of Items: 3

– Item Identification: A1, A2, A3

– Units Available: 3, 3, 5 (jer se mogu montirati najviše tri objekta tipa A₁, odnosno tipa A₂ i najviše pet objekata tipa A₃)

– Unit Capacity Required: 4, 6, 3

– Return Function (X: Item ID): 8*X, 12*X, 10*X

– Capacity = 18

Rješavanjem problema u drugom stupcu (Decision Quantity) dobivamo vrijednosti 0, 1 i 4, pa „očitavamo'' da treba montirati točno jedan objekt tipa A₂ i četiri objekta tipa A₃. Ukupna optimalna dobit od montaže svih triju objekata (Total Return Value) iznosi 52 n.j.

Napomena 5: U ovome je slučaju zgodno provesti što – ako analizu, pa npr. istražiti kako će se promijeniti optimalni plan odlučimo li montirati točno jedan objekt tipa A₁. U tu svrhu iskoristimo rezultat dobiven programom WinQSB. Kliknemo lijevom tipkom miša na ikonicu What If, pa u presjeku retka A1 i stupca Preset Decision upišimo 1. Ovim smo zapravo unaprijed definirali odluku da želimo montirati točno jedan objekt tipa A₁.[8] Iz tablice na desnoj strani toga okvira „očitamo'' da, uz navedeni dodatni uvjet, treba montirati jedan objekt tipa A₁ i četiri objekta tipa A₃. Dakle, postavljanje dodatnoga uvjeta izazvalo je smanjenje optimalne vrijednosti varijable x₂, a nije utjecalo na optimalnu vrijednost varijable x₃.

Primjer 3. Brodom treba prevesti dvije vrste robe: A i B. Dobit po jednom komadu robe A iznosi 40 n.j., a dobit po jednom komadu robe B 60 n.j. Jedan komad robe B zauzima pet kub. jed.brodskoga prostora [9]. Roba A zauzima brodski prostor u zavisnosti o količini utovarene robe prema Tablici 9.:

količina robe A

[kom.]

potreban obujam brodskoga prostora

[kub. jed.]

Tablica 9. Zavisnost obujma brodskoga prostora o količini utovarene robe A

Obujam dijela broda namijenjenog za prijevoz robe iznosi 20 kub. jed. Komadi obiju vrsta robe su nedjeljivi. Moguće je ne prevesti niti jedan komad pojedine vrste robe, te ne iskoristiti sav obujam dijela broda namijenjenog za prijevoz robe. Treba napraviti optimalan plan utovara robe A i B tako da se ostvari maksimalna dobit.

a) Odredimo matematički model promatranoga problema.

b) Nađimo optimalan plan utovara broda i iznos maksimalne dobiti.

Matematički model: Neka je x_A količina utovarene robe vrste A, a x_B količina utovarene robe vrste B. Tada ukupna dobit ostvarena prijevozom robe vrste A iznosi 40 × x_A n.j., a ukupna dobit ostvarena prijevozom robe vrste B iznosi 60 × x_B n.j. Prema tome, ukupna dobit ostvarena prijevozom obiju vrsta roba iznosi

f(x_A, x_B) = 40 × x_A + 60 × x_B.

Označimo s O_A(x) funkciju koja količini robe A pridružuje potreban obujam brodskoga prostora. Funkcija O_A(x) je definirana tablično (Tablicom 9.) i najveća vrijednost njezina argumenta iznosi 6. To znači da se brodom može prevesti najviše šest komada robe A, pa zbog prirodne cjelobrojnosti vrijednosti x_A vrijedi uvjet:

x_A Î [6]₀.

S druge strane, vrijednost varijable B je također nenegativna i cjelobrojna. Da bismo izbjegli postavljanje „slaboga“ uvjeta x_B Î N₀, uočimo da iz podatka da jedan komad robe B zauzima pet kub.jed. i iz podatka da obujam dijela broda namijenjenoga za prijevoz robe iznosi 20 kub. jed. slijedi da na brod ne možemo utovariti strogo više od četiri komada robe B, tj. uvjet na vrijednost varijable x_B možemo postrožiti na sljedeći uvjet:

x_B Î [4]₀.

Preostaje još uvjetom iskazati podatak da ukupan obujam utovarene robe ne može biti strogo veći od obujma dijela broda namijenjenog za prijevoz robe. Ukupan obujam x_A komada robe A iznosi O_A(x_A), a ukupan obujam x_B komada robe B iznosi 5 × x_B, pa mora vrijediti nejednakost:

\(O_A(x_A) + 5\cdot x_B \le 20\).

Dakle, traženi matematički model promatranoga problema je:

maksimizirati f(x_A, x_B) = 40 × x_A + 60 × x_B

pod uvjetima

\(O_A(x_A) + 5\cdot x_B \le 20\).

x_A Î [6]₀,

x_B Î [4]₀.

Rješenje: Odmah napomenimo da, zbog tabličnoga definiranja funkcije ovisnosti obujma brodskoga prostora o količini robe A, ovaj problem nije moguće riješiti primjenom programa WinQSB jer taj program zahtijeva definiranje navedene funkcije analitičkim izrazom (formulom). Stavimo S = [20]₀, pa za svaki s Î S računajmo vrijednosti funkcija:

f₁(s) = \(\mathop {\max }\limits_{0 \le {O_A}({x_A}) \le s} (40 \cdot {x_A})\)

f₂(s) = \(\mathop {\max }\limits_{\scriptstyle0 \le 5 \cdot {x_B} \le s\atop\scriptstyle0 \le {x_B} \le 4} \left[ {60 \cdot {x_B} + {f_1}(s - 5 \cdot {x_B})} \right] = \mathop {\max }\limits_{0 \le {x_B} \le \min \left\{ {\frac{s}{5},{\rm{ }}4} \right\}} \left[ {60 \cdot {x_B} + {f_1}(s - 5 \cdot {x_B})} \right]\)

Funkcija f₁(s) računa optimalnu dobit ako se svih s kub. jed. prostora namijenjenog za prijevoz robe iskoristi isključivo za prijevoz robe vrste A, dok funkcija f₂(s) računa optimalnu dobit ako se taj prostor iskoristi za prijevoz obiju vrsta roba.

Radi ilustracije postupka, prikazujemo izračun vrijednosti funkcija f₁ i f₂ za s = 17 i s = 20:

f₁(17) = \(\mathop {\max }\limits_{0 \le {O_A}({x_A}) \le 17} (40 \cdot {x_A})\) = max {40 × 0, 40 × 1, 40 × 2, 40 × 3, 40 × 4, 40 × 5} = 200;

f₂(17) = \(\mathop {\max }\limits_{0 \le {x_B} \le \frac{{17}}{5}} \left[ {60 \cdot {x_B} + {f_1}(17 - 5 \cdot {x_B})} \right]\) = max{60 × 0 + f₁(17), 60 × 1 + f₁(12), 60 × 2 + f₂(7), 60 × 3 + f₂(2)} = max{0 + 200, 60 + 160, 120 + 40, 180 + 0} = 220;

f₁(20) = \(\mathop {\max }\limits_{0 \le {O_A}({x_A}) \le 18} (40 \cdot {x_A})\) = max {40 × 0, 40 × 1, 40 × 2, 40 × 3, 40 × 4, 40 × 5, 40 × 6} = 240;

f₂(20) = \(\mathop {\max }\limits_{0 \le {x_B} \le 4} \left[ {60 \cdot {x_B} + {f_1}(20 - 5 \cdot {x_B})} \right]\) = max{60 × 0 + f₁(20), 60 × 1 + f₁(15), 60 × 2 + f₂(10), 60 × 3 + f₂(5), 60 × 4 + f₂(0)} = max{0 + 240, 60 + 200, 120 + 120, 180 + 40, 240 + 0} = 260.

Izračunom svih vrijednosti funkcija f₁ i f₂ dobiva se Tablica 10.:

s	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
f₁(s)	0	0	0	0	40	40	40	80	80	120	120	160	160	160	200	200	200
\(x_A^*\)	0	0	0	0	1	1	1	2	2	3	3	4	4	4	5	5	5
f₂(s)	0	0	0	0	60	60	60	80	80	120	120	160	160	160	200	200	220
\(x_B^*\)	0	0	0	0	1	1	1	0	0	0, 2	0, 2	0	0	0	0	0	1

s	18	19	20
f₁(s)	240	240	240
\(x_A^*\)	6	6	6
f₂(s)	240	240	260
\(x_B^*\)	0	0	1

Tablica 10. Vrijednosti funkcija f₁ i f₂.

Prema tome, optimalna dobit je f₂(20) = 260 i postiže se za \(x_B^*\) = 1. Odgovarajuća optimalna vrijednost funkcije f₁ je f₁(20 – 5 × 1) = f₁(15) = 200 i postiže se za \(x_A^*\) = 5. Dakle, optimalan plan prijevoza robe je prevesti pet komada robe vrste A i jedan komad robe vrste B.

Primjer 4. Zrakoplovom nosivosti 83 tone treba prevesti tri vrste robe čije su jedinične mase i jedinične dobiti od prijevoza naveden u sljedećoj tablici.

vrsta robe	A	B	C
jedinična masa [t]	24	22	16
jedinična dobit [n.j.]	96	85	50

Tablica 11. Ulazni podatci za Primjer 4.

Komadi svih triju vrsta robe su nedjeljivi. Treba napraviti plan utovara svih triju vrsta robe tako da se ostvari maksimalna dobit.

a) Odredimo matematički model promatranoga problema.

b) Nađimo optimalan plan utovara i odgovarajuću maksimalnu dobit.

Matematički model: Neka su x_A količina utovarene robe vrste A, x_B količina utovarene robe vrste B i x_C količina utovarene robe vrste C. Tada ukupna dobit od prijevoza robe vrste A iznosi 96 × x_A, ukupna dobit od prijevoza robe vrste B iznosi 85 × x_B, a ukupna dobit od prijevoza robe vrste C iznosi 50 × x_C. Stoga je ukupna dobit od prijevoza svih triju vrsta roba

f(x_A, x_B, x_C) = 96 × x_A + 85 × x_B + 50 × x_C.

Nadalje, ukupna masa x_A komada robe vrste A iznosi 24 × x_A tona, ukupna masa x_B komada robe vrste B iznosi 22 × x_B tona, a ukupna masa x_C komada robe vrste C iznosi 16 × x_C tona. Ukupna masa svih triju vrsta robe ne smije biti strogo veća od nosivosti zrakoplova, što znači da mora vrijediti uvjet:

24 × x_A + 22 × x_B + 16 × x_C \(\le\) 83.

Prema prirodi problema, sve tri vrijednosti x_A, x_B i x_C su nenegativni cijeli brojevi. Kao i u prethodnim primjerima, međutim, možemo postupiti „lukavije“, pa uočiti da iz nejednakosti

\(24\cdot x_A \le 83\),

\(22\cdot x_B \le 83\),

\(16\cdot x_C \le 83\),

slijedi

x_A, x_B \(\in\) [3]₀,

x_C \(\in\) [5]₀,

Dakle, traženi matematički model promatranoga problema je:

maksimizirati f(x_A, x_B, x_C) = 96 × x_A + 85 × x_B + 50 × x_C

pod uvjetima

24 × x_A + 22 × x_B + 16 × x_C \(\le\) 83

x_A, x_B \(\in\) [3]₀,

x_C \(\in\) [5]₀,

Analitičko rješenje: Prepuštamo ga čitatelju.

Rješenje pomoću računalnoga programa WinQSB: Navodimo samo parametre prema kojima se rješenje ovoga primjera razlikuje od prethodno navedenih rješenja:

– Problem Title: Primjer 4

– Number of Items: 3

– Item Identification: A, B, C

– Units Available: 3, 3, 5.

– Unit Capacity Required: 24, 22, 16

– Return Function (X: Item ID): 96*X, 85*X, 50*X

– Capacity = 83

Nakon pokretanja procedure Solve and Analyze u stupcu Decision Quantity „očitavamo'' vrijednosti 0, 3 i 1. Dakle, optimalan plan utovara je: utovariti tri komada robe B i jedan komad robe C. Ukupna optimalna dobit (Total Return Value) iznosi 305 n.j.

I ovdje možemo provesti što–ako analizu, pa promotriti kako na dobiveno optimalno rješenje utječe npr. dodatni uvjet da se mora prevesti točno jedan komad robe A. U tom je slučaju optimalni plan utovara: utovariti po jedan komad robe svake od vrsta A i B, te točno 2 komada robe vrste C. Dakle, postavljanje dodatnoga uvjeta uzrokuje promjenu obiju optimalnih vrijednosti: optimalna vrijednost x_B se smanjila, dok se optimalna vrijednost x_C povećala.

Primjer 5. Zrakoplovom nosivosti 50 tona na određenoj se liniji mogu prevoziti putnici, poštanske pošiljke i ostali teret. Prosječna masa i dobit ostvarena po jedinici transporta navedeni su u donjoj tablici.

	1 putnik	1 poštanski paket	1 paket ostalog tereta
prosječna masa [t]	0.085	0.2	0.9
dobit [000 n.j.]	2	2.5	4.5

Tablica 12. Ulazni podatci za Primjer 5.

U zrakoplov se može smjestiti najviše 120 putnika. Treba odrediti optimalnu strukturu transporta tako da se ostvari maksimalna dobit. Formirajmo odgovarajući matematički model, pa odredimo traženu optimalnu strukturu.

Matematički model: Neka su x₁ broj putnika, x₂ broj poštanskih paketa i x₃ broj paketa drugoga tereta koji će se prevoziti zrakoplovom. Ukupna dobit ostvarena prijevozom x₁ putnika iznosi 2 × x₁ [000 n.j.], ukupna dobit ostvarena prijevozom x₂ poštanskih paketa iznosi 2.5 × x₂ [000 n.j.], a ukupna dobit ostvarena prijevozom x₃ paketa ostaloga tereta je 4.5 × x₃ [000 n.j.]. Stoga ukupna dobit nastala prijevozom svih triju kategorija tereta iznosi:

f (x₁, x₂, x₃) = 2 × x₁ + 2.5 × x₂ + 4.5 × x₃.

Nadalje, ukupna masa svih x₁ putnika iznosi 0.085 × x₁ tona, ukupna masa x₂ poštanskih paketa iznosi 0.2 × x₂ tona, a ukupna masa x₃ paketa ostaloga tereta je 0.9 × x₃ tona. Budući da ukupna masa svih triju vrsta tereta ne smije biti strogo veća od nosivosti zrakoplova, mora vrijediti nejednakost:

0.085 × x₁ + 0.2 × x₂ + 0.9 × x₃ \(\le\) 50.

Analogno kao u prethodnim primjerima, iz navedene nejednakosti slijedi:

x₁ \(\in\) [588]₀,

x₂\(\in\) [250]₀,

x₃ \(\in\) [56]₀.

Međutim, zbog podatka da se u zrakoplov može smjestiti najviše 120 putnika, prvi uvjet moramo preinačiti u:

x₁ \(\in\) [120]₀,.

Tako matematički model promatranoga problema glasi:

maksimizirati f (x₁, x₂, x₃) = 2 × x₁ + 2.5 × x₂ + 4.5 × x₃

pod uvjetima

0.085 × x₁ + 0.2 × x₂ + 0.9 × x₃ \(\le\) 50

x₁ \(\in\) [120]₀,

x₂ \(\in\) [250]₀,

x₃ \(\in\) [56]₀.

Analitičko rješenje: Zbog opsežnosti ga izostavljamo.

Rješenje pomoću programa WinQSB: Navodimo samo parametre prema kojima se rješenje ovoga primjera razlikuje od ranije navedenih rješenja:

– Problem Title: Primjer 5

– Number of Items: 3

– Item Identification: putnici, poštanski paket, ostali teret

– Units Available: opet postupimo lukavo, pa u skupu N riješimo nejednadžbe 0.2 × x₂\(\le\) 50 i 0.9 × x₃ \(\le\) 50 i dobivamo: x₂\(\le\)250, x₃ \(\le\) 55. Stoga u ovaj stupac upisujemo: 120, 250, 55.

– Unit Capacity Required: 0.085, 0.2, 0.9

– Return Function (X: Item ID): 2*X, 2.5*X, 4.5*X

– Capacity = 50

Nakon pokretanja procedure Solve and Analyze u stupcu Decision Quantity „očitavamo'' vrijednosti 120, 199 i 0. Dakle, optimalnu strukturu transporta tvori 120 putnika i 199 poštanskih paketa uz ukupnu optimalnu dobit (Total Return Value) 737.50 [000 n.j.], odnosno 737 500 n.j.

Postavimo li npr. dodatni uvjet da moramo prevesti i točno jedan paket ostaloga tereta, što–ako analizom dobivamo sljedeću optimalnu strukturu transporta: 120 putnika, 194 poštanska paketa i 1 paket ostaloga tereta. Dakle, postavljanje dodatnog uvjeta nije utjecalo na optimalan broj putnika u optimalnoj strukturi transporta, ali je smanjilo optimalan broj poštanskih paketa u optimalnoj strukturi transporta.

Zaključak

Ovim primjerom završavamo razmatranje problema složene razdiobe ulaganja. Primijetimo da smo u rješavanju gotovo svakoga primjera zapravo preinačili originalni matematički model (koji je proizašao iz formulacije problema), a s ciljem što jednostavnijega i bržega iznalaženja optimalnoga rješenja. Takve preinake u rješavanju problema jednostavne razdiobe ulaganja u pravilu nisu moguće, odnosno praktički se pojavljuju jedino u naknadnim što-ako analizama. Također, u Primjerima 1. i 2. iz članka [1] mogli smo unaprijed naslutiti optimalno rješenje (koristeći npr. pohlepni algoritam). No, pri rješavanju problema složene razdiobe ulaganja optimalno rješenje u pravilu ne možemo unaprijed naslutiti, pa treba izbjegavati procjenjivanje vrijednosti njegovih komponenti (čemu su rješavači problema nerijetko vrlo skloni).

Zbog mogućnosti pojave najmanje dvaju optimalnih planova (vidjeti Primjer 1.), od kojih računalnim programom možemo dobiti točno jedno, u praksi treba nastojati što je više moguće kombinirati oba izložena načina rješavanja. Rješavanje samo pomoću računalnoga programa treba primijeniti ponajviše u slučajevima poput Primjera 5. kad je provedba analitičkoga načina rješavanja tehnički relativno složena i spora.

LITERATURA:

[1.] T. Strmečki i B. Kovačić: Kvantitativne metode odlučivanja – problem jednostavne razdiobe ulaganja, Math.e Vol. 19, Zagreb, 2011.

[2.] M.J. Beckmann: Dynamic Programming of Economic Decisions, Springer–Verlag, New York, 1968.

[3.] R.Bellman: Dynamic Programming, Dover Publications, 2003.

[4.] D. Kalpić, V. Mornar: Operacijska istraživanja, ZEUS, Zagreb, 1996.

[5.] L. Neralić: Uvod u matematičko programiranje 1, Element, Zagreb, 2003.

[6.] J. Petrić: Operaciona istraživanja, Nauka, Beograd, 1997.

[7.] J. Petrić et.al.: Operaciona istraživanja – zbirka rešenih zadataka, Nauka, Beograd, 1996.

[8.] H. Kellerer,U. Pferschy,D. Pisinger: Knapsack problems, Springer, 2004.

[9.] S. Martello, P. Toth: Knapsack problems, Wiley, 1990.

DODATAK

U Dodatku navodimo još nekoliko primjera iz klase problema složene razdiobe ulaganja, a u čijem se rješavanju primjenjuju metode i tehnike dinamičkoga programiranja. Ti se primjeri rješavaju na potpuno analogan način kao i Primjeri 1. – 5., pa njihovo rješavanje prepuštamo čitatelju. U svakom pojedinom primjeru osobitu pozornost treba posvetiti formiranju matematičkoga modela razmatranoga problema jer je to najvažnija (i najteža) faza u procesu rješavanja zadatka. Kad god je to moguće, preporučujemo riješiti primjer i analitički i pomoću računalnoga programa WinQSB.

Zadatak 1. Brodski teret tvore četiri različita artikla. Jedinična masa i jedinična dobit za svaki pojedini artikl navedeni su u sljedećoj tablici.

artikl	jedinična masa [tona]	jedinična dobit [n.j.]
A	2	50
B	4	120
C	5	170
D	3	80

Ukupna masa brodskoga tereta može biti najviše 9 tona. Niti jedan komad svake vrste robe

nije moguće podijeliti na manje dijelove. Treba naći optimalan plan utovara kojim se postiže maksimalna dobit.

a) Formirajte matematički model promatranoga problema.

b) Nađite optimalan plan utovara i odgovarajuću maksimalnu dobit.

c) Ako je optimalna količina nekog artikla jednaka nuli, istražite kako njeno povećanje za 1 komad utječe na optimalne količine ostalih artikala.

Rezultati: Neka su x_A, x_B, x_C i x_D redom količine artikala A, B, C i D.

a) Matematički model glasi:

maksimizirati \(z=50\cdot x_A + 120\cdot x_B +170\cdot x_C + 80\cdot x_D\)

pod uvjetima

\(2\cdot x_A+4\cdot x_B+ 5\cdot x_C+3\cdot x_D \le 9\),

x_A, x_B, x_C, x_D \(\in\) N₀.

b) \(\left( {x_A^*,x_B^*,x_C^*,x_D^*} \right) = (0,1,1,0)\), tj. optimalan plan je utovariti po točno jedan komad svakoga od artikala B i C. Pripadna optimalna dobit iznosi z* = 290 n.j.

c) Za \(x_A^* = 1\)ili \(x_D^* = 1\) dobivamo \(\left( {x_A^*,x_B^*,x_C^*,x_D^*} \right) = (1,1,0,1)\), pa zaključujemo da ispunjenjem dodatnog zahtjeva optimalna količina artikla B ostaje nepromijenjena, dok se optimalna količina artikla C smanji za jedan komad.

Zadatak 2. Brodom se prevoze dvije vrste robe: A i B. Po komadu prevezene robe A ostvaruje se dobit od 40 n.j., a po komadu prevezene robe B dobit od 60 n.j. Nadalje, 1 komad robe A ima obujam 3 kub. jed., a 1 komad robe B obujam 5 kub. jed. Obujam brodskoga prostora previđenoga za prijevoz obiju vrsta robe iznosi 30 kub. jed. Niti jedan komad svake vrste robe nije moguće podijeliti na manje dijelove. Treba naći optimalan plan utovara broda navedenim vrstama robe tako da dobit ostvarena od prijevoza obiju vrsta roba bude maksimalna.

a) Formirajte matematički model promatranoga problema.

b) Nađite optimalan plan utovara i odgovarajuću maksimalnu dobit.

c) Riješite b) podzadatak uz uvjet da se brodom može prevesti najviše 6 komada robe A.

Rezultati: Neka su x_A i x_B redom količine robe A i B.

a) Matematički model glasi:

maksimizirati \(z= 40\cdot x_A+60\cdot x_B\)

pod uvjetima

\(3 \cdot x_A + 5\cdot x_B \le 30\),

x_A, x_B \(\in\) N₀.

b) \(\left( {x_A^*,x_B^*} \right) = (10,0)\), tj. optimalan plan je prevesti točno 10 komada robe A. Pripadna optimalna dobit iznosi z* = 400 n.j.

c) \(\left( {x_A^*,x_B^*} \right) = (5,3)\), tj. novi optimalan plan je prevesti točno 5 komada robe A i točno 3 komada robe B. Pripadna optimalna dobit iznosi z* = 380 n.j.

Zadatak 3. Zrakoplovom nosivosti 85 tona treba prevesti tri vrste robe čije su jedinične mase i jedinične dobiti navedene u sljedećoj tablici:

vrsta robe

jedinična masa

[tona]

jedinična dobit

[000 €]

Komade svih triju vrsta robe nije moguće razdijeliti na manje dijelove. Treba napraviti optimalan plan utovara robe tako da ukupna dobit bude maksimalna.

a) Formirajte matematički model promatranoga problema.

b) Nađite optimalan plan utovara i odgovarajuću maksimalnu dobit.

c) Nađite optimalan plan utovara uz dodatni uvjet da se mora prevesti najmanje jedan komad svake vrste robe.

Rezultati: Neka su x_A, x_B i x_C redom količine robe A, B i C.

a) Matematički model glasi:

maksimizirati \(z=64\cdot x_A+ 56\cdot x_B+ 60 \cdot x_C\)

pod uvjetima

\(14 \cdot x_A + 12 \cdot x_B + 13 \cdot x_C \le 85\),

x_A, x_B, x_C \(\in\) N₀.

b) \(\left( {x_A^*,x_B^*,x_C^*} \right) = (0,6,1)\), tj. optimalan plan je prevesti točno 6 komada robe B i točno jedan komad robe C. Pripadna optimalna dobit iznosi z* = 396 000 €.

c) \(\left( {x_A^*,x_B^*,x_C^*} \right) = (1,1,4)\), tj. optimalan plan je: prevesti po točno jedan komad svake od roba A i B, te točno 4 komada robe C. Pripadna optimalna dobit iznosi z* = 360 000 €.

Zadatak 4. Tvrtka Smotalić–gradnja d.o.o. izvodi montažu dvaju tipova objekata: A i B. Montažom jednoga objekta tipa A ostvaruje se dobit od 10 n.j., a montažom jednoga objekta tipa B dobit od 12 n.j. Pri istodobnoj montaži obaju tipova objekata može se koristiti najviše 20 komada posebne vrste opreme, pri čemu za montažu jednoga objekta tipa A trebaju 4 komada opreme, a za montažu jednog objekta tipa B 3 komada opreme. Tvrtka želi istodobnim montiranjem objekata A i B ostvariti maksimalnu dobit.

a) Formirajte matematički model promatranoga problema.

b) Nađite optimalan plan montaže i odgovarajuću optimalnu dobit.

c) Ispitajte kako na optimalan plan montaže utječe poseban ugovor kojim se tvrtka obvezuje montirati barem 2, a najviše 5 objekata tipa A.

Rezultati: Neka su x_A i x_B redom brojevi („količine“) montiranih objekata tipa A i tipa B.

a) Matematički model glasi:

maksimizirati \(z= 10\cdot x_A +12 \cdot x_B\)

pod uvjetima

\(4\cdot x_A + 3\cdot x_B \le 20\),

x_A, x_B \(\in\) N₀.

b) \(\left( {x_A^*,x_B^*} \right) = (0,6)\), tj. optimalan plan je montirati samo točno 6 objekata tipa B. Pripadna optimalna dobit iznosi z* = 72 n.j.

c) \(\left( {x_A^*,x_B^*} \right) = (2,4)\), tj. optimalan plan je montirati točno 2 objekta tipa A i 4 objekta tipa B. Pripadna optimalna dobit iznosi z* = 68 n.j.

Zadatak 5. Tvrtka Gulikožić–gradnja d.o.o. raspolaže s kamionom nosivosti 45 jed. Tim kamionom treba prevesti dvije vrste tereta: A i B. Masa jednoga komada tereta A iznosi 5 jed., a dobit ostvarena njegovim transportom iznosi 6 n.j. Masa jednoga komada tereta B iznosi 3 jed., a dobit ostvarena njegovim transportom iznosi 4 n.j. Tvrtka želi prevesti što više tereta obiju vrsta tako da ukupna ostvarena dobit bude maksimalna.

a) Formirajte matematički model promatranoga problema.

b) Nađite optimalan plan prijevoza i odgovarajuću optimalnu ostvarenu dobit.

c) Ako je optimalna količina neke vrste tereta jednaka nuli, istražite kako njezino povećanje za 1 komad utječe na optimalnu količinu druge vrste tereta.

d) Riješite podzadatke a) i b) uz dodatni uvjet da se kamionom može prevesti najviše 5 komada tereta B.

Rezultati: Neka su x_A i x_B redom prevezene količine tereta A i tereta B.

a) Matematički model glasi:

maksimizirati \(z= 6\cdot x_A + 4\cdot x_B\)

pod uvjetima

\(5\cdot x_A + 3\cdot x_B \le 45\),

\(x_A, x_B \in \mathbf{N}_0\).

b) \(\left( {x_A^*,x_B^*} \right) = (0,15)\), tj. optimalan plan prijevoza je prevesti samo točno 15 komada tereta B. Pripadna optimalna dobit iznosi z* = 60 n.j.

c) \(\left( {x_A^*,x_B^*} \right) = (1,13)\), pa povećanje optimalne količine tereta A za 1 komad uzrokuje smanjenje optimalne količine tereta B za 2 komada.

d) Matematički model glasi:

maksimizirati \(z = 6\cdot x_A + 4\cdot x_B\)

pod uvjetima

\(5\cdot x_A + 3\cdot x_B \le 45\),

x_A \(\in\) N₀, x_B \(\in\) [5]₀.

Rješavanjem se dobije \(\left( {x_A^*,x_B^*} \right) = (6,5)\), tj. optimalan plan prijevoza je prevesti točno 6 komada tereta A i točno 5 komada tereta B. Pripadna optimalna dobit iznosi z* = 56 n.j.

[1] S WEB-stranice http://www.wiley.com/college/tech/winqsb.htm može se ''skinuti'' besplatna verzija programa WinQSB

[2] Skraćenica za „novčanih jedinica“

[3] Osnovno o problemu naprtnjače može se naći u [1] , a detaljnije u [3] ili [6]

[4] Ako, eventualno, broj komada namirnice N_i nije definiran, možemo uzeti \({n_i}: = \frac{M}{{{m_i}}}\)

[5] Vrijednost namirnice obično se definira kao umnožak njezine mase (ili obujma) i jedinične cijene (tj. cijene po jedinici mase ili obujma)

[6] Pritom pretpostavljamo da su sve vrijednosti M, v_i i m_i nenegativne (to su tzv. prirodni uvjeti)

[7] Izomorfni problemi imaju isti matematički model i iste tipove varijabli, a razlikuju se eventualno u interpretaciji tih varijabli

[8] Istaknimo zasebno: Što – ako analiza ne daje optimalna rješenja problema koji sadrže uvjet tipa ''barem jedan…''. Opcija Preset Decision zahtijeva unos unaprijed zadane točne vrijednosti varijabli, a ne unose najmanje ili najveće vrijednosti bilo koje od varijabli

[9] Skraćenica za „kubičnih jedinica“

Kvantitativne metode odlučivanja – problem jednostavne razdiobe ulaganja

optimizacija

Bojan Kovačić i Tihana Strmečki, Tehničko veleučilište, Zagreb

Problemi razdiobe ulaganja općenito podrazumijevaju određivanje razdiobe određenoga novčanog iznosa na određeni broj gospodarskih grana tako da ukupna očekivana neto-dobit nastala tim ulaganjima bude maksimalna. U ovu kategoriju pripada i problem minimizacije troškova proizvodnje: ako u jednakim vremenskim intervalima treba proizvesti određenu količinu nekoga proizvoda i ako su poznati troškovi proizvodnje u svakom pojedinom intervalu, valja napraviti raspored proizvodnje tako da ukupni troškovi budu minimalni. Navedene probleme, njihovo matematičko modeliranje i rješavanje metodama dinamičkoga programiranja opisujemo na nizu primjera, pri čemu uz neke dajemo postupak rjeąavanja s pomoću računalnoga programa WinQSB.[1] Radi boljega razumijevanja navedenih metoda, navodimo objašnjenja njihovih osnovnih pojmova.

Dinamičko programiranje je metoda rješavanja složenih problema koji imaju određenu pravilnost u strukturi. Riječ programiranje dolazi iz vremena prije nastanka računalnog programiranja, a sinonim je riječi optimizacija. Koristi se u slučajevima u kojima problem ima optimalnu podstrukturu − mogućnost rastava na manje potprobleme iste vrste i neznatno razlikovanje potproblema od problema s nivoa iznad (problemi koji se svode na znatno manji potproblem rješavaju se drugim metodama). Rješavanju se može pristupati tehnikama „od vrha prema dnu“ ili „od dna prema vrhu“, pri čemu se dobiveni rezultati spremaju u tablicu za buduće korištenje, čime se izbjegava ponovno računanje. Traženo rješenje dobije se rekurzivno iz optimalnih rješenja potproblema, preko Bellmanove jednadžbe (Richard Bellman, 1953.). Ovakva metoda memoizacije puno je brža od metode u kojoj se svaki put nanovo rješava svaki manji korak, koji se ne javlja nužno prvi put.

Kod problema koji imaju računalnu primjenu, bitan je broj koraka implementacije danog zadatka. Manji broj koraka omogućuje brže i učinkovitije rješavanje, zbog čega je ocjenjivanje broja operacija važan kriterij za odabir načina rješavanja.

U primjerima ovoga članka korišteni su matematički modeli s cjelobrojnim koeficijentima i cjelobrojnim varijablama[2]. Zbog primijenjene metode dinamičkog programiranja nije moguće računanje s realnim brojevima. Međutim, u praksi se kao mjerne jedinice varijabli u modelu vrlo često pojavljuju desetine, stotine, tisuće i milijuni (novčanih jedinica ili proizvoda), što može znatno usporiti postupak rješavanja. U takvim slučajevima pogodno je redefinirati mjerne jedinice varijabli tako da se kao nova mjerna jedinica uzme neki višekratnički oblik polazne mjerne jedinice (npr. valutna jedinica 1000 kn umjesto valutne jedinice 1 kn). Osnovne prednosti takvoga redefiniranja su smanjenje ukupnoga broja potrebnih računskih operacija i povećavanje brzine izračuna optimalnoga rješenja, a osnovni nedostatak je smanjenje mogućnosti dobivanja preciznijih informacija o optimalnom rješenju. Naime, zbog cjelobrojnosti svih varijabli u matematičkom modelu, i optimalno rješenje je cjelobrojno, pa ćemo tako npr. u problemu čije je „stvarno“ optimalno rješenje x^* = 1234.56 [kn] odabirom valutne jedinice 1000 kn umjesto valutne jedinice 1 kn dobiti optimalno rješenje y^* = 1 [000 kn], tj. y^* = 1000 [kn] koje se bitno razlikuje od rješenja x*. Zbog toga prigodom eventualnoga redefiniranja mjernih jedinica treba odabrati što manje višekratničke oblike polaznih mjernih jedinica kako se ne bi izgubilo na preciznosti izračuna optimalnoga rješenja.

Spomenuti program WinQSB već pri odabiru numeričkih vrijednosti strogo većih od 500 pokazuje vlastita ograničenja i zahtijeva bitno dulje trajanje izračuna, pa je u primjeni toga programa redefiniranje mjernih jedinica pogodno u slučajevima u kojima je relativna većina svih numeričkih vrijednosti strogo veća od 500.[3] U Primjerima 4. i 6. posebno ćemo analizirati utjecaj takvoga redefiniranja na preciznost izračuna optimalnoga rješenja.

Radi kraćeg i jednostavnijeg zapisa, označavamo:

[n]₀ := {0, 1, 2… n} = prvih n + 1 elemenata skupa N₀ := {0, 1, 2…};

[n] := {1, 2… n} = skup prvih n prirodnih brojeva.

Primjer 1. Uprava neke tvrtke želi uložiti najviše 8 n.j.[4] u tri odjela te tvrtke tako da iznos svakoga pojedinog uloga bude cjelobrojan te da se u svaki odjel uloži najviše 5 n.j. (dakle, moguće je da se u neki odjel ne uloži ništa, kao i da se ne uloži sav predviđeni kapital.) Kriterij za razdiobu ulaganja su ostvarene neto-dobiti u pojedinim odjelima koje linearno ovise o iznosima uloženoga kapitala. Uloži li se po 1 n.j. u svaki odjel, prvi odjel ostvarit će neto-dobit od 4 n.j., drugi odjel neto-dobit od 5 n.j., a treći odjel neto-dobit od 2 n.j. Formirajmo odgovarajući matematički model, pa odredimo optimalan iznos ulaganja u svaki odjel tako da ukupna neto-dobit bude maksimalna.

Matematički model: Za svaki \(i\in [3]\) označimo s x_i iznos ulaganja u i–ti odjel. Ukupna neto-dobit D(x₁, x₂, x₃) nastala tim ulaganjima iznosi

D(x₁, x₂, x₃) = 4 × x₁ + 5 × x₂ + 2 × x₃.

Stoga je matematički model promatranoga problema:

maksimizirati D(x₁, x₂, x₃) = 4 × x₁ + 5 × x₂ + 2 × x₃

pod uvjetima

x₁ + x₂ + x₃≤ 8

x₁, x₂, x₃ ∈ [5]₀.

Analitičko rješenje: Traženi iznos možemo izračunati koristeći se tzv. pohlepnim principom: uzmemo najveći mogući kapital i uložimo najviše što možemo u profitabilniji od dvaju promatranih odjela, ostatak potom u manje profitabilan odjel itd. U ovom slučaju to znači da svih 8 n.j. ulažemo tako da maksimalno dopuštenih 5 n.j. uložimo u drugi (profitabilniji) odjel, a ostatak od 8 – 5 = 3 n.j. uložimo u prvi odjel, pa će ukupna optimalna neto-dobit iznositi 5 × 5 + 4 × 3 = 37 n.j.

Rješavamo li problem dinamičkim programiranjem, osnovna je ideja podijeliti problem u tri faze tako da se za svaki \(i\in [3]\), u i–toj fazi rješavanja promatra ulaganje kapitala u odjele 1… i pri čemu se u izračunima u dotičnoj fazi koriste optimalne vrijednosti dobivene u prethodnim fazama. Radi kraćega zapisa, označimo C := [8]₀.

Dakle, u prvoj fazi određujemo optimalnu neto-dobit kad se kapital ulaže samo u prvi odjel. Uz ulaganje 1 n.j. u prvi odjel ostvaruje se neto-dobit od 4 n.j., pa će za ulog od x₁ n.j. ostvarena neto-dobit iznositi 4 × x₁ n.j. Primijetimo da, zbog uvjeta zadatka, ne znamo točan iznos ukupno uloženoga kapitala, nego znamo jedino da je taj iznos neki prirodan broj najviše jednak 8 (ekvivalentno, ukupni uloženi kapital je neki element skupa C, ali ne znamo koji je to točno element). Stoga za svaki \(c \in C\) računamo vrijednosti realne funkcije \(f:C\to \mathbb{R}\) definirane s:

\(f_1\)(c) = 4 × c.

Te su vrijednosti, zapravo, optimalne neto-dobiti u slučaju kad ukupni kapital od c n.j. ulažemo samo u prvi odjel. Odmah napomenimo da za vrijednosti \(c \in C\) takve da je c ≥ 5 stavljamo \(f_1\)(c) = \(f_1\)(5) jer ukupno ulaganje u prvi odjel ne može biti strogo veće od 5 n.j. Tako dobivamo sljedeću tablicu:

c	\(f_1\)(c)	\({x_1}^*\)
0	0	0
1	4	1
2	8	2
3	12	3
4	16	4
5	20	5
6	20	5
7	20	5
8	20	5

Tablica 1. Optimalne vrijednosti funkcije \(f_1\)

Vrijednost \({x_1}^*\) označava optimalno ulaganje u prvi odjel za koje se postiže pripadna optimalna vrijednost \(f_1\)(c). U prvoj je fazi ovaj zapis praktički nepotreban, ali će nam poslužiti u sljedećim dvjema fazama.

U drugoj fazi razmatramo slučaj ulaganja kapitala samo u prvi i drugi odjel. Pretpostavimo da ukupno ulažemo c n.j., pri čemu je \(c\in C\). Za svaki \(i \in [2]\) označimo s x_i iznos koji ulažemo u i–ti odjel. Tada mora vrijediti jednakost

x₁ + x₂ = c,

iz koje je

x₁ = c – x₂.

Neto-dobit koju će ostvariti drugi odjel iznosi 5 × x₂ n.j., a optimalna neto-dobit koju će ostvariti prvi odjel, prema definiciji funkcije \(f_1\), iznosi \(f_1\)(x₁), tj. \(f_1\)(c – x₂) n.j. Stoga za svaki \(c \in C\) računamo vrijednosti realne funkcije \(f_2:C\to \mathbb{R}\) definirane s:

\[f_2(c)= \max_{\begin{subarray}{l} 0 \leqslant {x_2} \leqslant \min \left\{ {c,5} \right\} \\ {x_2} \in \mathbb{Z} \end{subarray}} \left[ {5 \cdot {x_2} + {f_1}(c - {x_2})} \right].\]

Te su vrijednosti, zapravo, optimalne neto-dobiti ako ukupni kapital od c n.j. uložimo samo u prvi i drugi odjel. Uvjeti pri kojima određujemo maksimum posljedice su zahtjeva da iznos x₂ mora biti cjelobrojan i ne smije premašiti niti ukupni kapital od c n.j., niti 5. n.j. Radi ilustracije postupka, prikazujemo izračun vrijednosti f₂(4) i f₂(8):

\[ f_2(4)=\max_{\begin{subarray}{l} 0 \leqslant {x_2} \leqslant \min \left\{ {4,5} \right\} \\ {x_2} \in \mathbb{Z} \end{subarray}} \left[ {5 \cdot {x_2} + {f_1}(4 - {x_2})} \right] = \max_{0 \leqslant {x_2} \leqslant 4} \left[ {5 \cdot {x_2} + {f_1}(4 - {x_2})} \right] = \] \( \max \{5 \cdot 0 + f_1(4 – 0), 5 \cdot 1 + f_1(4– 1), 5 \cdot 2 + f_1(4– 2), 5 \cdot 3 + f_1(4– 3), 5 \cdot 4 + f_1(4– 4)\} = \) \( \max \{0 + f_1(4), 5 + f_1(3), 10 + f_1(2), 15 + f_1(1), 20 + f_1(0)\} = \) \( \max \{0 + 16, 5 + 12, 10 + 8, 15 + 4, 20 + 0\} = 20; \)

\[ f_2(8)= \max_{\begin{subarray}{l} 0 \leqslant {x_2} \leqslant \min \left\{ {8,5} \right\} \\ {x_2} \in \mathbb{Z} \end{subarray}} \left[ {5 \cdot {x_2} + {f_1}(8 - {x_2})} \right] = \max_{0 \leqslant {x_2} \leqslant 5} \left[ {5 \cdot {x_2} + {f_1}(8 - {x_2})} \right] = \] \( \max \{5 \cdot 0 + f_1(8 – 0), 5 \cdot 1 + f_1(8 – 1), 5 \cdot 2 + f_1(8 – 2), 5 \cdot 3 + f_1(8 – 3), 5 \cdot 4 + f_1(8 – 4), 5 \cdot 5 + f_1(8 – 5)\} = \) \( \max \{0 + f_1(8), 5 + f_1(7), 10 + f_1(6),15 + f_1(5), 20 + f_1(4), 25 + f_1(3)\} = \) \( \max \{0 + 20, 5 + 20, 10 + 20, 15 + 20, 20 + 16, 25 + 12\} = 37.\)

Sve vrijednosti funkcija \(f_1\) i \(f_2\) navedene su u sljedećoj tablici:

c	\(f_1(c)\)	\(x_1^*\)	\(f_2(c)\)	\(x_2^*\)
0	0	0	0	0
1	4	1	5	1
2	8	2	10	2
3	12	3	15	3
4	16	4	20	4
5	20	5	25	5
6	20	5	29	5
7	20	5	33	5
8	20	5	37	5

Tablica 2. Optimalne vrijednosti funkcija \(f_1\) i \(f_2\)

Vrijednost \(x_2^*\) označava optimalno ulaganje u drugi odjel za koje se postiže pripadna optimalna vrijednost f₂(c). Npr. za c = 4 optimalna se vrijednost f₂(c) = f₂(4) = 20 postiže ulaganjem \(x_2^*\) = 4 n.j. u drugi odjel.

U trećoj fazi razmatramo ulaganje kapitala u sva tri odjela. Analogno kao u drugoj fazi, pretpostavimo da ulažemo ukupno c n.j. pri čemu je \(c\in C\). Za svaki \(i\in [3]\) označimo s x_i iznos uložen u i–ti odjel. Tada mora vrijediti jednakost

x₁ + x₂ + x₃ = c,

iz koje je

x₁ + x₂ = c – x₃.

Uložimo li u treći odjel x₃ n.j., neto-dobit koju će ostvariti taj odjel iznosi 2 × x₃ n.j., a optimalna neto-dobit koju će ostvariti prvi i drugi odjel zajedno, prema definiciji funkcije f₂, iznosi f₂(x₁ + x₂) n.j., odnosno f₂(c – x₃) n.j. Stoga za svaki \(c\in C\) računamo vrijednosti realne funkcije \(f_3:C\to \mathbb{R}\) definirane s

\[ f_3(c)= \max_{\begin{subarray}{l} 0 \leqslant {x_3} \leqslant \min \left\{ {c,5} \right\} \\ {x_3} \in \mathbb{Z} \end{subarray}} \left[ {2 \cdot {x_3} + {f_2}(c - {x_3})} \right].\]

Te su vrijednosti, zapravo, optimalne neto-dobiti ako ukupni kapital od c n.j. uložimo u sva tri odjela. Uvjeti pri kojima određujemo maksimum posljedica su zahtjeva da iznos x₃ mora biti cjelobrojan i ne smije premašiti niti ukupni kapital od c n.j., niti 5. n.j. Radi ilustracije postupka, prikazujemo izračun vrijednosti f₂(4) i f₂(8):

f₃(4) = \[ \max_{\begin{subarray}{l} 0 \leqslant {x_3} \leqslant \min \left\{ {4,5} \right\} \\ {x_3} \in \mathbb{Z} \end{subarray}} \left[ {2 \cdot {x_3} + {f_2}(4 - {x_3})} \right] = \max_{0 \leqslant {x_3} \leqslant 4} \left[ {2 \cdot {x_3} + {f_2}(4 - {x_3})} \right]\] = max {2 × 0 + f₂(4 – 0), 2 × 1 + + f₂(4 – 1), 2 × 2 + f₂(4 – 2), 2 × 3 + f₂(4 – 3), 2 × 4 + f₂(4 – 4)} = max {0 + f₂(4), 2 + f₂(3), 4 + + f₂(2), 6 + f₂(1), 8 + f₂(0)} = max {0 + 20, 2 + 15, 4 + 10, 6 + 5, 8 + 0} = 20;

f₃(8) = \[ \max_{\begin{subarray}{l} 0 \leqslant {x_3} \leqslant \min \left\{ {8,5} \right\} \\ {x_3} \in \mathbb{Z} \end{subarray}} \left[ {2 \cdot {x_3} + {f_2}(8 - {x_3})} \right] = \max_{0 \leqslant {x_3} \leqslant 5} \left[ {2 \cdot {x_3} + {f_2}(8 - {x_3})} \right]\] = max {2 × 0 + f₂(8 – 0), 2 × 1 + + f₂(8 – 1), 2 × 2 + f₂(8 – 2), 2 × 3 + f₂(8 – 3), 2 × 4 + f₂(8 – 4), 2 × 5 + f₂(8 – 5)} = max {0 + + f₂(8), 2 + f₂(7), 4 + f₂(6), 6 + f₂(5), 8 + f₂(4), 10 + f₂(3)} = max {0 + 37, 2 + 33, 4 + 29, 6 + + 25, 8 + 20, 10 + 15} = 37.

Svih 9 vrijednosti svake od triju promatranih funkcija pregledno su dane u sljedećoj tablici.

c	\(f_1(c)\)	\( x_1^*\)	f₂(c)	\( x_2^*\)	f₃(c)	\( x_3^*\)
0	0	0	0	0	0	0
1	4	1	5	1	5	0
2	8	2	10	2	10	0
3	12	3	15	3	15	0
4	16	4	20	4	20	0
5	20	5	25	5	25	0
6	20	5	29	5	29	0
7	20	5	33	5	33	0
8	20	5	37	5	37	0

Tablica 3. Optimalne vrijednosti funkcija \(f_1\), \(f_2\) i \(f_3\)

Optimalna vrijednost funkcije f₃ jednaka je 37 i postiže se za c = 8, što znači da se optimalna ukupna neto-dobit ostvaruje ulaganjem cjelokupnoga raspoloživog kapitala od 8 n.j. Odredimo pripadne optimalne iznose ulaganja u svaki odjel.

Vrijednost f₃(8) = 37 postiže se kao zbroj 0 + 37, odnosno kao zbroj 0 + f₂(8), tj. kao zbroj 2 × × 0 + f₂(8 – 0). Odatle ''očitavamo'' da je optimalna vrijednost varijable x₃ jednaka \(x_3^*\) = 0, pa zaključujemo da u treći odjel ne ulažemo ništa.

Vrijednost f₂(8) = 37 postiže se kao zbroj 25 + 12, odnosno kao zbroj 25 + f_1(3), tj. kao zbroj 5 × 5 + f_1(8 – 5). Odatle ''očitavamo'' da je optimalna vrijednost varijable x₂ jednaka \(x_2^*\) = 5, pa u drugi odjel ulažemo ukupno 5 n.j.

Vrijednost \(f_1(3) = 12\) postiže se kao umnožak 4 × 3, pa je optimalna vrijednost varijable x₁ jednaka \(x_1^*\) = 3, stoga u prvi odjel ulažemo ukupno 3 n.j.

Dobiveni optimalan plan ulaganja možemo pregledno prikazati sljedećom tablicom:

odjel	optimalan iznos ulaganja [n.j.]
1	3
2	5
3	0

Tablica 4. Optimalan plan ulaganja – rješenje Primjera 1

Pripadna optimalna neto-dobit iznosi 37 n.j.

Rješenje s pomoću programa WinQSB: Program WinQSB ne sadržava potprogram namijenjen rješavanju problema optimalne razdiobe ulaganja, ali sadržava potprogram Dynamic Programming (u daljnjem tekstu DP) namijenjen, među ostalim, rješavanju problema naprtnjače (ruksaka). Unutar njega ne postoje druge aplikacije pogodne za rješavanje promatranog problema. Ako je problem linearan, može se primijeniti potprogram Linear and Integer Programming, ali uz znatne restrikcije ulaznih podataka.

Prije nego što opišemo rješenje s pomoću programa WinQSB, ukratko ćemo navesti osnovna obilježja problema naprtnjače.

Problem naprtnjače (engl. the knapsack problem) česta je tema na području primijenjene matematike, financijske alokacije sredstava, kombinatorike i kriptografije. Naziv problema proizlazi iz narodne predaje: kako lopov s naprtnjačom određenog obujma može ukrasti predmete što veće vrijednosti[5], a da pritom obujam ukradenih predmeta ne premaši obujam naprtnjače? Prvi pisani tragovi o problemu datiraju iz 1897. godine, a u posljednjih nekoliko desetljeća jednako se intenzivno proučavaju i teorija i praktična primjena. Razlog tomu je modeliranje mnogih industrijskih, financijskih i kriptografskih problema preko problema naprtnjače, poput kapitalnog budžetiranja, ukrcavanja tereta, smanjivanja zaliha, izrade portfolija, kriptosustava itd.

Postoje tri osnovne podjele problema naprtnjače. Prva razlikuje slučajeve u kojima postoji jedna naprtnjača (single knapsack problem) od onih u kojima postoji više njih (multiple knapsack problem). Sljedeća podjela odnosi se na „djeljivost“ predmeta. U cjelobrojnom problemu naprtnjače predmeti su „nedjeljivi“, tj. ne možemo uzeti manji dio niti jednog predmeta, već samo predmet u cjelini. U djeljivom problemu naprtnjače predmeti se mogu razdijeliti na manje dijelove. U trećoj podjeli ograničen problem naprtnjače ograničava količinu svakog predmeta s nekom cjelobrojnom vrijednosti, dok neograničen problem naprtnjače ne postavlja nikakvu gornju granicu na broj komada pojedine vrste predmeta.

S obzirom na vrstu problema naprtnjače, može se primijeniti nekoliko različitih algoritama za rješavanje: pohlepni algoritam (engl. greedy algorithm), granice i grananje (engl. branch-and-bound), linearno programiranje, dinamičko programiranje i drugi. U programu WinQSB za rješavanje problema primjenjuje se dinamičko programiranje.

Tipičan problem naprtnjače je sljedeći:

Problem 1. Putnik ima naprtnjaču čija je najveća dopuštena nosivost M kg. Na odabir mu je ponuđeno ukupno n vrsta namirnica: N₁… N_n, pri čemu su sve namirnice međusobno ravnopravne. Za svaki i \in [n] neka su v_i i m_i redom vrijednost[6] i masa namirnice N_i. Kako putnik treba napuniti naprtnjaču namirnicama tako da ukupna masa svih namirnica stavljenih u naprtnjaču ne bude veća od M kg i da ukupna vrijednost tih namirnica bude što veća?[7]

Za svaki \(i \in [n] \) definiramo varijable \(x_i\) s:

\[{x_i} = \left\{ \begin{gathered} 0,{\text{ ako namirnicu }}{N_i}{\text{ ne stavljamo u naprtnjaču;}} \\ 1,{\text{ ako namirnicu }}{N_i}{\text{ stavljamo u naprtnjaču.}} \\ \end{gathered} \right.\]

Promatrani problem možemo opisati sljedećim matematičkim modelom:

maksimizirati \(f({x_1},...,{x_n}) = \sum\limits_{i = 1}^n {{w_i} \cdot {x_i}} \)

pod uvjetima

\[\begin{gathered} \sum\limits_{i = 1}^n {{a_i} \cdot {x_i} \leqslant M,} \\ {x_i} \in \left\{ {0,1} \right\}{\text{, za svaki }}i \in \left[ n \right] \end{gathered} \]

Ova najčešća i najpoznatija formulacija ograničenog cjelobrojnog problema naprtnjače poznata je kao 0 - 1 problem naprtnjače. Izraz „0-1“ potječe od interpretacije varijabli x_i: svaki predmet ili se uzima u cijelosti ili se uopće ne uzima.

S obzirom na to da imamo n vrsta namirnica, postoji ukupno \(2^n\) različitih mogućnosti odabira. Jedan od načina određivanja optimalne mogućnosti je ispitivanje svih kombinacija. Za to bi nam trebalo \(O({2^n})\) operacija, što najčešće nije najbolje moguće vrijeme. Uz korištenje dinamičkog programiranja, rješavanje promatranoga problema može se svesti na pseudopolinomijalno (u ovisnosti o \(C_0\)).

Problem iz Primjera 1 možemo ''prevesti'' na sljedeći zatvoreni problem naprtnjače:

Na raspolaganju nam je po 5 komada svake od triju vrsta namirnica: N₁, N₂ i N₃ te naprtnjača kapaciteta 8 kg. Podaci o jediničnoj cijeni i jediničnoj masi svake namirnice navedeni su u donjoj tablici.

namirnica	jedinična cijena [n.j.]	jedinična masa [kg]
N₁	4	1
N₂	5	1
N₃	2	1

Tablica 5. Ulazni podaci za zatvoreni problem naprtnjače

Treba odabrati namirnice što veće ukupne vrijednosti tako da njihova ukupna masa ne bude veća od kapaciteta naprtnjače. Formirajmo odgovarajući matematički model, pa odredimo optimalan izbor namirnica i pripadnu optimalnu ukupnu vrijednost.

Ovako definiran problem ima isti matematički model kao i polazni problem, ali s drugačijim interpretacijama varijabli, funkcije cilja i uvjeta. Takvi se problemi uobičajeno nazivaju izomorfnima: njihovi matematički modeli su jednaki do na interpretacije ulaznih i izlaznih varijabli[8] te se rješavaju istim metodama/algoritmima.

Pokretanjem potprograma DP odaberimo tip Knapsack Problem (vidjeti Sliku 1).

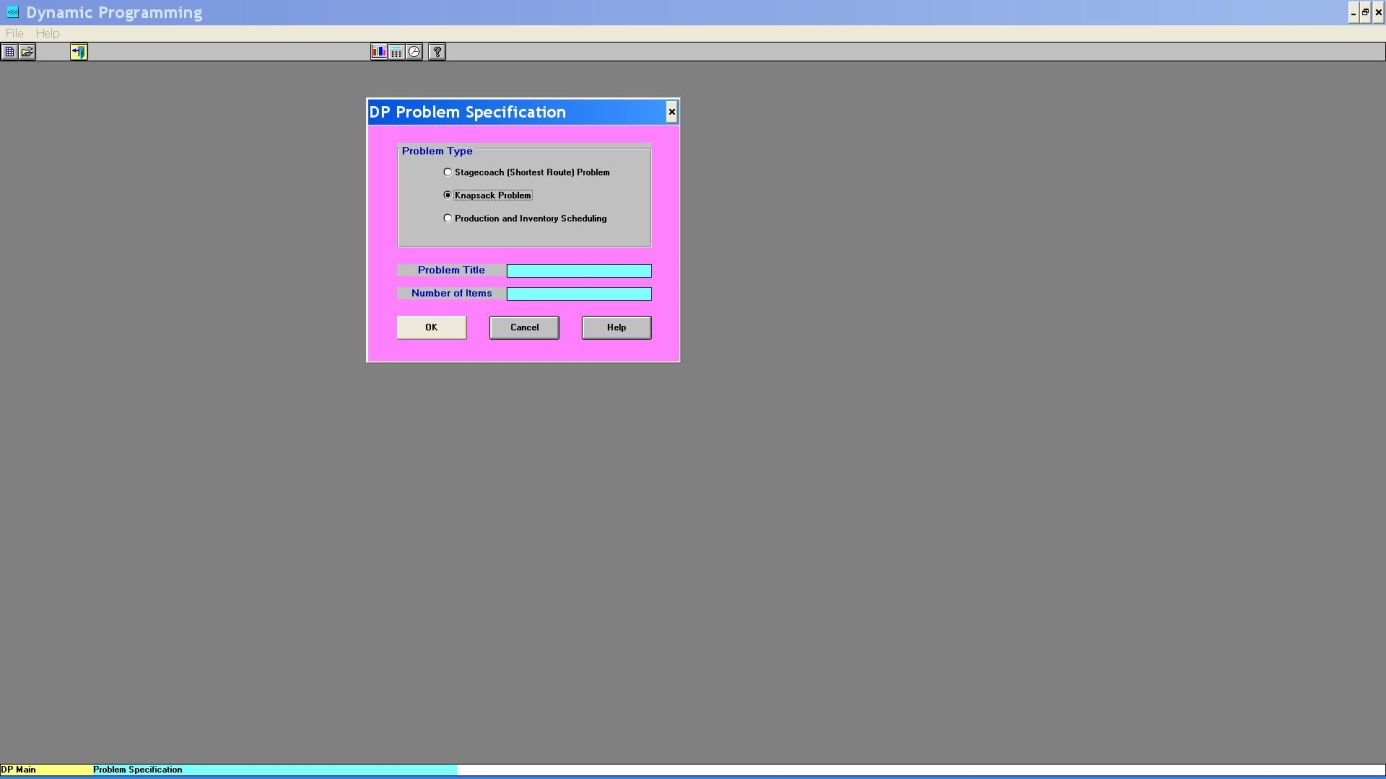
Slika 1. Dijaloški okvir potprograma DP

Nazovimo problem koji ćemo rješavati Primjer 1, tj. upišimo:

Problem Title: Primjer 1

Number of Items: 3

Potom kliknimo na OK. U sljedećem koraku unosimo ulazne podatke (vidjeti Sliku 2).

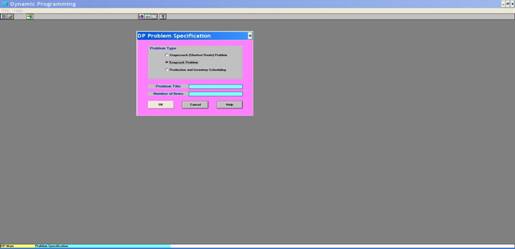
Slika 2. Unos ulaznih podataka

U drugi stupac (Item Identification) upišimo redom O1, O2 i O3 jer će nam takve oznake na kraju ''otkriti'' svotu uloženu u svaki pojedini odjel.

U treći stupac (Units Available) upisujemo najveći mogući iznos koji može biti uložen u svaki pojedini odjel. Ti iznosi su jednaki 5, pa upisujemo: 5, 5, 5.

U četvrti stupac (Unit Capacity Required) treba upisati koeficijente uz nepoznanice x₁, x₂ i x₃ u uvjetu x₁ + x₂ + x₃ £ 8. Oni su jednaki 1, pa u četvrti stupac upišimo: 1, 1, 1. Istaknimo odmah da su prigodom modeliranja problema jednostavne razdiobe ulaganja koeficijenti u ovom stupcu uvijek jednaki 1, dok kod problema složene razdiobe ulaganja (obrađenoga u točki 1.4.) ti koeficijenti općenito mogu biti i nenegativni realni brojevi različiti od 1.

U peti stupac (Return Function (X: Item ID)) upišimo redom komponente funkcije cilja koje se odnose na odjel iz pripadnoga retka. Tako u prvi redak toga stupca upišimo 4*X, u drugi 5*X, a u treći 2*X.

U posljednji redak pored natpisa Capacity= upišimo ukupan iznos kapitala, tj. 8.

Ovime je unos ulaznih podataka završen. Kliknimo lijevom tipkom miša na izbornik Solve and Analyze i odaberimo opciju Solve the Problem. Dobivamo izlaznu tablicu sa svim potrebnim rezultatima (vidjeti Sliku 3).

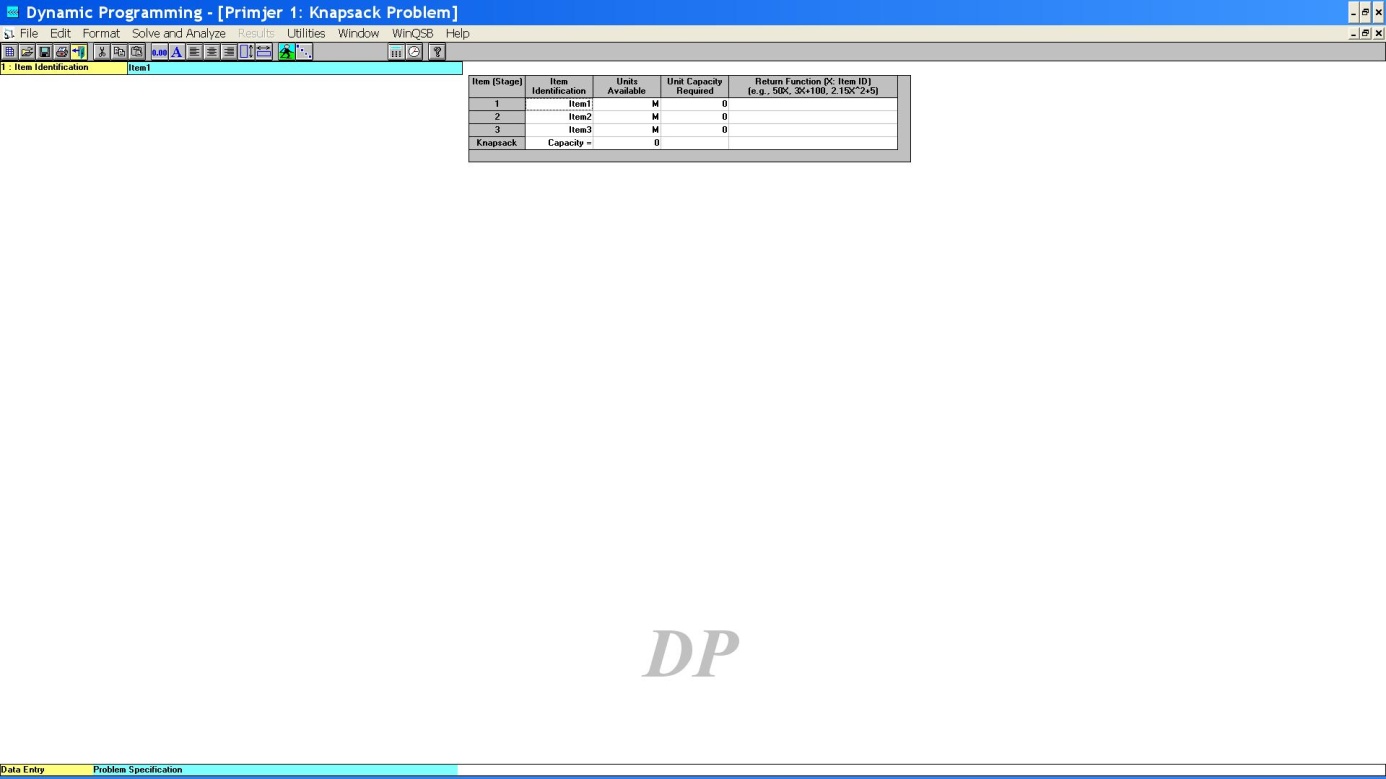
Slika 3. Izlazna tablica u Primjeru 1

Iz trećega stupca (Decision Quantity (X)) očitavamo optimalan iznos ulaganja u svaki pojedini odjel: u prvi odjel (O₁) treba uložiti 3 n.j., u drugi odjel (O₂) 5 n.j., dok se u treći odjel (O₃) ne ulaže ništa. Optimalnu neto-dobit očitavamo iz posljednjega retka (Total Return Value) i ona iznosi 37. n.j.

Na navedenom primjeru može se vidjeti i razlog naziva jednostavna razdioba ulaganja. Cjelokupni kapital dijeli se na međusobno ravnopravne dijelove, tj. na početku nemamo razloga preferirati bilo koji odjel tvrtke. Zbog toga se u uvjetu koji označava da zbroj svih uloženih iznosa mora biti najviše jednak predviđenom kapitalu uz nepoznanice koje označavaju uložene iznose kao koeficijenti pojavljuju jedinice. U gospodarskoj su praksi, međutim, mogući i slučajevi kad se na početku, prema nekom kriteriju, rangiraju ulaganja, pa se u takvim slučajevima govori o složenoj razdiobi ulaganja u kojoj se pojavljuju tzv. težinski koeficijenti. O time se više može naći npr. u [6].

Primjer 2. Problem optimalnog ulaganja kapitala u razvoj određene regije ili određene gospodarske grane može se definirati na sljedeći način: Za ostvarivanje bržega razvoja određene gospodarske grane predviđen je kapital u iznosu od C₀ n.j. Taj kapital može se uložiti u ukupno n različitih tvrtki iz navedene gospodarske grane. Ovisno o uloženom kapitalu, svaka pojedina tvrtka ostvarit će dodatnu neto-dobit (razliku ukupne neto-dobiti i uloženoga kapitala). Treba naći razdiobu raspoloživoga kapitala na navedene tvrtke tako da ukupna dodatna neto-dobit (tj. zbroj dodatnih neto-dobiti svih n tvrtki) bude maksimalna.

Konkretno, za ostvarivanje bržega razvoja određene gospodarske grane predviđen je kapital u iznosu od C₀ = 4.000.000,00 kn. Taj se kapital ulaže u ukupno tri tvrtke − T₁, T₂ i T₃ − pri čemu se u svaku tvrtku ili ne ulaže ništa ili se ulaže iznos koji je višekratnik broja 1.000.000 (nije nužno uložiti sav predviđeni kapital). Očekivana dodatna neto-dobit koju će ostvariti svaka tvrtka navedena je u sljedećoj tablici.

iznos ulaganja (milijuna kn)	očekivana dodatna neto-dobit tvrtke (milijuna kn)
iznos ulaganja (milijuna kn)	T₁	T₂	T₃
0	0	0	0
1	0.3	0.29	0.31
2	0.47	0.45	0.46
3	0.7	0.67	0.74
4	0.83	0.82	0.8

Tablica 6. Ulazni podaci za Primjer 2

a) Odredimo opći matematički model promatranoga problema uz pretpostavku da svi iznosi ulaganja nužno moraju biti cjelobrojni (moguće je da se u neku tvrtku ne uloži ništa).

b) Za konkretni slučaj nađimo optimalnu razdiobu predviđenoga kapitala.

Opći matematički model: Za svaki \(i\in [n] \) označimo s x_i iznos ulaganja u tvrtku T_i, a f_i(x_i) pripadnu očekivanu dodatnu neto-dobit [9]. Tada je ukupna očekivana dodatna neto-dobit od ulaganja u svih n tvrtki jednaka

f(x₁, x₂… x_n) = f₁(x₁) + f₂(x₂) +… + f_n(x_n) = \(\sum\limits_{i = 1}^n {{f_i}({x_i})} \)

pa zahtijevamo da vrijednost te funkcije bude maksimalna. Pogledajmo pripadne uvjete uz koje tražimo maksimalnu vrijednost. Zbroj svih ulaganja ne smije biti strogo veći od ukupnoga iznosa raspoloživoga kapitala C₀, pa mora vrijediti nejednakost

tj.

\( \sum\limits_{i = 1}^n {{x_i}}\le C_0\).

Iznos svakog ulaganja nužno mora biti cjelobrojan, a prema prirodi problema on mora biti i nenegativan i najviše jednak C₀. Zbog toga mora vrijediti:

x_i \in [C₀]₀, za svaki \(i \in [n]\).

Prema tome, traženi matematički model je:

maksimizirati f(x₁, x₂… x_n) = \(\sum\limits_{i = 1}^n {{f_i}({x_i})} \)

pod uvjetima

\(\sum\limits_{i = 1}^n {{x_i}} \le C_0\)

\(x_i \in \) [C₀]₀, za svaki \(i \in [n]\).

b) U konkretnom su slučaju n = 3 i C₀ = 4.[10] Odgovarajući matematički model je:

maksimizirati f(x₁, x₂, x₃) = f₁(x₁) + f₂(x₂) + f₃(x₃)

pod uvjetima

\(x_i \in [4]_0 \), za svaki \(i \in [3]\).

Stavimo C := [4]₀. Intuitivno možemo naslutiti da će se optimalna vrijednost postići bude li uloženi iznos jednak C₀. Problem ćemo riješiti u ukupno tri faze.

U prvoj fazi definirajmo realnu funkciju \(d_1:C\to \mathbb{R}\)

d₁(c) = \(f_1\)(c).

d₁(c) je zapravo optimalna očekivana dodatna neto-dobit ako se ukupan iznos od c milijuna kuna uloži isključivo u tvrtku T₁. Ti iznosi već su zadani u Tablici 6, pa ih pregledno prepišimo u sljedeću tablicu:

c	d₁(c)	\(x_1^*\)
0	0	0
1	0.3	1
2	0.47	2
3	0.7	3
4	0.83	4

Tablica 7. Rezultati prve faze rješenja Primjera 2

Vrijednost \(x_1^*\) označava optimalno ulaganje u tvrtku T₁ uz koju se postiže optimalna očekivana dodatna neto-dobit d₁(c). U ovom slučaju za svaki \(c\in C\) vrijedi jednakost \(x_1^* = c\), ali, kako smo vidjeli u Primjeru 1, u prvoj fazi ta jednakost općenito ne mora vrijediti.

U drugoj fazi definirajmo realnu funkciju \(d_2:C\to \mathbb{R}\) s:

d₂(c) =\( \max\limits_{\begin{subarray}{l} 0 \leqslant {x_2} \leqslant c \\ {x_2} \in C \end{subarray}} \left[ {{f_2}({x_2}) + {d_1}(c - {x_2})} \right]\).

d₂(c) je zapravo optimalna očekivana dodatna neto-dobit ako se ukupan iznos od c milijuna kuna uloži samo u tvrtke T₁ i T₂. Uloži li se iznos od x₂ milijuna kuna u tvrtku T₂, očekivana dodatna neto-dobit tvrtke T₂ iznosit će f₂(x₂). Preostali iznos od c – x₂ milijuna kuna ulaže se u tvrtku T₁, a prema definiciji funkcije d₁, optimalna očekivana dodatna neto-dobit nastala tim ulaganjem jednaka je d₁(c – x₂). Zbroj tih dviju očekivanih dodatnih neto-dobiti treba maksimizirati, pa odatle slijedi izraz iz definicije funkcije d₂.

Detaljno prikazujemo izračun vrijednosti d₂(4):

\[ d_2(4)= \max_{\begin{subarray}{l} 0 \leqslant {x_2} \leqslant 4 \\ x_2 \in C \end{subarray}} \left[ {{f_2}({x_2}) + {d_1}(4 - {x_2})} \right]= \max_{x_2 \in C} \left[ {{f_2}({x_2}) + {d_1}(4 - {x_2})} \right]=\] max{f₂(0) + d₁(4 – 0), f₂(1) + + d₁(4 – 1), f₂(2) + d₁(4 – 2), f₂(3) + d₁(4 – 3), f₂(4) + d₁(4 – 4)} = max{0 + 0.83, 0.29 + 0.7, 0.45 + 0.47, 0.67 + 0.3, 0.82 + 0} = 0.99.

Radi potpunosti razmatranja, u sljedećoj tablici navodimo i vrijednosti funkcije d₂ za preostale vrijednosti varijable c:

c	d₁(c)	\(x_1^*\)	d₂(c)	\(x_2^*\)
0	0	0	0	0
1	0.3	1	0.3	0
2	0.47	2	0.59	1
3	0.7	3	0.76	1
4	0.83	4	0.99	1

Tablica 8. Rezultati prvih dviju faza rješenja Primjera 2

Vrijednost \(x_2^*\) označava optimalno ulaganje u tvrtku T₂ uz koju se postiže optimalna očekivana dodatna neto-dobit d₂(c). To optimalno ulaganje ''očitava'' se iz postupka izračuna vrijednosti funkcije d₂. Npr. d₂(4) = 0.99 dobiva se kao zbroj 0.29 + 0.7, tj. kao zbroj f₂(1) + d₁(4 – 1). Odatle slijedi \(x_2^* = 1\) (i, naravno, \(x_1^* = 4 - x_2^* = 4 - 1 = 3\)) .

U trećoj fazi definirajmo realnu funkciju \(d_3\to \mathbb{R}\) s

d₃(c) =\( \max\limits_{\begin{subarray}{l} 0 \leqslant {x_3} \leqslant c \\ {x_3} \in C \end{subarray}} \left[ {{f_3}({x_3}) + {d_2}(c - {x_3})} \right]\).

d₃(c) je zapravo optimalna očekivana dodatna neto-dobit ako se ukupan iznos od c milijuna kuna uloži u sve tri tvrtke. Uloži li se iznos od x₃ milijuna kuna u tvrtku T₃, očekivana dodatna neto-dobit tvrtke T₃ iznosit će f₃(c). Preostali iznos od c – x₃ milijuna kuna ulaže se u tvrtke T₁ i T₂, a prema definiciji funkcije d₂, optimalna očekivana dodatna neto-dobit nastala tim ulaganjem jednaka je d₂(c – x₃). Zbroj tih dviju očekivanih dodatnih neto-dobiti treba maksimizirati, pa odatle slijedi izraz iz definicije funkcije d₃.

Detaljno prikazujemo izračun vrijednosti d₃(4):

\[ d_3(4) = \max_{\begin{subarray}{l} 0 \leqslant {x_3} \leqslant 4 \\ {x_3} \in C \end{subarray}} \left[ {{f_3}({x_3}) + {d_2}(4 - {x_3})} \right] = \max_{\begin{subarray}{l} 0 \leqslant {x_3} \leqslant 4 \\ {x_3} \in C \end{subarray}} \left[ {{f_3}({x_3}) + {d_2}(4 - {x_3})} \right]= \] max{f₃(0) + d₂(4 – 0), f₃(1) + d₂(4 – 1), f₃(2) + d₂(4 – 2), f₃(3) + d₂(4 – 3), f₃(4) + d₂(4 – 4)} = max{0 + 0.99, 0.31 + 0.76, 0.46 + 0.59, 0.74 + 0.3, 0.8 + 0} = 1.07.

Radi potpunosti razmatranja, u sljedećoj tablici navodimo i vrijednosti funkcije d₃ za preostale vrijednosti varijable c:

c	d₁(c)	\(x_1^*\)	d₂(c)	\(x_2^*\)	d₃(c)	\(x_3^*\)
0	0	0	0	0	0	0
1	0.3	1	0.3	0	0.31	1
2	0.47	2	0.59	1	0.61	1
3	0.7	3	0.76	1	0.90	1
4	0.83	4	0.99	1	1.07	1

Tablica 9. Rezultati svih triju faza rješenja Primjera 2

Iz Tablice 9 vidimo da se najveća vrijednost funkcije d₃, kako smo i očekivali, postiže za c = 4. Dakle, treba uložiti sav predviđeni kapital od 4.000.000,00 kn. Pripadni optimalni plan ulaganja ''očitava'' se iz postupaka izračuna vrijednosti funkcija d₁, d₂ i d₃ na sljedeći način:

Optimalna vrijednost d₃(4) = 1.07 dobiva se kao zbroj 0.31 + 0.76, tj. kao zbroj f₃(1) + d₂(4 – 1). Odatle slijedi \(x_3^* = 1\). Optimalna vrijednost d₂(4 – 1) = d₂(3) = 0.76 dobiva se kao zbroj 0.29 + 0.47, tj. kao zbroj f₂(1) + d₁(3 – 1). Odatle slijedi \(x_2^* = 1\) i \(x_1^* = 3 - 1 = 2\). Tražena optimalna razdioba kapitala navedena je u Tablici 10.

Tvrtka	optimalan iznos ulaganja (milijuna kn)
T₁	2
T₂	1
T₃	1

Tablica 10. Rješenje Primjera 2

Pripadna optimalna očekivana dodatna neto-dobit iznosi 1.070.000,00 kn.

Kako je istaknuto u uvodu, na problem optimizacije jednostavne razdiobe ulaganja mogu se svesti različiti problemi minimizacije ukupnih troškova proizvodnje nekoga proizvoda. Pokažimo to na primjerima.

Primjer 3. Tijekom tri mjeseca treba proizvesti točno 12 komada nekoga proizvoda, pri čemu je najveći mogući kapacitet proizvodnje 6 komada proizvoda mjesečno (moguće je da se u nekom mjesecu ne proizvede niti jedan proizvod). Troškovi proizvodnje upravno su razmjerni kvadratima broja proizvedenih proizvoda, te za svaki \( i \in [3]\) vrijedi: ako se u i–tom mjesecu proizvede x_i komada proizvoda, troškovi proizvodnje iznose w_i × \(x_i^2\) n.j., gdje su w_i strogo pozitivni realni parametri. Treba odrediti plan proizvodnje takav da ukupni troškovi proizvodnje budu minimalni.

a) Odredimo opći matematički model promatranoga problema.

b) Riješimo problem za konkretne vrijednosti: w₁ = 10, w₂ = 24 i w₃ = 32.

Matematički model: U postavci problema već je naznačeno da s x_i označavamo količinu (broj komada) proizvoda proizvedenu u i–tom mjesecu. Ukupan zbroj svih količina mora biti jednak 12, pa vrijedi jednakost:

x₁ + x₂ + x₃ = 12.

Troškovi proizvodnje u prvom mjesecu su \(w_1\cdot x_1^2\), troškovi proizvodnje u drugom mjesecu \(w_2\cdot x_2^2\), a troškovi proizvodnje u trećem mjesecu \(w_3\cdot x_3^2\). Stoga ukupni troškovi proizvodnje u navedena tri mjeseca iznose

f(x₁, x₂, x₃) = \( w_1\cdot x_1^2 + w_2\cdot x_2^2+ w_3\cdot x_3^2\).

Nadalje, iz tipa promatranoga problema slijedi da vrijednosti varijabli x_i nužno moraju biti elementi skupa N₀. Također, te vrijednosti ne smiju biti strogo veće od 6 jer je najveći mogući kapacitet proizvodnje jednak 6. Prema tome, matematički model promatranoga problema glasi:

minimizirati f(x₁, x₂, x₃) = \( w_1\cdot x_1^2 + w_2\cdot x_2^2+ w_3\cdot x_3^2\)

pod uvjetima

x₁ + x₂ + x₃ = 12,

\( x_1,x_2,x_3 \in [6]_0\).

Analitičko rješenje: Za w₁ = 10, w₂ = 24 i w₃ = 32 dobivamo sljedeći problem:

minimizirati f(x₁, x₂, x₃) = \( 10\cdot x_1^2 + 24\cdot x_2^2+ 32\cdot x_3^2\)

pod uvjetima

x₁ + x₂ + x₃ = 12,

\(x_1,x_2,x_3 \in [6]_0\).

I ovdje bismo mogli razmišljati ''pohlepno'', tj. da u prvom mjesecu treba proizvesti točno 6 komada proizvoda (jer su najmanji troškovi proizvodnje upravo u tom mjesecu), a u drugom preostalih 6 (jer su troškovi proizvodnje u drugom mjesecu manji nego u trećem). Stoga bi traženi plan mogao biti \(x_1^*\) = \(x_2^*\) = 6, \(x_3^*\)= 0, a minimalni troškovi f(6, 6, 0) = 10 × 6² + 24 × 6² + 32 × 0² = 1224 n.j. Pokazat ćemo, međutim, da ovakav ''pohlepni'' pristup u ovom slučaju ne daje optimalno rješenje.

Analogno prethodnim primjerima, stavimo C := [12]₀. Primijetimo da u ovom primjeru unaprijed znamo točan ukupan broj komada proizvoda koje treba proizvesti (to je 12), ali, radi ilustriranja tehnike dinamičkoga programiranja, u svakoj ćemo fazi rješavanja problema izračunavati 13 odgovarajućih vrijednosti.

U prvoj fazi za svaki \(c\in C\) računamo vrijednosti realne funkcije \(f_1:C\to \mathbb{R}\) definirane s:

\(f_1(c)=10\cdot c^2 \).

Vrijednosti funkcije \(f_1\) su optimalni troškovi proizvodnje ako se u prvom mjesecu proizvede točno c komada proizvoda. Pritom za svaki \(c\in C\) takav da je \(s\ge 7\) dogovorno stavljamo da su troškovi proizvodnje beskonačni jer je najveći proizvodni kapacitet, prema uvjetima zadatka, jednak 6. Tako dobivamo sljedeću tablicu:

c	\(f_1(c)\)	\(x_1^*\)
0	0	0
1	10	1
2	40	2
3	90	3
4	160	4
5	250	5
6	360	6
7	\(\infty\)	6
8	\(\infty\)	6
9	\(\infty\)	6
10	\(\infty\)	6
11	\(\infty\)	6
12	\(\infty\)	6

Tablica 11. Rezultati prve faze rješenja Primjera 3

Vrijednost \(x_1^*\) označava optimalnu proizvodnju u prvom mjesecu za koju se postiže pripadna optimalna vrijednost \(f_1(c)\). Pritom smo u retcima u kojima je \(f_1(c) = \infty\) dogovorno pisali \(x_1^*\) = 6 zbog već istaknute činjenice da je najveći mjesečni proizvodni kapacitet jednak 6.

U drugoj fazi računamo vrijednosti realne funkcije \(f_2:C\to\mathbb{R}\) definirane s:

U ovoj fazi pretpostavljamo da se ukupno c komada proizvoda mora proizvesti u prva dva mjeseca. Ako se u drugom mjesecu proizvede x₂ proizvoda, u prvom se mora proizvesti ukupno c – x₂ proizvoda. Troškovi proizvodnje u drugom mjesecu iznose 24 × \(x_2^2\) n.j., dok optimalni troškovi proizvodnje u prvom mjesecu, prema definiciji funkcije \(f_1\), iznose \(f_1(c-x_2)\) n.j. Zbroj tih troškova jednak je ukupnim troškovima proizvodnje u prva dva mjeseca, pa taj zbroj treba minimizirati imajući na umu uvjete da vrijednost varijable x₂ mora biti cjelobrojna, ne veća od ukupne količine proizvoda koju treba proizvesti i ne veća od najvećega mjesečnog kapaciteta proizvodnje. Odatle slijedi izraz iz definicije funkcije f₂.

Radi ilustracije, izračunat ćemo f₂(6) i f₂(12), pri čemu koristimo da vrijednosti \(f_1(7), f_1(8),\ldots, f_1(12)\) ne postoje jer se niti u jednom mjesecu (pa posebno niti u prvom mjesecu) ne može proizvesti strogo više od 6 komada proizvoda:

\[ f_2(6)= \min_{\begin{subarray}{l} 0 \leqslant x_2 \leqslant \min \left\{ 6,6 \right\} \\ x_2 \in \mathbb{Z} \end{subarray}} \left[ {24 \cdot x_2^2 + {f_1}(6 - {x_2})} \right] = \min_{0 \leqslant {x_2} \leqslant 6} \left[ {24 \cdot x_2^2 + {f_1}(6 - {x_2})} \right] = \] min {24 × 0² + f_1(6 – 0), 24 × 1² + f_1(6 – 1), 24 × 2² + f_1(6 – 2), 24 × 3² + f_1(6 – 3), 24 × 4² + f_1(6 – 4), 24 × 5² + f_1(6 – 5), 24 × 6² + f_1(6 – 6)} = min {0 + 360, 24 + 250, 96 + 160, 216 + 90, 384 + 40, 600 + 10, 864 + + 0} = 256;

\[ f_2(12) = \min_{\begin{subarray}{l} 0 \leqslant {x_2} \leqslant \min \left\{ {12,6} \right\} \\ {x_2} \in \mathbb{Z} \end{subarray}} \left[ {24 \cdot x_2^2 + {f_1}(12 - {x_2})} \right] = \min_{0 \leqslant {x_2} \leqslant 6} \left[ {24 \cdot x_2^2 + {f_1}(12 - {x_2})} \right] = \] min {24 × 0² + f_1(12 – 0), 24 × 1² + f_1(12 – 1), 24 × 2² + f_1(12 – 2), 24 × 3² + f_1(12 – 3), 24 × 4² + f_1(12 – 4), 24 × 5² + + f_1(12 – 5), 24 × 6² + f_1(12 – 6)} = min{24 × 6² + f_1(6)} = 1224.

Izračunom ostalih vrijednosti dobivamo sljedeću tablicu:

c	\(f_1(c)\)	\(x_1^*\)	f₂(c)	\(x_2^*\)
0	0	0	0	0
1	10	1	10	0
2	40	2	34	1
3	90	3	64	1
4	160	4	114	1
5	250	5	184	1
6	360	6	256	2
7	\(\infty\)	6	346	2
8	\(\infty\)	6	456	2
9	\(\infty\)	6	576	3
10	\(\infty\)	6	744	4
11	\(\infty\)	6	960	5
12	\(\infty\)	6	1224	6

Tablica 12. Rezultati prve i druge faze rješenja Primjera 3

Vrijednost \(x_2^*\) označava optimalnu proizvodnju u drugom mjesecu za koju se postiže pripadna optimalna vrijednost f₂(c), a može se ''očitati'' iz odgovarajućega izračuna vrijednosti f₂(c). Npr., f₂(6) = 256 dobiva se kao zbroj 96 + 160, tj. kao 24 · 2² + f₁(6 – 2). Odatle slijedi \(x_2^*\) = 2 i \(x_1^*\) = 6 – 2 = 4.

U trećoj fazi računamo vrijednosti realne funkcije \(f_3:C\to \mathbb{R}\) definirane s :

f₃(c) =\( \min\limits_{\begin{subarray}{l} 0 \leqslant {x_3} \leqslant \min \left\{ {c,6} \right\} \\ {x_3} \in \mathbb{Z} \end{subarray}} \left[ {32 \cdot x_3^2 + {f_2}(c - {x_3})} \right]\).

U ovoj fazi, pretpostavljamo, treba proizvesti ukupno c komada proizvoda u sva tri mjeseca. Ako se u trećem mjesecu proizvede x₃ proizvoda, u prva dva mjeseca treba proizvesti ukupno c – x₃ proizvoda. Ukupni troškovi proizvodnje u trećem mjesecu iznose 32 × \(x_3^2\) n.j., dok optimalni troškovi proizvodnje u prva dva mjeseca, u skladu s definicijom funkcije f₂, iznose f₂(c – x₃) n.j. Stoga ukupni troškovi proizvodnje u sva tri mjeseca iznose 32 × \(x_3^2\) + f₂(c – x₃) n.j, pa taj zbroj treba minimizirati imajući na umu početne uvjete na vrijednost varijable x₃ (cijeli broj ne veći od ukupne količine proizvoda koju treba proizvesti i najvećega mjesečnog kapaciteta proizvodnje). Radi ilustracije postupka izračuna, detaljno prikazujemo izračun vrijednosti f₃(6) i f₃(12):

\[ f_3(6)= \min_{\begin{subarray}{l} 0 \leqslant {x_3} \leqslant \min \left\{ {6,6} \right\} \\ {x_3} \in \mathbb{Z} \end{subarray}} \left[ {32 \cdot x_3^2 + {f_2}(6 - {x_3})} \right] = \min_{\begin{subarray}{l} 0 \leqslant {x_3} \leqslant 6 \\ {x_3} \in \mathbb{Z} \end{subarray}} \left[ {32 \cdot x_3^2 + {f_2}(6 - {x_3})} \right] = \] min {32 × 0² + f₂(6 – 0), 32 × 1² + f₂(6 – 1), 32 × 2² + f₂(6 – 2), 32 × 3² + f₂(6 – 3), 32 × 4² + f₂(6 – 4), 32 × 5² + f₂(6 – 5), 32 × 6² + f₂(6 – 6)} = min {256, 216, 242, 352, 546, 810, 1152} = 216;

\[ f_3(12)= \min_{\begin{subarray}{l} 0 \leqslant {x_3} \leqslant \min \left\{ {12,6} \right\} \\ {x_3} \in \mathbb{Z} \end{subarray}} \left[ {32 \cdot x_3^2 + {f_2}(12 - {x_3})} \right] = \min_{\begin{subarray}{l} 0 \leqslant {x_3} \leqslant 6 \\ {x_3} \in \mathbb{Z} \end{subarray}} \left[ {32 \cdot x_3^2 + {f_2}(12 - {x_3})} \right] = \] min {32 × 0² + f₂(12 – – 0), 32 × 1² + f₂(12 – 1), 32 × 2² + f₂(12 – 2), 32 × 3² + f₂(12 – 3), 32 × 4² + f₂(12 – 4), 32 × 5² + + f₂(12 – 5), 32 × 6² + f₂(12 – 6)} = min {1224, 992, 872, 864, 968, 1146, 1408} = 864.

Izračunom svih vrijednosti funkcije f₃ dobivamo sljedeću tablicu:

c	\( f_1(c)\)	\(x_1^*\)	f₂(c)	\(x_2^*\)	f₃(c)	\(x_3^*\)
0	0	0	0	0	0	0
1	10	1	10	0	10	0
2	40	2	34	1	34	0
3	90	3	64	1	64	0
4	160	4	114	1	96	1
5	250	5	184	1	146	1
6	360	6	256	2	216	1
7	\(\infty\)	6	346	2	288	1
8	\(\infty\)	6	456	2	378	1
9	\(\infty\)	6	576	3	474	2
10	\(\infty\)	6	744	4	584	2
11	\(\infty\)	6	960	5	704	2
12	\(\infty\)	6	1224	6	864	3

Tablica 13. Rezultati svih triju faza rješenja Primjera 3

Vrijednost \(x_3^*\) označava optimalnu proizvodnju u trećem mjesecu za koju se postiže pripadna optimalna vrijednost f₃(c), a ''očitava'' se iz odgovarajućeg izračuna vrijednosti funkcije f₃. Konkretno, za c = 12 minimalni ukupni troškovi proizvodnje iznose 864 n.j. Ti se troškovi dobiju kao zbroj 32 · 3² + f₂(12 – 3), odnosno postižu se proizvodnjom točno \(x_3^*\) = 3 komada proizvoda u trećem mjesecu, te točno 12 – 3 = 9 proizvoda u prva dva mjeseca. Za c = 9 odgovarajuća optimalna količina proizvodnje u drugom mjesecu je \(x_2^*\) = 3, pa u drugom mjesecu treba proizvesti točno 3 proizvoda. Stoga u prvom mjesecu treba proizvesti točno \(x_1^*\) = 12 – (3 + 3) = 6 proizvoda.

Dakle, traženi optimalni plan proizvodnje je:

Mjesec	optimalan broj proizvoda
1.	6
2.	3
3.	3

Tablica 14. Rješenje Primjera 3

a pripadni optimalni troškovi proizvodnje iznose f₃(12) = 864 n.j.

Rješenje s pomoću programa WinQSB: U ovome ćemo primjeru postupiti analogno Primjeru 1, ali uz jednu nužnu modifikaciju. Naime, problem naprtnjače je maksimizacijski problem, tj. traži se maksimizacija vrijednosti svih namirnica koje stavljamo u naprtnjaču. Stoga potprogram DP pri rješavanju problema naprtnjače traži maksimum funkcije cilja. No problem koji ovdje promatramo je minimizacijski problem jer zahtijevamo minimizaciju ukupnih troškova. Na temelju standardne veze između problema minimizacije i problema maksimizacije:

min f(x) = –max(–f(x)),

gdje je f(x) funkcija cilja, polazni matematički model možemo zapisati u obliku:

maksimizirati f(x₁, x₂, x₃) = –10 × \(x_1^2\) – 24 × \(x_2^2\) – 32 × \(x_3^2\)

pod uvjetima

x₁ + x₂ + x₃ = 12,

\( x_1,x_2,x_3\in [6]_0 \).

Ovaj problem možemo riješiti potpuno analogno kao i zatvoreni problem naprtnjače, pri čemu modificiranu funkciju cilja npr. možemo shvatiti kao ukupne troškove prijevoza svih vrsta namirnica (svaki negativni predznak uobičajeno ekonomski interpretiramo kao trošak).

Pokrenimo potprogram DP, odaberimo proceduru Knapsack Problem, nazovimo problem koji ćemo rješavati Primjer 3 i, kao Number of Items ponovno upišimo 3. Potom kliknimo na OK.

U sljedećem koraku unesimo ulazne podatke.

U drugi stupac (Item Identification) upišimo M1, M2 i M3. Te oznake sugerirat će nam na koji se mjesec (prvi, drugi ili treći) odnosi odgovarajući rezultat.

U treći stupac (Units Available) upišimo najveće moguće kapacitete mjesečne proizvodnje. Sva tri kapaciteta su jednaka 6, pa u stupac unosimo tri ''šestice''.

U četvrti stupac (Unit Capacity Required), kako smo već istaknuli u rješenju Primjera 1, upisujemo tri ''jedinice''.

U peti stupac (Return Function (X: Item ID)) upisujemo pojedine komponente modificirane funkcije cilja, tj. funkcije cilja koja se odnosi na odgovarajući problem maksimizacije. Upisujemo redom: –10*X^2, -24*X^2 i -32*X^2.

U posljednji redak tablice (Capacity =) upišimo ukupnu količinu proizvoda koju treba proizvesti, tj. 12.

Time je unos ulaznih podataka završen. Kliknimo na izbornik Solve and Analyze, a potom na opciju Solve the Problem. Dobivamo tablicu u kojoj je navedeno optimalno rješenje promatranoga problema.

To optimalno rješenje očitavamo u trećem stupcu tablice (Decision Quantity). Iz tog stupca proizlazi da u prvom mjesecu treba proizvesti 6 proizvoda, a u drugom i trećem po 3 proizvoda. Ukupne minimalne troškove proizvodnje ''očitamo'' iz posljednjega retka (Total Return Value): ondje je naveden broj –864. Negativan predznak, kako smo istaknuli, označava da je riječ o troškovima, pa zaključujemo da su optimalni ukupni troškovi proizvodnje 864 n.j.

Primjer 4. Koristeći se programom WinQSB analizirajmo što bi se dogodilo s optimalnim rješenjima Primjera 3 kada bi najveći mjesečni kapacitet proizvodnje bio 6000 komada, a tromjesečna potražnja 12000 komada.[11].

Uzmemo li kao mjernu jedinicu 1000 komada proizvoda, dobit ćemo sljedeći optimalan plan:

mjesec

optimalna proizvodnja

[000 kom.]

Tablica 15. Prvi optimalan plan proizvodnje u Primjeru 4

pri čemu optimalni ukupni troškovi proizvodnje iznose 864 milijuna n.j. Taj se optimalni plan dobije izravno iz gore navedenoga rješenja Primjera 3 uz nužno redefiniranje odgovarajućih mjernih jedinica.

Uzmemo li kao mjernu jedinicu 100 komada proizvoda, tj. da su mjesečni kapacitet proizvodnje 60 [stotina komada proizvoda] i planirana tromjesečna potražnja 120 [stotina komada proizvoda], dobit ćemo sljedeći optimalan plan:

mjesec

optimalna proizvodnja

[stotina kom.]

Tablica 16. Drugi optimalan plan proizvodnje u Primjeru 4

pri čemu optimalni ukupni troškovi proizvodnje iznose 853 760 000 n.j. Dobiveni optimalni plan očito se bitno razlikuje od plana navedenog u tablici 15.

Nadalje, uzmemo li kao mjernu jedinicu 10 komada proizvoda, tj. da su mjesečni kapacitet proizvodnje 600 [desetina komada proizvoda] i planirana tromjesečna potražnja 1200 [desetina komada proizvoda], dobit ćemo sljedeći optimalan plan:

mjesec

optimalna proizvodnja

[desetina kom.]

600

343

257

Tablica 17. Treći optimalan plan proizvodnje u Primjeru 4

pri čemu pripadni optimalni troškovi proizvodnje iznose 853 714 400 n.j. Isti rezultat dobiva se ako se za mjernu jedinicu uzme 5 komada proizvoda. Izborom 1 komada proizvoda za mjernu jedinicu dobiva se poruka programa Subscript out of range, tj. nemogućnost rješavanja problema. Stoga možemo zaključiti da je optimalno rješenje \[(x_1^*,x_2^*,x_3^*) = (6000,3430,2570)\] i da je u ovom slučaju za mjernu jedinicu proizvodnje pogodno odabrati 10 komada proizvoda, a ne 1000 komada proizvoda, kako se isprva čini.

Primjer 5. Tijekom jednoga mjeseca (4 tjedna) treba proizvesti točno 11 komada nekoga proizvoda. Troškovi proizvodnje x_i komada proizvoda u i–tom tjednu zadani su izrazom w_i ×\(x_i^2\), gdje su w_i strogo pozitivni realni parametri. Tijekom jednoga tjedna moguće je proizvesti najviše 5 komada proizvoda (moguće je da u jednom tjednu ne bude proizveden niti jedan proizvod). Treba izraditi plan proizvodnje tako da ukupni troškovi budu minimalni.

a) Odredimo matematički model promatranoga problema.

b) Riješimo model za w₁ = 12, w₂ = 24, w₃ = 40 i w₄ = 30.

Matematički model: Ukupne troškove proizvodnje računamo prema formuli

f (x₁, x₂, x₃, x₄) =\(\sum\limits_{i = 1}^4 {{w_i} \cdot x_i^2} \).

Ukupan broj proizvedenih komada mora biti jednak 11, što znači da mora vrijediti jednakost

\( \sum\limits_{i = 1}^4 {{x_i}} = 11\).

Budući da se tijekom jednoga tjedna može proizvesti najviše 5 komada proizvoda i da ukupan broj proizvedenih komada nužno mora biti prirodan broj ili nula, za svaki \(i \in [4]\) vrijedi uvjet \(x_i \in [5]_0\). Stoga odgovarajući matematički model glasi:

minimizirati f (x₁, x₂, x₃, x₄) = \(\sum\limits_{i = 1}^4 {{w_i} \cdot x_i^2} \)

pod uvjetima

\(\sum\limits_{i = 1}^4 {{x_i}} = 11\);

\(x_i\in [5]_0\), za svaki \(i \in [4]\).

b) U konkretnom je slučaju matematički model sljedeći:

minimizirati f (x₁, x₂, x₃, x₄) = \(12 \cdot x_1^2 + 24 \cdot x_2^2 + 40 \cdot x_3^2 + 30 \cdot x_4^2\)

pod uvjetima

\(\sum\limits_{i = 1}^4 {{x_i}} = 11\);

\(x_i\in [5]_0\), za svaki \(i \in [4]\).

Analitičko rješenje: Stavimo C := [11]₀, pa za svaki \(c\in C\) računamo vrijednosti četiriju realnih funkcija \(f_1,f_2,f_3,f_4:C\to \mathbb{R}\):[12]

f₁(c) = 12 × c²;

f₂(c) =\( \min\limits_{\begin{subarray}{l} 0 \leqslant {x_2} \leqslant \min \left\{ {c,5} \right\} \\ {x_2} \in \mathbb{Z} \end{subarray}} \left[ {24 \cdot x_2^2 + {f_1}(c - {x_2})} \right]\);

f₃(c) =\( \min\limits_{\begin{subarray}{l} 0 \leqslant {x_3} \leqslant \min \left\{ {c,5} \right\} \\ {x_3} \in \mathbb{Z} \end{subarray}} \left[ {40 \cdot x_3^2 + {f_2}(c - {x_3})} \right]\);

f₄(c) =\( \min\limits_{\begin{subarray}{l} 0 \leqslant {x_4} \leqslant \min \left\{ {c,5} \right\} \\ {x_4} \in \mathbb{Z} \end{subarray}} \left[ {30 \cdot x_4^2 + {f_3}(c - {x_4})} \right]\).

Pri izračunu vrijednosti ovih funkcija treba imati na umu da zbog polaznih uvjeta ne postoje sljedeće vrijednosti:

\(f_1(6),f_1(7),\ldots,f_1(11) \) jer se u prvom (ali i bilo kojem!) tjednu može proizvesti najviše 5 proizvoda;
f₂(11) jer se u prva (ali i bilo koja!) dva tjedna može proizvesti najviše 2 × 5 = 10 proizvoda.

Izračunom svih vrijednosti definiranih realnih funkcija dobiva se sljedeća tablica:

c	\(f_1(c)\)	\(x_1^*\)	f₂(c)	\(x_2^*\)	f₃(c)	\(x_3^*\)	f₄(c)	\(x_1^*\)
0	0	0	0	0	0	0	0	0
1	12	1	12	0	12	0	12	0
2	48	2	36	1	36	0	36	0
3	108	3	72	1	72	0	66	1
4	192	4	132	1	112	1	102	1
5	300	5	204	2	172	1	142	1
6	\(\infty\)	5	288	2	244	1	202	1
7	\(\infty\)	5	396	2	328	1	274	1
8	\(\infty\)	5	516	3	436	1	358	1
9	\(\infty\)	5	684	4	556	1, 2	448	2
10	\(\infty\)	5	900	5	676	2	556	2
11	\(\infty\)	5	\(\infty\)	5	844	2	676	2

Tablica 18. Rezultati svih četiriju faza rješenja Primjera 5

(Zapis 1, 2 označava da se optimalna vrijednost odgovarajuće funkcije postiže za \(x_3^*\) = 1 i za \(x_3^*\) = 2).

Preostaje ''očitati'' rješenje postavljenoga problema. Optimalna vrijednost ukupnih troškova proizvodnje 11 komada proizvoda jednaka je f₄(11) = 676 n.j. Ta se vrijednost postiže za \(x_4^*\) = 2, što znači da u četvrtom tjednu treba proizvesti točno dva proizvoda. Stoga u prva tri tjedna treba proizvesti ukupno 11 – 2 = 9 proizvoda. Optimalni troškovi proizvodnje točno 9 proizvoda u prva tri tjedna iznose f₃(9) = 556 n.j. i postižu se za \(x_3^*\) = 1 ili \(x_3^*\) = 2. Zbog toga razlikujemo dvije mogućnosti:

1) U trećem tjednu proizvede se točno jedan proizvod (tj. \(x_3^*\) = 1). Tada u prva dva tjedna treba proizvesti točno 9 – 1 = 8 proizvoda. Optimalni troškovi proizvodnje 8 proizvoda u prva dva tjedna iznose f₂(8) = 516 n.j. i postižu se za \(x_3^*\) = 3. Zbog toga u drugom tjednu treba proizvesti točno 3 proizvoda, pa u prvom tjednu preostaje proizvesti ukupno \(x_1^*\) = 8 – 3 = 5 proizvoda.

2) U trećem tjednu proizvedu se točno dva proizvoda (tj. \(x_3^*\)= 2). Tada u prva dva tjedna treba proizvesti točno 9 – 2 = 7 proizvoda. Optimalni troškovi proizvodnje 7 proizvoda u prva dva tjedna iznose f₂(7) = 396 n.j. i postižu se za \(x_2^*\) = 2. Stoga u drugom tjednu treba proizvesti točno 2 proizvoda, pa u prvom tjednu preostaje proizvesti točno \(x_1^*\) = 7 – 2 = 5 proizvoda.

Tako smo dobili ukupno dva optimalna plana proizvodnje:

Plan 1:

tjedan

optimalna proizvodnja

[kom.]

Tablica 19. Prvi optimalan plan proizvodnje u Primjeru 5

Plan 2:

tjedan

optimalna proizvodnja

[kom.]

Tablica 20. Drugi optimalan plan proizvodnje u Primjeru 5

Rješenje s pomoću programa WinQSB: Na ovom ćemo primjeru uočiti jedan od glavnih nedostataka potprograma DP: nemogućnost ispisa barem dvaju optimalnih rješenja (ako ona postoje, naravno). Naime, potprogram će – kao izlazni rezultat – ispisati točno jedan optimalni plan i ne postoji nikakva mogućnost da bilo kojom od implementiranih procedura dobijemo ispis drugoga optimalnog plana.

Sâm postupak rješavanja problema s pomoću programa WinQSB potpuno je analogan onome iz prethodnoga primjera. Najprije problem minimizacije ''pretvorimo'' u problem maksimizacije:

maksimizirati f (x₁, x₂, x₃, x₄) = \( - 12 \cdot x_1^2 - 24 \cdot x_2^2 - 40 \cdot x_3^2 - 30 \cdot x_4^2\)

pod uvjetima

x₁ + x₂ + x₃ + x₄ = 11;

\( x_1,x_2,x_3,x_4 \in [5]_0 \).

Potom pokrenemo potprogram DP, odaberemo proceduru Knapsack Problem, nazovimo problem koji ćemo rješavati Primjer 5, a u pravokutnik pored natpisa Number of Items upišimo 4. Potom kliknimo na OK.

Unesimo ulazne podatke za razmatrani primjer na sljedeći način:

u drugi stupac (Item Identification) upišimo: T1, T2, T3 i T4. Tako ćemo u izlaznom rezultatu moći ''očitati'' opseg proizvodnje u svakom pojedinom tjednu;
u treći stupac (Units Available) upišimo maksimalne tjedne kapacitete proizvodnje: oni su jednaki 5, pa upišimo ukupno četiri ''petice'';
u četvrti stupac (Unit Capacity Required) upišimo onoliko ''jedinica'' koliko imamo tjedana: dakle, upišimo četiri ''jedinice'';
u peti stupac (Return Function (X: Item ID)) upišimo komponente modificirane funkcije cilja koje se odnose na svaki pojedini tjedan: dakle, upišimo redom –12*X^2, –24*X^2, –40*X^2 i –30*X^2;
u posljednji redak (Capacity=) upišimo ukupan broj komada proizvoda koje treba proizvesti, tj. 11.

Ovime je unos ulaznih podataka završen. Lijevom tipkom miša kliknimo na izbornik Solve and Analyze i odaberimo opciju Solve the Problem. Kao rješenje razmatranoga problema dobivamo samo Plan 2 iz analitičkoga rješenja, tj. u prvom tjednu treba proizvesti 5 komada proizvoda, a u svakom od preostala tri tjedna po dva komada proizvoda. Vrijednost Total Return Value = –676 znači da pripadni optimalni ukupni troškovi iznose 676 n.j.

Primjer 6. Analogno u Primjeru 4, koristeći se računalnim programom WinQSB, analizirajmo što bi se dogodilo s optimalnim rješenjima kada bi najveći tjedni kapacitet proizvodnje bio 5000 komada, a mjesečna potražnja 11000 komada proizvoda.[13]

Uzmemo li kao mjernu jedinicu 1000 komada, dobit ćemo sljedeći optimalan plan:

Plan 1*:

tjedan

optimalna proizvodnja

[000 kom.]

Tablica 21. Prvi optimalan plan proizvodnje u Primjeru 6

uz pripadne optimalne troškove od 676 milijuna kuna. Primijetimo da je i plan

Plan 2*:

tjedan

optimalna proizvodnja

[000 kom.]

Tablica 22. Drugi optimalan plan proizvodnje u Primjeru 6

također optimalan. Oba navedena plana mogu se dobiti izravno iz analitičkoga rješenja Primjera 5 uz odgovarajuće redefiniranje mjernih jedinica, a drugi navedeni plan (ponovno) nije moguće dobiti s pomoću programa WinQSB.

Uzmemo li kao mjernu jedinicu 100 komada proizvoda, dobit ćemo sljedeći optimalan plan:

Plan 1**:

tjedan	1.	2.	3.	4.
optimalna proizvodnja [stotina kom.]	50	25	15	20

Tablica 23. Treći optimalan plan proizvodnje u Primjeru 6

Dakle, u prvom tjednu treba proizvesti 5000 komada proizvoda, u drugom 2500 komada proizvoda, u trećem 1500 komada proizvoda, a u četvrtom 2000 komada proizvoda uz pripadne optimalne troškove od 660 milijuna n.j. Isti rezultat dobije se ako se kao mjerne jedinice odaberu 10 komada proizvoda, odnosno 5 komada proizvoda. Stoga je u ovom slučaju za mjernu jedinicu proizvodnje pogodno odabrati 100 komada proizvoda.

Zanimljivo je primijetiti da je Plan 1**, grubo govoreći, aritmetička sredina Planova 1* i 2*. Preciznije, optimalna proizvodnja u i–tom tjednu prema Planu 1** je aritmetička sredina optimalnih planova proizvodnje u istom tjednu dobivenih prema Planu 1* i Planu 2*.

Zaključno istaknimo da postoje još neki ekonomski problemi koji se mogu svesti na problem jednostavne razdiobe ulaganja, ali ih zbog opsežnosti članka ovdje nismo razmatrali. Čitatelje zainteresirane za daljnje primjene upućujemo na literaturu [1] ili [5].

LITERATURA:

1. M.J. Beckmann: Dynamic Programming of Economic Decisions, Springer–Verlag, New York, 1968

2. R. Bellman: Dynamic Programming, Dover Publications, 2003

3. D. Kalpić, V. Mornar: Operacijska istraživanja, ZEUS, Zagreb, 1996.

4. L. Neralić: Uvod u matematičko programiranje 1, Element, Zagreb, 2003.

5. J. Petrić: Operaciona istraživanja, Nauka, Beograd, 1997.

6. J. Petrić et.al.: Operaciona istraživanja – zbirka rešenih zadataka, Nauka, Beograd, 1996.

7. H. Kellerer, U. Pferschy, D. Pisinger: Knapsack Problems, Springer, 2004

8. S. Martello, P. Toth: Knapsack Problems, Wiley, 1990

[1] S web-stranice http://www.wiley.com/college/tech/winqsb.htm može se ''skinuti'' besplatna verzija programa WinQSB.

[2] Iz navedenih razloga u takvim slučajevima govorimo o cjelobrojnom programiranju.

[3] Navedeno svojstvo programa WinQSB je, zapravo, njegova osnovna manjkavost jer smo, prigodom rješavanja problema u kojima je relativna većina svih numeričkih vrijednosti strogo veća od 500, zapravo prisiljeni na redefiniranje pripadnih mjernih jedinica.

[4] Skraćenica za: novčanih jedinica. U danom primjeru, taj iznos može biti višekratnik nekog elementa iz skupa {1, 100, 1.000, 1.000.000 ... }.

[5] Vrijednost predmeta obično se definira kao umnožak njegove mase (ili obujma) i jedinične cijene (tj. cijene po jedinici mase ili obujma).

[6] Vrijednost namirnice obično se definira kao umnožak njezine mase (ili obujma) i jedinične cijene (tj. cijene po jedinici mase ili obujma).

[7] Pritom pretpostavljamo da su sve vrijednosti M, v_i i m_i nenegativne (to su tzv. prirodni uvjeti).

[8] Izomorfni modeli se, dakle, mogu razlikovati u interpretacijama, ali ne i u tipovima varijabli. Npr. ako su u modelu A varijable nužno cjelobrojne, a u modelu B nužno realne, onda takvi modeli nisu izomorfni. Analogna tvrdnja vrijedi i za (ne)jednadžbe koje opisuju uvjete.

[9] Označimo li sa S skup svih mogućih iznosa ulaganja, onda je za svaki \( i \in [n]\) \(f_i:S\to \mathbb{R}\) realna funkcija čije su vrijednosti u konkretnom slučaju zadane tablično, a ne analitički (formulom). Zbog toga ovaj primjer ne rješavamo koristeći se računalnim programom WinQSB.

[10] C = 4 posljedica je zahtjeva da svi iznosi ulaganja moraju biti višekratnici broja 1.000.000. Bez toga zahtjeva, tj. samo uz zahtjev cjelobrojnosti ulaganja, morali bismo uzeti C = 4.000.000. Radi jednostavnosti i računanja s ''manjim brojevima'', valutna jedinica kapitala u ovome je slučaju 1.000.000,00 kn.

[11] Svi ostali numerički podaci ostaju neizmijenjeni.

[12] Preciznije, problem se rješava u ukupno četiri faze, pri čemu se, za svaki \( i\in [4] \), u i–toj fazi računaju vrijednosti funkcije f_i.

[13] Svi ostali numerički podaci ponovno ostaju neizmijenjeni.

Kvantitativne metode odlučivanja – problem optimalne zamjene opreme

mr. sc. Bojan Kovačić, dipl. ing. matematike,
RRiF – Visoka škola za financijski menadžment,
10 000 Zagreb,
Martićeva 29,
e-mail: bojan.kovacic@rrif.hr

Problem optimalne zamjene opreme jedan je od osnovnih problema u cjelokupnoj industriji. Sastoji se u određivanju optimalnoga trenutka zamjene stare opreme novom pod uvjetima da se opseg proizvodnje poveća, a troškovi proizvodnje umanje, tako da se time potpuno nadoknade troškovi kupnje nove opreme, gubici uzrokovani zastojem u proizvodnji zbog uvođenja nove opreme i troškovi obuke djelatnika za rad na novoj opremi.

Temeljni zadatak je odrediti optimalnu politiku modernizacije i zamjene opreme prihvaćajući pritom različite uvjete vezane za tekuće održavanje, karakteristike proizvodnje i predviđeni tehnološki razvoj. Ovakav proces očito zahtijeva analizu u više faza, pa se time dinamičko programiranje nameće kao prikladan način rješavanja ovakvih problema.

Neki tipovi problema zamjene opreme i načini njihova rješavanja ilustriraju se na sljedećim primjerima. U rješenjima pojedinih primjera koriste se računalni programi Graph Magics i Grin čije su besplatne probne (trial) verzije dostupne za preuzimanje putem Interneta.

Primjer 1

Utvrđena poslovna politika neke tvrtke predviđa korištenje automobila u sljedećih n = 5 godina, pa je na početku prve godine razdoblja planiranja kupljen novi automobil po nabavnoj cijeni od p = 12 n.j.1 Radi jednostavnosti, pretpostavlja se da je nabavna cijena automobila stalna tijekom cijeloga razdoblja planiranja te da će po isteku razdoblja planiranja automobil obavezno biti rashodovan. Godišnji neto troškovi održavanja automobila (c_{i}) i likvidacijska vrijednost2 automobila (s_{i}) iskazani su kao funkcija starosti automobila:

starost automobila (i) [god.]	0	1	2	3	4	5
godišnji neto trošak održavanja (c_{i}) [n.j.]	2	4	5	9	12	12
likvidacijska vrijednost (s_{i}) [n.j.]	-	7	6	2	1	0

Niz (c_{i})_{i \in \mathbb{N}} nužno je rastući, tj. povećanjem starosti automobila povećavaju se i godišnji troškovi njegova održavanja. Zbog tog razloga nakon određenog vremena može biti ekonomski isplativije rashodovati do tada korišteni automobil i kupiti novi. S druge je strane niz (s_{i})_{i \in \mathbb{N}} nužno padajući, tj. povećanjem starosti automobila smanjuje se njegova likvidacijska vrijednost.

Politika zamjene u ovome je slučaju donošenje odluke treba li zadržati postojeći automobil ili ga rashodovati i kupiti novi automobil. Navedeno odlučivanje na dnevni red dolazi početkom svake pojedine godine. Najjednostavniji primjeri politika zamjene su:

P_{1}) zamjena automobila, tj. rashodovanje do tada korištenoga automobila i kupnja novoga početkom svake pojedine godine (tj. početkom druge, treće, četvrte i pete godine);

P_{2}) zadržavanje postojećeg automobila sve do kraja pete godine.

U razmatranom je primjeru početkom prve godine već donesena odluka o kupnji novog automobila. Stoga se odluke donose početkom svake od sljedeće četiri godine. Budući da je početkom svake od tih godina moguće donijeti točno dvije različite odluke, postoji ukupno 16 međusobno različitih politika zamjene. Stoga je od interesa odrediti najbolju među njima, tj. odrediti optimalnu politiku zamjene.

Optimalna politika zamjene je politika zamjene koja osigurava najmanje ukupne neto troškove uporabe automobila tijekom svih pet godina. U promatranom primjeru to znači ispitati svih 16 međusobno različitih politika zamjene i među njima odrediti najbolju. No, takva je metoda za iole veće vrijednosti n općenito vrlo spora i neučinkovita, pa se stoga nameće problem iznalaženja dovoljno učinkovitih metoda i algoritama za određivanje optimalne politike. U tu se svrhu primjenjuju metode i tehnike dinamičkoga programiranja.

Primjer 1 može se riješiti «klasično», tj. definiranjem odgovarajućih rekurzivnih relacija, ali ovdje će biti riješen svođenjem na problem najkraćega puta u grafu. Matematički model koji će se koristiti je potpuni težinski digraf. Vrhovi toga digrafa predstavljat će početke godina, tj. vrh i označavat će početak godine i. Budući da se korištenje automobila planira u sljedećih n = 5 godina, graf će imati ukupno n + 1 = 6 vrhova: 1, 2, 3, 4, 5 i 6. Nadalje, za svaki uređeni par (i, j) takav da je i \lt j vrhovi i i j bit će spojeni usmjerenim bridom (lukom) čiji je početak u vrhu i, a kraj u vrhu j. Ukupan broj međusobno različitih lukova u tako dobivenom modelu jednak je

\binom{n+1}{2}=\binom{6}{2} = 15 \text{.}

Preostaje definirati težinu svakog od dobivenih lukova. Budući da treba minimizirati ukupne neto troškove, težina w_{ij} luka (i, j) definira se kao:

\begin{split} w_{ij}&= (\text{nabavna cijena automobila na početku godine } i)\\ &\quad + (\text{troškovi održavanja u godinama } i, i + 1, \ldots, j - 1) \\ &\quad - (\text{likvidacijska vrijednost automobila na početku godine } j). \end{split}

Odatle slijedi da je analitički izraz za izračunavanje težina w_{ij}:

w_{ij} = p_{i} + c_{0} + c_{1} + \ldots + c_{j-1-i}-s_{j-i} = p_{i} + \sum_{k=0}^{j-i-1}c_{k} - s_{j-i}.

Ovdje prešutno pretpostavljamo da se kraj godine k podudara s početkom godine (k + 1).

U razmatranom se primjeru pretpostavlja da je nabavna cijena automobila na početku svake godine ista i jednaka 12 n.j., tj. vrijedi jednakost p_{1} = p_{2} = p_{3} = p_{4} = p_{5} = p = 12. Zbog toga vrijedi i jednakost:

w_{ij} = w_{i+k,j+k} ,

za sve i,j,k za koje su definirane obje strane jednakosti. Tako se dobiva:

\begin{align*} w_{12}& = w_{23} = w_{34} = w_{45} = w_{56} = p + c_{0} - s_{1} = 12+2-7 = 7 ; \\ w_{13}& = w_{24} = w_{35} = w_{46} = p + (c_{0} + c_{1}) - s_{2} = 12+2+4-6 = 12 ; \\ w_{14}& = w_{25} = w_{36} = p + (c_{0} + c_{1} + c_{2}) - s_{3} = 12+2+4+5-2 = 21 ; \\ w_{15}& = w_{26} = p + (c_{0} + c_{1} + c_{2} + c_{3}) - s_{4} = 12+2+4+5+9-1 = 31 ; \\ w_{16}& = p + (c_{0} + c_{1} + c_{2} + c_{3} + c_{4}) - s_{5} = 12+2+4+5+9+12-0 = 44 \text{.} \end{align*}

Za rješavanje primjera u nastavku koristimo se računalnim programom Graph Magics. Koristeći se njime, modeliramo navedeni problem potpunim težinskim digrafom, koji je prikazan na slici 1.

Slika 1: Model problema iz primjera 1.

Radi određivanja najkraćega puta, vrh 1 označi se kao početni vrh, a vrh 6 kao završni vrh. Koristeći se procedurom Find Shortest Path (from Start Vertex to End) određuje se najkraći put između vrhova 1 i 6:

1 — 2 — 4 — 6.

Njegova je težina jednaka 31. Unutrašnji vrhovi dobivenoga najkraćeg puta su 2 i 4, što znači da početkom tih godina treba rashodovati dotad korišteni automobil i zamijeniti ga novim. Prema tome, optimalna politika zamjene glasi:

\bullet	početak 2. godine: rashodovanje dotad korištenog automobila i kupnja novoga;
\bullet	početak 3. godine: zadržavanje dotad korištenog automobila;
\bullet	početak 4. godine: rashodovanje dotad korištenog automobila i kupnja novoga;
\bullet	početak 5. godine: zadržavanje dotad korištenog automobila;
\bullet	kraj 5. godine/početak 6. godine: rashodovanje dotad korištenog automobila.

Rješavanje «klasičnim» putem daje još jedan najkraći put:

1 — 3 — 5 — 6.

U ovom slučaju na početku treće i na početku pete godine razdoblja planiranja treba rashodovati dotad korišteni automobil i zamijeniti ga novim, tj. optimalna politika zamjene glasi:

\bullet	početak 2. godine: zadržavanje dotad korištenog automobila;
\bullet	početak 3. godine: rashodovanje dotad korištenog automobila i kupnja novoga;
\bullet	početak 4. godine: zadržavanje dotad korištenog automobila;
\bullet	početak 5. godine: rashodovanje dotad korištenog automobila i kupnja novoga;
\bullet	kraj 5. godine/početak 6. godine: rashodovanje dotad korištenog automobila.

Obje navedene optimalne politike postižu najmanji iznos ukupnih neto troškova 31 n.j.

Primjer 2

Usporedno s redovnim studiranjem Ivan je putem Student–servisa dobio honorarni posao dostavljača lokalnih besplatnih novina, oglasnoga materijala itd. Za taj mu je posao potreban bicikl koji trenutačno ne posjeduje. Trenutačna cijena novoga bicikla je p = 500 n.j. Novi bicikl može se koristiti najviše 3 godine, a potom ga treba prodati. Godišnji neto trošak održavanja bicikla i likvidacijska vrijednost bicikla, iskazani kao funkcije starosti bicikla, navedeni su u sljedećoj tablici:

starost bicikla (i) [god.]	0	1	2	3
godišnji neto trošak (c_{i}) [n.j.]	30	40	60	-
likvidacijska vrijednost (s_{i}) [n.j.]	-	400	300	250

Ako Ivan namjerava završiti svoj studij za točno 5 godina i dotad honorarno raditi kao dostavljač, treba odrediti optimalnu politiku zamjene bicikla tijekom razdoblja od 5 godina (pretpostavlja se da je cijena novoga bicikla stalna u cjelokupnom razdoblju planiranja te da će Ivan na kraju razdoblja planiranja obavezno prodati bicikl).

Prije rješavanja zadatka korisno je napraviti jednostavnu analizu kojom se pokušava utvrditi koje je «trajanje vlasništva» najekonomičnije, tj. je li općenito bolje zadržati bicikl 1, 2 ili 3 godine?

Kupi li Ivan bicikl, bude li ga koristio jednu godinu i potom ga prodao, prosječan (zapravo ukupan) godišnji neto trošak iznosit će p + c_{0} - s_{1} = 500 + 30 - 400 = 130 n.j.

Kupi li Ivan bicikl, bude li ga koristio ukupno dvije godine i potom ga prodao, prosječan godišnji neto trošak iznosit će

\frac{p + (c_{0} + c_{1}) - s_{2}}{2} = \frac{500 + (30 + 40) - 300}{2} = 135 \text{ n.j.}

Ako Ivan kupi bicikl, bude li ga koristio sve tri godine i potom ga prodao, prosječan godišnji neto trošak iznosit će

\frac{p + (c_{0} + c_{1} + c_{2}) - s_{3}}{3} = \frac{500 + (30 + 40 + 60) - 250}{3} = 126.67 \text{ n.j.}

Ova analiza pokazuje da je najisplativije zadržati bicikl sve tri godine i potom ga prodati, a ako to nije moguće, onda je najisplativije zadržati bicikl točno jednu godinu. Budući da je razdoblje planiranja n = 5 godina, može se procijeniti da će optimalna politika zamjene biti «kombinacija» jednogodišnjeg i trogodišnjeg trajanja vlasništva.

I u ovom se slučaju problem modelira težinskim digrafom, ali taj digraf neće biti potpun. Naime, bicikl se može koristiti najviše tri godine, a to je razdoblje strogo manje od razdoblja planiranja. Stoga neki vrhovi digrafa neće biti spojeni niti jednom spojnicom. Vrhovi digrafa ponovo će označavati početke godina, pa će graf imati ukupno n + 1 = 6 vrhova. Vrh i označavat će početak godine i (pritom se pretpostavlja da se kraj pete godine podudara s početkom šeste godine). Budući da se bicikl može koristiti najviše 3 godine, luk (i, j) postoji ako i samo ako vrijedi nejednakost 0 \lt j - i \leq 3. Stoga je skup svih lukova grafa jednak E = \lbrace (1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5)\rbrace. Težine pojedinih lukova izračunavaju se kao u primjeru 1:

\begin{align*} w_{12}& = w_{23} = w_{34} = w_{45} = w_{56} = p + c_{0} - s_{1} = 500+30-400 = 130 ; \\ w_{13}& = w_{24} = w_{35} = w_{46} = p + (c_{0} + c_{1}) - s_{2} = 500+(30+40)-300 = 270 ; \\ w_{14}& = w_{25} = w_{36} = p + (c_{0} + c_{1} + c_{2}) - s_{3} = 500+(30+40+60)-250 = 380 \text{.} \end{align*}

Težinski digraf dobiven uz pomoć programa Graph Magics prikazan je na slici 2.

Slika 2: Model problema iz primjera 2.

Najkraći put između vrhova 1 i 6 je

1 — 2 — 3 — 6,

čija je težina 640. Prema tome, optimalna politika zamjene bicikla je sljedeća:

\bullet	početak 2. godine: prodaja dotad korištenoga bicikla i kupnja novoga bicikla;
\bullet	početak 3. godine: prodaja dotad korištenoga bicikla i kupnja novoga bicikla;
\bullet	početak 4. godine: zadržavanje dotad korištenoga bicikla;
\bullet	početak 5. godine: zadržavanje dotad korištenoga bicikla;
\bullet	kraj 5. godine/početak 6. godine: prodaja dotad korištenoga bicikla.

Dobivena optimalna politika uistinu je kombinacija trajanja vlasništva od jedne, odnosno tri godine, tj. navedenoj optimalnoj politici odgovara rastav 5 = 1 + 1 + 3. Vrijedi istaknuti da je ukupan broj različitih optimalnih politika jednak ukupnom broju različitih načina na koji se broj 5 može napisati kao zbroj barem jedne «jedinice» i barem jedne «trojke», a taj je jednak 3. Ti načini su: 1 + 1 + 3, 1 + 3 + 1, 3 + 1 + 1 i svaki od njih generira jednu optimalnu politiku (prvi način generira gore navedenu optimalnu politiku, drugi način generira optimalnu politiku kupnje novoga bicikla u 2. i 5. godini, a treći optimalnu politiku kupnje novoga bicikla u 4. i 5. godini). Sve tri optimalne politike daju iste minimalne ukupne neto troškove u iznosu od 640 n.j.

U prethodnim primjerima razmatrani su slučajevi u kojima je na početku prve godine već bila donesena odluka o kupnji nove opreme (automobila, bicikla), pa su se sve ostale odluke donosile na početku svake od sljedećih n godina (tu uključujemo i završnu odluku o rashodovanju opreme). Međutim, u praksi se nerijetko javljaju slučajevi u kojima na početku prve godine već raspolažemo s opremom starom i godina, čiji je vijek trajanja ukupno n godina, pa treba razmotriti optimalnu politiku zamjene u sljedećih n - i godina. I u takvim se slučajevima problem zamjene opreme može svesti na problem najkraćega puta u digrafu, no, u takvom se grafu pojavljuju negativne težine lukova i višestruki lukovi između dvaju vrhova, pa navedeni problem nije moguće riješiti uz pomoć računalnoga programa Graph Magics. Stoga će se takav problem riješiti «klasično» ilustrirajući tehniku dinamičkoga programiranja koja se ovdje primjenjuje.

Primjer 3

Pretpostavlja se da se na početku prve godine raspolaže vozilom starim dvije godine. Vozilo je potrebno koristiti u sljedeće n = 3 godine, pri čemu se na početku svake godine (uračunavajući i prvu!) donosi odluka: zadržati postojeće vozilo još godinu dana ili rashodovati postojeće vozilo i kupiti novo. Kao i prije, godišnji trošak održavanja vozila zadan je tablično kao funkcija starosti automobila:

starost automobila (i) [god.]	0	1	2	3	4
godišnji neto trošak (c_{i}) [n.j.]	10	20	40	60	70

Nadalje, cijena novoga vozila u sve je tri godine stalna i iznosi p = 60 n.j. Likvidacijska neto vrijednost automobila starog i godina zadana je funkcijom:

s_{i} = s(i) = 25 - 5 \cdot i \text{, za } i=1,2,3,4,5 \text{.}

Treba odrediti optimalnu politiku zamjene automobila u cjelokupnom razdoblju planiranja. Ukupan broj različitih politika zamjene jednak je 2^{n} = 2^{3} = 8 jer početkom svake godine donosimo jednu od dviju mogućih odluka.

Prvi korak u rješavanju problema je definiranje funkcije optimalne vrijednosti V=V(k,i) s:

\begin{align*} V(k,i) = \ & \text{najmanji ukupni neto troškovi od početka godine }k\text{ do kraja} \\ & \text{razdoblja planiranja (tj. početka godine }n + 1\text{) ako na početku} \\ & \text{godine }k\text{ raspolažemo vozilom starosti }i\text{.} \end{align*}

Funkcija V je funkcija dviju cjelobrojnih (točnije, prirodnih) varijabli: k i i. Varijabla k naziva se varijabla etape i ona «mjeri» razdoblja (etape) u kojima se donosi točno jedna odluka. U ovom slučaju varijabla etape poprima vrijednosti iz skupa \lbrace 1, 2, 3, 4\rbrace jer će se početkom 1., 2., 3. i 4. godine donositi odluka o zadržavanju ili rashodovanju vozila. Treba primijetiti da će početkom (n + 1)–te, tj. 4. godine biti donesena odluka o rashodovanju vozila jer će završiti planirano razdoblje u kojemu se želi koristiti vozilo. Varijabla i naziva se varijabla stanja i ona «mjeri» starost vozila na početku godine k. Ta će varijabla poprimati vrijednosti iz skupa \lbrace 1, 2, 3, 4, 5\rbrace jer najveća moguća starost vozila iznosi i_{\max} = 2 + 3 = 5 godina3.

Iz postavke navedenoga primjera slijedi da treba izračunati vrijednost V(1, 2) jer se na početku prve godine (k = 1) raspolaže vozilom starosti i = 2 godine. Navedena se vrijednost izračunava tako da se najprije definira dvoindeksna rekurzivna relacija koju zadovoljavaju vrijednosti V(k, i), a potom početni uvjeti koji omogućuju računanje konkretnih vrijednosti te funkcije.

Spomenuta dvoindeksna rekurzivna relacija dobiva se na sljedeći način: Pretpostavimo da se na početku godine k koristi vozilo staro i godina. Moguće su točno dvije alternative: A_{1}= zadržati vozilo još godinu dana i A_{2}= rashodovati vozilo i zamijeniti ga novim vozilom.

Ako se donese odluka A_{1}, tj. odluči li se zadržati vozilo i koristiti se njime u cijeloj godini k (do početka godine k + 1), ukupni neto trošak u godini k koji proizlazi iz takve odluke tvori isključivo neto trošak održavanja automobila starog i godina. Taj je trošak jednak c_{i}. Sljedeća etapa u kojoj se donosi odluka je početak (k + 1) godine, a u tom trenutku na raspolaganju će biti vozilo starosti i + 1 godina. Najmanji ukupni neto troškovi od početka (k + 1) godine do kraja razdoblja planiranja, prema definiciji funkcije V, iznose V(k + 1, i + 1). Prema tome, ukupni neto troškovi nastali kao posljedica izbora alternative A_{1} na početku godine k iznose c_{i} + V(k + 1, i + 1).

Ako se donese odluka A_{2}, tj. odluči li se rashodovati dotad korišteno vozilo i kupiti novo, u godini k pojavljuju se trošak nabave novoga vozila, godišnji trošak njegova održavanja te prihod dobiven rashodovanjem i prodajom dotadašnjega vozila, tj. prihod jednak likvidacijskoj vrijednosti dotadašnjega vozila. Trošak nabave novoga vozila jednak je njegovoj nabavnoj cijeni, tj. p. Godišnji neto trošak održavanja novoga vozila iznosi c_{0}, a likvidacijska vrijednost dotadašnjega vozila (staroga i godina) iznosi s_{i}. Stoga ukupni neto troškovi u godini k iznose p + c_{0} - s_{i}. Sljedeća etapa u kojoj se donosi odluka je početak (k + 1) godine, a u tom trenutku na raspolaganju je vozilo staro jednu godinu. Najmanji ukupni neto troškovi od početka (k + 1) godine do kraja razdoblja planiranja, prema definiciji funkcije V, iznose V(k + 1, 1). Prema tome, ukupni neto troškovi nastali kao posljedica izbora alternative A_{2} na početku godine k iznose p + c_{0} - s_{i} + V(k + 1, 1).

Budući da ukupne neto troškove treba minimizirati u svakoj pojedinoj etapi, iz navedenih razmatranja proizlazi sljedeća jednakost:

V(k, i) = \min \Big\lbrace c_{i} + V(k + 1, i + 1), \ p + c_{0} - s_{i} + V(k + 1, 1)\Big\rbrace \text{.}

Navedena jednakost je tražena dvoindeksna rekurzivna relacija uz pomoć koje se računaju vrijednosti funkcije V. Preostaje zadati početne uvjete, tj. neke vrijednosti funkcije V uz pomoć kojih se može izračunati svaka od preostalih vrijednosti te funkcije.

Da bi se mogli zadati početni uvjeti, razmatra se odluka koja se donosi na kraju razdoblja planiranja, odnosno početkom četvrte godine. Pripadna vrijednost varijable etape je k = 4, pa se zapravo zadaju vrijednosti V(4, i). Na kraju razdoblja planiranja moguća je točno jedna odluka: rashodovati dotad korišteno vozilo. To vozilo ne može biti novo, tj. ne može biti i_{\min} = 0, pa je najmanja moguća starost vozila jednaka i = 1. Najveća moguća starost vozila jest i = 5, pa se računaju vrijednosti V(4, i) za i = 1, 2, 3, 4, 5. Rezultat odluke rashodovati dotad korišteno vozilo je prihod jednak likvidacijskoj vrijednosti vozila na početku četvrte godine. Budući da minimiziramo ukupne troškove, prihod se formalno evidentira kao negativni trošak:

\begin{align*} V(4, 1) &= -s_{1} = -(25 - 5 \cdot 1) = -20 ; \\ V(4, 2) &= -s_{2} = -(25 - 5 \cdot 2) = -15 ; \\ V(4, 3) &= -s_{3} = -(25 - 5 \cdot 3) = -10 ; \\ V(4, 4) &= -s_{4} = -(25 - 5 \cdot 4) = -5 ; \\ V(4, 5) &= -s_{5} = -(25 - 5 \cdot 5) = 0 \text{.} \end{align*}

Zadavanjem navedenih vrijednosti moguće je izračunati svaku od preostalih vrijednosti funkcije V na temelju prethodno navedene rekurzivne relacije. Najprije se razmatra početak treće godine, odnosno etapa k = 3. Najveća moguća starost vozila u toj etapi je i = 4, pa se računaju vrijednosti V(3, i), za i = 1, 2, 3, 4:

\begin{align*} V(3, 1) &= \min \big\lbrace c_{1} + V(3 + 1, 1 + 1), \ p + c_{0} - s_{1} + V(3 + 1, 1)\big\rbrace \\ &= \min \big\lbrace 20 + V(4, 2), \ 60 + 10 - 20 + V(4, 1)\big\rbrace \\ &= \min \big\lbrace 20 + (-15), \ 50 + (-20)\big\rbrace = 5 ; \\ V(3, 2) &= \min \big\lbrace c_{2} + V(3 + 1, 2 + 1), \ p + c_{0} - s_{2} + V(3 + 1, 1)\big\rbrace \\ &= \min \big\lbrace 40 + V(4, 3), \ 60 + 10 - 15 + V(4, 1)\big\rbrace \\ &= \min \big\lbrace 40 + (-10), \ 55 + (-20)\big\rbrace = 30 ; \\ V(3, 3) &= \min \big\lbrace c_{3} + V(3 + 1, 3 + 1), \ p + c_{0} - s_{3} + V(3 + 1, 1)\big\rbrace \\ &= \min \big\lbrace 60 + V(4, 4), \ 60 + 10 - 10 + V(4, 1)\big\rbrace \\ &= \min \big\lbrace 60 + (-5), \ 60 + (-20)\big\rbrace = 40 ; \\ V(3, 4) &= \min \big\lbrace c_{4} + V(3 + 1, 4 + 1), \ p + c_{0} - s_{4} + V(3 + 1, 1)\big\rbrace \\ &= \min \big\lbrace 70 + V(4, 5), \ 60 + 10 - 5 + V(4, 1)\big\rbrace \\ &= \min \big\lbrace 70 + 0, \ 65 + (-20)\big\rbrace = 45 \text{.} \end{align*}

U sljedećoj fazi razmatra se početak druge godine, odnosno etapa k = 2. Najveća moguća starost vozila u toj etapi je i = 3, pa se računaju vrijednosti V(2, i), za i = 1, 2, 3:

\begin{align*} V(2, 1) &= \min \big\lbrace c_{1} + V(2 + 1, 1 + 1), \ p + c_{0} - s_{1} + V(2 + 1, 1)\big\rbrace \\ &= \min \big\lbrace 20 + V(3, 2), \ 60 + 10 - 20 + V(3, 1)\big\rbrace \\ &= \min \big\lbrace 20 + 30, \ 50 + 5\big\rbrace = 50 ; \\ V(2, 2) &= \min \big\lbrace c_{2} + V(2 + 1, 2 + 1), \ p + c_{0} - s_{2} + V(2 + 1, 1)\big\rbrace \\ &= \min \big\lbrace 40 + V(3, 3), \ 60 + 10 - 15 + V(3, 1)\big\rbrace \\ &= \min \big\lbrace 40 + 40, \ 55 + 5\big\rbrace = 60 ; \\ V(2, 3) &= \min \big\lbrace c_{3} + V(2 + 1, 3 + 1), \ p + c_{0} - s_{3} + V(2 + 1, 1)\big\rbrace \\ &= \min \big\lbrace 60 + V(3, 4), \ 60 + 10 - 10 + V(3, 1)\big\rbrace \\ &= \min \big\lbrace 60 + 45, \ 60 + 5\big\rbrace = 65 \text{.} \end{align*}

U sljedećoj fazi razmatra se početak prve godine, odnosno etapa k = 1. Najveća moguća starost vozila u toj etapi je i = 2, pa se radi potpunosti računaju vrijednosti V(1, i), za i = 1, 2:

\begin{align*} V(1, 1) &= \min \big\lbrace c_{1} + V(1 + 1, 1 + 1), \ p + c_{0} - s_{1} + V(1 + 1, 1)\big\rbrace \\ &= \min \big\lbrace 20 + V(2, 2), \ 60 + 10 - 20 + V(2, 1)\big\rbrace \\ &= \min \big\lbrace 20 + 60, \ 50 + 50\big\rbrace = 80 ; \\ V(1, 2) &= \min \big\lbrace c_{2} + V(1 + 1, 2 + 1), \ p + c_{0} - s_{2} + V(1 + 1, 1)\big\rbrace \\ &= \min \big\lbrace 40 + V(2, 3), \ 60 + 10 - 15 + V(2, 1)\big\rbrace \\ &= \min \big\lbrace 40 + 65, \ 55 + 50\big\rbrace = 105 \text{.} \end{align*}

Vrijednost V(1, 2) jednaka je 105, pa slijedi da ukupni minimalni troškovi korištenja vozila u razdoblju planiranja iznose 105 n.j. Vrijedi istaknuti da se ta vrijednost postiže i izborom alternative A_{1} i izborom alternative A_{2}, što znači da postoje ukupno dvije različite optimalne politike zamjene. Te se politike mogu lako «očitati» iz gore provedenih izračuna na sljedeći način:

1. optimalna politika zamjene

\bullet	početak 1. godine: zadržati vozilo staro dvije godine;
\bullet	početak 2. godine: vrijednost V(1, 2) = 105 u ovom je slučaju dobivena uz pomoć vrijednosti V(2, 3) = 65. Ta je vrijednost dobivena izborom alternative A_{2} na početku 2. godine, što znači da tada treba rashodovati dotad korišteno vozilo i kupiti novo;
\bullet	početak 3. godine: vrijednost V(2, 3) = 65 dobivena je uz pomoć vrijednosti V(3, 1) = 5. Ta je vrijednost dobivena izborom alternative A_{1} na početku 3. godine, što znači da tada treba zadržati dotad korišteno vozilo;
\bullet	početak 4. godine: rashodovati dotad korišteno vozilo.

2. optimalna politika zamjene

\bullet	početak 1. godine: rashodovati vozilo staro 2 godine i kupiti novo;
\bullet	početak 2. godine: vrijednost V(1, 2) = 105 u ovom je slučaju dobivena uz pomoć vrijednosti V(2, 1) = 50. Ta vrijednost dobivena je izborom alternative A_{1} na početku 2. godine, što znači da tada treba zadržati dotad korišteno vozilo;
\bullet	početak 3. godine: vrijednost V(2, 1) = 50 dobivena je uz pomoć vrijednosti V(3, 2) = 30. Ta je vrijednost dobivena izborom alternative A_{1} na početku 3. godine, što znači da tada treba zadržati dotad korišteno vozilo;
\bullet	početak 4. godine: rashodovati dotad korišteno vozilo.

U prethodnim su se primjerima nastojali minimizirati ukupni troškovi nastali korištenjem opreme. No, u praksi se vrlo često javljaju i problemi maksimizacije ukupne dobiti nastale korištenjem neke opreme. Postupak rješavanja takvih problema bit će ilustriran na sljedećim primjerima.

Primjer 4

Za opremu nekoga proizvodnog pogona koja osigurava nesmetan i neprekidan proces proizvodnje zadane su nabavna cijena p = 120 n.j. i funkcija neto dobiti, nastale korištenjem opreme (d). Nakon određenoga vremena korištenja opremu nije moguće prodati, pa početkom svake godine treba donijeti odluku o zamjeni ili zadržavanju dotadašnje opreme. Godišnja neto dobit od korištenja opreme zadana je kao funkcija starosti opreme (i):

d_{i} = d(i) = \begin{cases} 120-20 \cdot i, & \text{za }i=0\text{, }1\text{, }2\text{, }3\text{, }4\text{, }5\text{}; \\ 0, & \text{za }i \geq 6\text{.} \end{cases}

Treba odrediti optimalnu politiku zamjene opreme u razdoblju od n = 8 godina ako se na početku prve godine raspolaže opremom starom tri godine.

Analogno kao u prethodnom primjeru definira se realna funkcija V dviju cjelobrojnih varijabli s:

\begin{align*} V=V(k,i) = \ & \text{najveća ukupna neto dobit ostvarena od početka godine }k\text{ do} \\ & \text{kraja razdoblja planiranja ako se na početku godine }k\text{ raspolaže} \\ & \text{opremom starom }i\text{ godina.} \end{align*}

Budući da se na početku prve godine raspolaže opremom starom 3 godine, treba izračunati vrijednost V(1, 3). U tu svrhu najprije se određuje odgovarajuća dvoindeksna rekurzivna relacija i zadaju početni uvjeti.

Za određivanje rekurzivne relacije provodi se sljedeće zaključivanje: Pretpostavlja se da se na početku godine k koristi oprema stara i godina. Odluka na početku te godine je točno jedna od alternativa A_{1} = zadržati opremu još godinu dana i A_{2}= zamijeniti dotad korištenu opremu.

Ako se donese odluka A_{1}, tj. odluči li se zadržati opremu i koristiti se njome u cijeloj godini k (do početka godine k + 1), ukupna neto dobit u godini k koja proizlazi iz takve odluke jednaka je neto dobiti nastaloj korištenjem opreme stare i godina. Ta je neto dobit jednaka d_{i}. Sljedeća etapa u kojoj se donosi odluka je početak (k + 1) godine, a u tom trenutku raspolaže se opremom starom i + 1 godina. Najveća ukupna neto dobit od početka (k + 1) godine do kraja razdoblja planiranja, prema definiciji funkcije V, iznosi V(k + 1, i + 1). Prema tome, ukupna neto dobit nastala kao posljedica izbora alternative A_{1} na početku godine k iznosi d_{i} + V(k + 1, i + 1).

Ako se donese odluka A_{2}, tj. odluči li se zamijeniti oprema, u godini k pojavit će se trošak nabave nove opreme i neto dobit nastala korištenjem nove opreme. Trošak nabave nove opreme jednak je nabavnoj cijeni opreme, tj. p. Godišnja neto dobit nastala korištenjem nove opreme iznosi d_{0}. Stoga ukupna neto dobit u godini k iznosi d_{0} - p. Sljedeća etapa u kojoj se donosi odluka je početak (k + 1) godine, a u tom trenutku raspolaže se opremom starom jednu godinu. Najveća ukupna neto dobit od početka (k + 1) godine do kraja razdoblja planiranja, prema definiciji funkcije V, iznosi V(k + 1, 1). Prema tome, ukupna neto dobit nastala kao posljedica izbora alternative A_{2} na početku godine k iznosi d_{0} - p + V(k + 1, 1).

Budući da ukupnu neto dobit treba maksimizirati u svakoj pojedinoj etapi, iz navedenih razmatranja proizlazi sljedeća jednakost:

\begin{align*}V(k,i) &= \max \big\lbrace d_{i} + V(k + 1, i + 1), \ d_{0} - p + V(k + 1, 1) \big\rbrace \\ &= \max \big\lbrace d_{i} + V(k + 1, i + 1), \ 120 - 120 + V(k + 1, 1) \big\rbrace \\ &= \max \big\lbrace d_{i} + V(k + 1, i + 1), \ V(k + 1, 1) \big\rbrace \text{.}\end{align*}

Preostaje zadati početne uvjete. U tu se svrhu razmatra odluka koja se donosi početkom posljednje godine razdoblja planiranja, odnosno početkom osme godine. Pripadna vrijednost varijable etape je k = 8, pa se zapravo zadaju vrijednosti V(8, i). Najmanja moguća vrijednost varijable stanja je i_{\min} = 0 i postiže se ako se početkom 8. godine donese odluka o kupnji nove opreme. Najveća moguća vrijednost varijable stanja jednaka je i_{\max} = 3 + 7 = 10 i postiže se ako se oprema stara 3 godine zadrži tijekom svih osam godina. Budući da, prema definiciji funkcije V, za svaki k = 9, 10, 11, \ldots i svaki i \in \mathbb{N} vrijedi jednakost:

V(k,i)=0 ,

izraz za izračunavanje vrijednosti V(8, i) može se transformirati ovako:

\begin{align*}V(8, i) &= \max \big\lbrace d_{i} + V(8 + 1, i + 1), \ d_{0} - p + V(8 + 1, 1) \big\rbrace \\ &= \max \big\lbrace d_{i} + V(9, i + 1), \ 120 - 120 + V(9, 1) \big\rbrace \\ &= \max \big\lbrace d_{i} + 0, \ 0 \big\rbrace = d_{i} \text{.}\end{align*}

Dobiva se:

i	0	1	2	3	4	5	6	7	8	9	10
V(8,i)	120	100	80	60	40	20	0	0	0	0	0

U sljedećoj fazi računaju se vrijednosti V(7, i). U etapi k = 7, tj. početkom 7. godine najveća moguća vrijednost varijable stanja je i_{\max} = 3 + 6 = 9, pa se računaju vrijednosti V(7, i) za i = 0, 1, 2, \ldots, 8, 9. Koristeći se navedenom dvoindeksnom rekurzivnom relacijom, dobiva se:

\begin{align*} V(7, 0) &= \max \big\lbrace d_{0} + V(7 + 1, 0 + 1), \ V(7 + 1, 1) \big\rbrace \\ &= \max \big\lbrace 120 + V(8, 1), \ V(8, 1) \big\rbrace = \max \big\lbrace 120 + 100, \ 100 \big\rbrace = 220 ; \\ V(7, 1) &= \max \big\lbrace d_{1} + V(7 + 1, 1 + 1), \ V(7 + 1, 1) \big\rbrace \\ &= \max \big\lbrace 100 + V(8, 2), \ V(8, 1) \big\rbrace = \max \big\lbrace 100 + 80, \ 100 \big\rbrace = 180 ; \\ V(7, 2) &= \max \big\lbrace d_{2} + V(7 + 1, 2 + 1), \ V(7 + 1, 1) \big\rbrace \\ &= \max \big\lbrace 80 + V(8, 3), \ V(8, 1) \big\rbrace = \max \big\lbrace 80 + 60, \ 100 \big\rbrace = 140 ; \\ V(7, 3) &= \max \big\lbrace d_{3} + V(7 + 1, 3 + 1), \ V(7 + 1, 1) \big\rbrace \\ &= \max \big\lbrace 60 + V(8, 4), \ V(8, 1) \big\rbrace = \max \big\lbrace 60 + 40, \ 100 \big\rbrace = 100 ; \\ V(7, 4) &= V(7, 5) = V(7, 6) = V(7, 7) = V(7, 8) = V(7, 9) = V(8, 1) = 100 \end{align*}

(što znači da ako se početkom sedme godine raspolaže opremom starom barem 3 godine, svakako se isplati kupiti novu).
Analogno se postupa u svakoj od sljedećih šest faza. Dobivaju se sljedeće vrijednosti:

\begin{align*} V(6,0) & = 300, \ V(6,1) = 240, \ V(6,2) = 180, \\ V(6,3) & = V(6,4) = V(6,5) = V(6,6) = V(6,7) = V(6,8) = 180 \end{align*}

(što znači da ako se početkom šeste godine raspolaže opremom starom barem dvije godine, svakako se isplati kupiti novu);

\begin{align*} V(5,0) & = 360, \ V(5,1) = 280, \ V(5,2) = 260, \ V(5,3) = 240, \\ V(5,4) & = V(5,5) = V(5,6) = V(5,7) = 240 \end{align*}

(što znači da ako se početkom pete godine raspolaže opremom starom barem tri godine, svakako se isplati kupiti novu);

\begin{align*} V(4,0) & = 400, \ V(4,1) = 360, \ V(4,2) = 320, \ V(4,3) = 300, \ V(4,4) = 280, \\ V(4,5) &= V(4,6) = 280 \end{align*}

(što znači da ako se početkom četvrte godine raspolaže opremom starom barem četiri godine, svakako se isplati kupiti novu);

\begin{align*} V(3,0) & = 480, \ V(3,1) = 420, \ V(3,2) = 380, \ V(3,3) = 360, \\ V(3,4) &= V(3,5) = 360 \end{align*}

(što znači da ako se početkom treće godine raspolaže opremom starom barem tri godine, svakako se isplati kupiti novu);

V(2,0) = 540, \ V(2,1) = 480, \ V(2,2) = 440, \ V(2,3) = 420, \ V(2,4) = 420

(što znači da ako se početkom druge godine raspolaže opremom starom barem tri godine, svakako se isplati kupiti novu);

V(1,0) = 600, \ V(1,1) = 540, \ V(1,2) = 500, \ V(1,3) = 480\text{.}

Prema tome, tražena maksimalna ukupna neto dobit u cjelokupnom razdoblju planiranja iznosi 480 n.j. Preostaje odrediti optimalnu politiku zamjene opreme, odnosno «očitati» slijed odluka. Vrijednost V(1, 3) = 480 postiže se neovisno o izboru alternative (A_{1} ili A_{2}). Stoga se dobivaju sljedeće optimalne politike:

1. optimalna politika

\bullet	početak 1. godine: zadržati postojeću opremu;
\bullet	početak 2. godine: zamjena opreme;
\bullet	početak 3., početak 4. i početak 5. godine: zadržati postojeću opremu;
\bullet	početak 6. godine: zamjena opreme;
\bullet	početak 7. i početak 8. godine: zadržati postojeću opremu.

2. optimalna politika

\bullet	početak 1. godine: zadržati postojeću opremu;
\bullet	početak 2. godine: zamjena opreme;
\bullet	početak 3. i početak 4. godine: zadržati postojeću opremu;
\bullet	početak 5. godine: zamjena opreme;
\bullet	početak 6., početak 7. i početak 8. godine: zadržati postojeću opremu.

3. optimalna politika

\bullet	početak 1. godine: zamjena opreme;
\bullet	početak 2., početak 3. i početak 4. godine: zadržati postojeću opremu;
\bullet	početak 5. godine: zamjena opreme;
\bullet	početak 6., početak 7. i početak 8. godine: zadržati postojeću opremu.

Ako se unaprijed donese odluka da se na početku prve godine zamjenjuje dotad korištena oprema, postupak donošenja optimalne politike zamjene može se svesti na određivanje kritičnoga puta u težinskom digrafu. Navedeno je modeliranje moguće ako i samo ako je težina svakoga luka (i, j) za i \lt j pozitivan realan broj4. Postupak se prikazuje na sljedećem primjeru.

Primjer 5

Treba riješiti primjer 4 uz dodatan uvjet da se početkom prve godine obavezno nabavlja nova oprema. Odmah se može uočiti da će rješenje ovoga primjera biti 3. optimalna politika iz primjera 4.

Matematički model je potpuni težinski digraf čiji vrhovi označuju početke godina. Budući da je razdoblje planiranja dugo n = 8 godina, digraf će imati ukupno n + 1 = 8 + 1 = 9 vrhova: 1, 2, 3, 4, 5, 6, 7, 8, 9 (vrh 9 interpretiramo kao kraj 8. godine, odnosno kraj razdoblja planiranja). Vrhovi i i j bit će spojeni lukom od i prema j ako i samo ako je i \lt j, pa će graf imati ukupno \binom{9}{2} = 36 različitih lukova. Preostaje zadati težinu svakoga luka:

\begin{split} w_{ij} & = \text{(ukupna neto dobit nastala korištenjem opreme u godinama} \\ & \qquad \text{}i\text{, }i + 1\text{, }\ldots\text{, }j - 2\text{, }j - 1\text{)} - \text{(nabavna cijena opreme u godini }i\text{)} \\ & = \sum_{k=0}^{j-i-1}d_{k} - p_{i} . \end{split}

Budući da je d_{0} = p = 120 n.j, ukupna neto dobit u prvoj godini korištenja opreme jednaka je 0, pa za svaki i = 1, 2, 3, 4, 5, 6, 7, 8 vrijede jednakosti:

\begin{gather*} w_{i,i+1} = 0 , \\ w_{i,i+k} = \sum_{m=1}^{k-1}d_{k} , \ \text{ za svaki }k \in \mathbb{N} \setminus \lbrace 1\rbrace \text{ za koji postoji luk }(i,i+k)\text{.} \end{gather*}

Prema definiciji veličina d_{i}, za svaki i \in \mathbb{N} očito vrijedi nejednakost d_{i} \geq 0, pa je nužan uvjet za modeliranje problema potpunim težinskim digrafom ispunjen. Nadalje, zbog

\begin{align*} d_{1} & = 120 - 20 \cdot 1 = 100 ; & d_{5} & = 120 - 20 \cdot 5 = 20 ; \\ d_{2} & = 120 - 20 \cdot 2 = 80 ; & d_{6} & = 120 - 20 \cdot 6 = 0 ; \\ d_{3} & = 120 - 20 \cdot 3 = 60 ; & d_{7} & = 0 ; \\ d_{4} & = 120 - 20 \cdot 4 = 40 ; & d_{8} & = 0 , \end{align*}

slijedi:

\begin{align*} w_{12} & = w_{23} = w_{34} = w_{45} = w_{56} = w_{67} = w_{78} = w_{89} = 0 ; \\ w_{13} & = w_{24} = w_{35} = w_{46} = w_{57} = w_{68} = w_{79} = d_{1} = 100 ; \\ w_{14} & = w_{25} = w_{36} = w_{47} = w_{58} = w_{69} = d_{1} + d_{2} = 100 + 80 = 180 ; \\ w_{15} & = w_{26} = w_{37} = w_{48} = w_{59} = d_{1} + d_{2} + d_{3} = 100 + 80 + 60 = 240 ; \\ w_{16} & = w_{27} = w_{38} = w_{49} = d_{1} + d_{2} + d_{3} + d_{4} = 100 + 80 + 60 + 40 = 280 ; \\ w_{17} & = w_{28} = w_{39} = d_{1} + d_{2} + d_{3} + d_{4} + d_{5} = 100 + 80 + 60 + 40 + 20 = 300 ; \\ w_{18} & = w_{29} = d_{1} + d_{2} + d_{3} + d_{4} + d_{5} + d_{6} = 100 + 80 + 60 + 40 + 20 + 0 = 300 ; \\ w_{19} & = d_{1} + d_{2} + d_{3} + d_{4} + d_{5} + d_{6} +d_{7} = 100 + 80 + 60 + 40 + 20 + 0 + 0 = \\ & = 300 \text{.} \end{align*}

Uz pomoć računalnoga programa Grin dobiva se digraf prikazan na slici 3.

Slika 3: Model problema iz primjera 5.

Primjenom procedure Critical Path implementirane u istom računalnom programu određuje se kritični put u tom digrafu:

1 — 5 — 9.

Njegova je težina 480 i ona je jednaka optimalnoj ukupnoj neto dobiti. Jedini unutrašnji vrh u kritičnom putu je vrh 5, pa slijedi da početkom 5. godine treba zamijeniti dotadašnju opremu. Kad se tomu doda unaprijed postavljeni uvjet da se početkom prve godine obavezno kupuje nova oprema, dobiva se 3. optimalna politika dobivena u rješenju primjera 4.

Zaključno se može istaknuti kako se još neki tipovi logističkih problema također mogu riješiti uz pomoć modela i algoritama teorije grafova (vidjeti [4]).

Bibliografija

[1]	Schun–Chen Niu, Dynamic Programming, School of Management, University of Texas, Dallas, http://www.utdallas.edu/ scniu/OPRE-6201/documents/DP2-Equipment-Replacement.pdf, 15. 6. 2009.
[2]	Farid AitSahlia, Operations Research 2, Industrial and Systems Engineering, University of Florida, Weil Hall, http://www.ise.ufl.edu/esi4313/DP.ppt, 15. 6. 2009.
[3]	Michael Trick, Dynamic Programming, Tepper School of Business, Carnegie Mellon University, Pittsburg, http://mat.gsia.cmu.edu/classes/dynamic/node7.html, 15. 6. 2009.
[4]	Maja Fošner, Tomaž Kramberger, Teorija grafova i logistika, math.e, broj 14, http://e.math.hr/math_e_article/br14/fosner_kramberger, Zagreb, 2009.
[5]	Richard E. Bellman, Dynamic Programming, Courier Dover Publication, 2003.
[6]	Blaženka Divjak, Alen Lovrenčić, Diskretna matematika s teorijom grafova, FOI – TIVA, Varaždin, 2005.
[7]	Jovan Petrić, Operaciona istraživanja, Nauka, Beograd, 1997.
[8]	Jovan Petrić, Lazar Šarenac, Zdravko Kojić, Operaciona istraživanja – zbirka rešenih zadataka, Nauka, Beograd, 1996.

1Radi jednostavnosti, pretpostavlja se da su u navedenu cijenu uračunati svi pripadajući porezi, prirezi itd. n.j. je pokrata za novčanu jedinicu.

2Likvidacijska vrijednost nekoga sredstva je vrijednost rashodovanoga stalnog sredstva koja se dobije tako da se od tržišne cijene toga sredstva odbiju troškovi rashodovanja.

3Godišnji trošak održavanja automobila staroga točno 5 godina jednak je nuli. Naime, ako je početkom neke godine godine starost automobila točno 5 godina, obavezno odmah rashodujemo automobil kako bismo izbjegli daljnje troškove njegova održavanja.

4Ako je težina luka (i,j) negativan realan broj, luk (i,j) treba zamijeniti lukom (j,i) čija je težina pozitivan realan broj. Navedena zamjena može dovesti do nastanka ciklusa u grafu (osobito ako je graf potpun), a u takvim slučajevima traženi kritični put ne postoji.

math.e

Secondary links

Novi brojevi časopisa math.e

Matematička događanja

Kalendar

Prosinac

Matematički blogovi

Sponzori

optimizacija

Prepoznavanje lica pomoću tenzorske dekompozicije singularnih vrijednosti

Floyd-Warshallov algoritam u tropskoj geometriji

Boroj 30

Formule za udaljenost točke do pravca u ravnini, u smislu lp - udaljenosti, 1 ≤ p ≤ ∞.

27. broj časopisa e.math

Genetski algoritmi i biomorfi

Kvantitativne metode odlučivanja - problem složene razdiobe ulaganja

Zaključak

Kvantitativne metode odlučivanja – problem jednostavne razdiobe ulaganja

Bojan Kovačić i Tihana Strmečki, Tehničko veleučilište, Zagreb

Kvantitativne metode odlučivanja – problem optimalne zamjene opreme