Kvantitativne metode odlučivanja – problem optimalne zamjene opreme
Problem optimalne zamjene opreme jedan je od osnovnih problema u cjelokupnoj industriji. Sastoji se u određivanju optimalnoga trenutka zamjene stare opreme novom pod uvjetima da se opseg proizvodnje poveća, a troškovi proizvodnje umanje, tako da se time potpuno nadoknade troškovi kupnje nove opreme, gubici uzrokovani zastojem u proizvodnji zbog uvođenja nove opreme i troškovi obuke djelatnika za rad na novoj opremi.
Temeljni zadatak je odrediti optimalnu politiku modernizacije i zamjene opreme prihvaćajući pritom različite uvjete vezane za tekuće održavanje, karakteristike proizvodnje i predviđeni tehnološki razvoj. Ovakav proces očito zahtijeva analizu u više faza, pa se time dinamičko programiranje nameće kao prikladan način rješavanja ovakvih problema.
Neki tipovi problema zamjene opreme i načini njihova rješavanja ilustriraju se na sljedećim primjerima. U rješenjima pojedinih primjera koriste se računalni programi Graph Magics i Grin čije su besplatne probne (trial) verzije dostupne za preuzimanje putem Interneta.
Primjer 1
Utvrđena poslovna politika neke tvrtke predviđa korištenje automobila u sljedećih n = 5 godina, pa je na početku prve godine razdoblja planiranja kupljen novi automobil po nabavnoj cijeni od p = 12 n.j.1 Radi jednostavnosti, pretpostavlja se da je nabavna cijena automobila stalna tijekom cijeloga razdoblja planiranja te da će po isteku razdoblja planiranja automobil obavezno biti rashodovan. Godišnji neto troškovi održavanja automobila (c_{i}) i likvidacijska vrijednost2 automobila (s_{i}) iskazani su kao funkcija starosti automobila:
| starost automobila (i) [god.] | 0 | 1 | 2 | 3 | 4 | 5 |
| godišnji neto trošak održavanja (c_{i}) [n.j.] | 2 | 4 | 5 | 9 | 12 | 12 |
| likvidacijska vrijednost (s_{i}) [n.j.] | - | 7 | 6 | 2 | 1 | 0 |
Niz (c_{i})_{i \in \mathbb{N}} nužno je rastući, tj. povećanjem starosti automobila povećavaju se i godišnji troškovi njegova održavanja. Zbog tog razloga nakon određenog vremena može biti ekonomski isplativije rashodovati do tada korišteni automobil i kupiti novi. S druge je strane niz (s_{i})_{i \in \mathbb{N}} nužno padajući, tj. povećanjem starosti automobila smanjuje se njegova likvidacijska vrijednost.
Politika zamjene u ovome je slučaju donošenje odluke treba li zadržati postojeći automobil ili ga rashodovati i kupiti novi automobil. Navedeno odlučivanje na dnevni red dolazi početkom svake pojedine godine. Najjednostavniji primjeri politika zamjene su:
| P_{1}) zamjena automobila, tj. rashodovanje do tada korištenoga automobila i kupnja novoga početkom svake pojedine godine (tj. početkom druge, treće, četvrte i pete godine); |
| P_{2}) zadržavanje postojećeg automobila sve do kraja pete godine. |
Optimalna politika zamjene je politika zamjene koja osigurava najmanje ukupne neto troškove uporabe automobila tijekom svih pet godina. U promatranom primjeru to znači ispitati svih 16 međusobno različitih politika zamjene i među njima odrediti najbolju. No, takva je metoda za iole veće vrijednosti n općenito vrlo spora i neučinkovita, pa se stoga nameće problem iznalaženja dovoljno učinkovitih metoda i algoritama za određivanje optimalne politike. U tu se svrhu primjenjuju metode i tehnike dinamičkoga programiranja.
Primjer
\binom{n+1}{2}=\binom{6}{2} = 15 \text{.}
Preostaje definirati težinu svakog od dobivenih lukova. Budući da treba minimizirati ukupne neto troškove, težina w_{ij} luka (i, j) definira se kao:
\begin{split} w_{ij}&= (\text{nabavna cijena automobila na početku godine } i)\\ &\quad + (\text{troškovi održavanja u godinama } i, i + 1, \ldots, j - 1) \\ &\quad - (\text{likvidacijska vrijednost automobila na početku godine } j). \end{split}
Odatle slijedi da je analitički izraz za izračunavanje težina w_{ij}:
w_{ij} = p_{i} + c_{0} + c_{1} + \ldots + c_{j-1-i}-s_{j-i} = p_{i} + \sum_{k=0}^{j-i-1}c_{k} - s_{j-i}.
Ovdje prešutno pretpostavljamo da se kraj godine k podudara s početkom godine (k + 1).
U razmatranom se primjeru pretpostavlja da je nabavna cijena automobila na početku svake godine ista i jednaka 12 n.j., tj. vrijedi jednakost p_{1} = p_{2} = p_{3} = p_{4} = p_{5} = p = 12. Zbog toga vrijedi i jednakost:
w_{ij} = w_{i+k,j+k} ,
za sve i,j,k za koje su definirane obje strane jednakosti. Tako se dobiva:
\begin{align*} w_{12}& = w_{23} = w_{34} = w_{45} = w_{56} = p + c_{0} - s_{1} = 12+2-7 = 7 ; \\ w_{13}& = w_{24} = w_{35} = w_{46} = p + (c_{0} + c_{1}) - s_{2} = 12+2+4-6 = 12 ; \\ w_{14}& = w_{25} = w_{36} = p + (c_{0} + c_{1} + c_{2}) - s_{3} = 12+2+4+5-2 = 21 ; \\ w_{15}& = w_{26} = p + (c_{0} + c_{1} + c_{2} + c_{3}) - s_{4} = 12+2+4+5+9-1 = 31 ; \\ w_{16}& = p + (c_{0} + c_{1} + c_{2} + c_{3} + c_{4}) - s_{5} = 12+2+4+5+9+12-0 = 44 \text{.} \end{align*}
Za rješavanje primjera u nastavku koristimo se računalnim programom Graph Magics. Koristeći se njime, modeliramo navedeni problem potpunim težinskim digrafom, koji je prikazan na slici
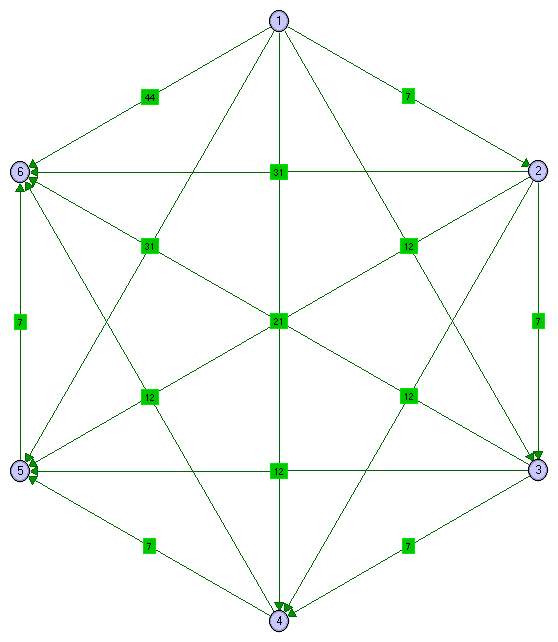
Slika 1:
Model problema iz primjera 1 .
Radi određivanja najkraćega puta, vrh 1 označi se kao početni vrh, a vrh 6 kao završni vrh. Koristeći se procedurom Find Shortest Path (from Start Vertex to End) određuje se najkraći put između vrhova 1 i 6:
1 — 2 — 4 — 6.
Njegova je težina jednaka 31. Unutrašnji vrhovi dobivenoga najkraćeg puta su 2 i 4, što znači da početkom tih godina treba rashodovati dotad korišteni automobil i zamijeniti ga novim. Prema tome, optimalna politika zamjene glasi:
| \bullet | početak 2. godine: rashodovanje dotad korištenog automobila i kupnja novoga; |
| \bullet | početak 3. godine: zadržavanje dotad korištenog automobila; |
| \bullet | početak 4. godine: rashodovanje dotad korištenog automobila i kupnja novoga; |
| \bullet | početak 5. godine: zadržavanje dotad korištenog automobila; |
| \bullet | kraj 5. godine/početak 6. godine: rashodovanje dotad korištenog automobila. |
Rješavanje «klasičnim» putem daje još jedan najkraći put:
1 — 3 — 5 — 6.
U ovom slučaju na početku treće i na početku pete godine razdoblja planiranja treba rashodovati dotad korišteni automobil i zamijeniti ga novim, tj. optimalna politika zamjene glasi:
| \bullet | početak 2. godine: zadržavanje dotad korištenog automobila; |
| \bullet | početak 3. godine: rashodovanje dotad korištenog automobila i kupnja novoga; |
| \bullet | početak 4. godine: zadržavanje dotad korištenog automobila; |
| \bullet | početak 5. godine: rashodovanje dotad korištenog automobila i kupnja novoga; |
| \bullet | kraj 5. godine/početak 6. godine: rashodovanje dotad korištenog automobila. |
Obje navedene optimalne politike postižu najmanji iznos ukupnih neto troškova 31 n.j.
Primjer 2
Usporedno s redovnim studiranjem Ivan je putem Student–servisa dobio honorarni posao dostavljača lokalnih besplatnih novina, oglasnoga materijala itd. Za taj mu je posao potreban bicikl koji trenutačno ne posjeduje. Trenutačna cijena novoga bicikla je p = 500 n.j. Novi bicikl može se koristiti najviše 3 godine, a potom ga treba prodati. Godišnji neto trošak održavanja bicikla i likvidacijska vrijednost bicikla, iskazani kao funkcije starosti bicikla, navedeni su u sljedećoj tablici:
| starost bicikla (i) [god.] | 0 | 1 | 2 | 3 |
| godišnji neto trošak (c_{i}) [n.j.] | 30 | 40 | 60 | - |
| likvidacijska vrijednost (s_{i}) [n.j.] | - | 400 | 300 | 250 |
Ako Ivan namjerava završiti svoj studij za točno 5 godina i dotad honorarno raditi kao dostavljač, treba odrediti optimalnu politiku zamjene bicikla tijekom razdoblja od 5 godina (pretpostavlja se da je cijena novoga bicikla stalna u cjelokupnom razdoblju planiranja te da će Ivan na kraju razdoblja planiranja obavezno prodati bicikl).
Prije rješavanja zadatka korisno je napraviti jednostavnu analizu kojom se pokušava utvrditi koje je «trajanje vlasništva» najekonomičnije, tj. je li općenito bolje zadržati bicikl 1, 2 ili 3 godine?
Kupi li Ivan bicikl, bude li ga koristio jednu godinu i potom ga prodao, prosječan (zapravo ukupan) godišnji neto trošak iznosit će p + c_{0} - s_{1} = 500 + 30 - 400 = 130 n.j.
Kupi li Ivan bicikl, bude li ga koristio ukupno dvije godine i potom ga prodao, prosječan godišnji neto trošak iznosit će
\frac{p + (c_{0} + c_{1}) - s_{2}}{2} = \frac{500 + (30 + 40) - 300}{2} = 135 \text{ n.j.}
Ako Ivan kupi bicikl, bude li ga koristio sve tri godine i potom ga prodao, prosječan godišnji neto trošak iznosit će
\frac{p + (c_{0} + c_{1} + c_{2}) - s_{3}}{3} = \frac{500 + (30 + 40 + 60) - 250}{3} = 126.67 \text{ n.j.}
Ova analiza pokazuje da je najisplativije zadržati bicikl sve tri godine i potom ga prodati, a ako to nije moguće, onda je najisplativije zadržati bicikl točno jednu godinu. Budući da je razdoblje planiranja n = 5 godina, može se procijeniti da će optimalna politika zamjene biti «kombinacija» jednogodišnjeg i trogodišnjeg trajanja vlasništva.
I u ovom se slučaju problem modelira težinskim digrafom, ali taj digraf neće biti potpun. Naime, bicikl se može koristiti najviše tri godine, a to je razdoblje strogo manje od razdoblja planiranja. Stoga neki vrhovi digrafa neće biti spojeni niti jednom spojnicom. Vrhovi digrafa ponovo će označavati početke godina, pa će graf imati ukupno n + 1 = 6 vrhova. Vrh i označavat će početak godine i (pritom se pretpostavlja da se kraj pete godine podudara s početkom šeste godine). Budući da se bicikl može koristiti najviše 3 godine, luk (i, j) postoji ako i samo ako vrijedi nejednakost 0 \lt j - i \leq 3. Stoga je skup svih lukova grafa jednak E = \lbrace (1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5)\rbrace. Težine pojedinih lukova izračunavaju se kao u primjeru
\begin{align*} w_{12}& = w_{23} = w_{34} = w_{45} = w_{56} = p + c_{0} - s_{1} = 500+30-400 = 130 ; \\ w_{13}& = w_{24} = w_{35} = w_{46} = p + (c_{0} + c_{1}) - s_{2} = 500+(30+40)-300 = 270 ; \\ w_{14}& = w_{25} = w_{36} = p + (c_{0} + c_{1} + c_{2}) - s_{3} = 500+(30+40+60)-250 = 380 \text{.} \end{align*}
Težinski digraf dobiven uz pomoć programa Graph Magics prikazan je na slici
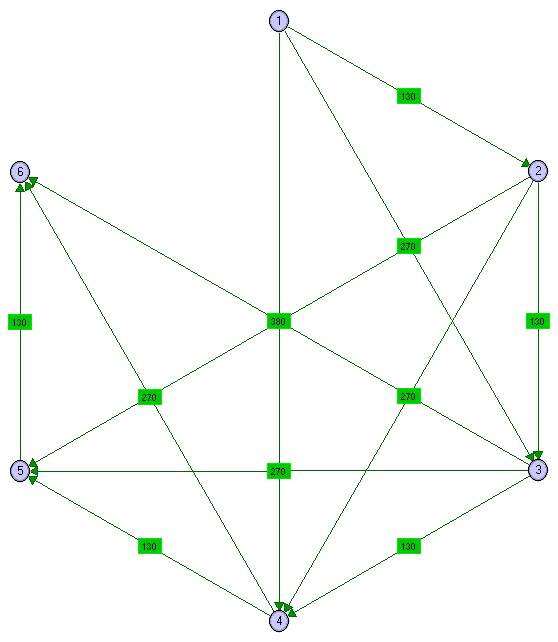
Slika 2:
Model problema iz primjera 2 .
Najkraći put između vrhova 1 i 6 je
1 — 2 — 3 — 6,
čija je težina 640. Prema tome, optimalna politika zamjene bicikla je sljedeća:
| \bullet | početak 2. godine: prodaja dotad korištenoga bicikla i kupnja novoga bicikla; |
| \bullet | početak 3. godine: prodaja dotad korištenoga bicikla i kupnja novoga bicikla; |
| \bullet | početak 4. godine: zadržavanje dotad korištenoga bicikla; |
| \bullet | početak 5. godine: zadržavanje dotad korištenoga bicikla; |
| \bullet | kraj 5. godine/početak 6. godine: prodaja dotad korištenoga bicikla. |
Dobivena optimalna politika uistinu je kombinacija trajanja vlasništva od jedne, odnosno tri godine, tj. navedenoj optimalnoj politici odgovara rastav 5 = 1 + 1 + 3. Vrijedi istaknuti da je ukupan broj različitih optimalnih politika jednak ukupnom broju različitih načina na koji se broj 5 može napisati kao zbroj barem jedne «jedinice» i barem jedne «trojke», a taj je jednak 3. Ti načini su: 1 + 1 + 3, 1 + 3 + 1, 3 + 1 + 1 i svaki od njih generira jednu optimalnu politiku (prvi način generira gore navedenu optimalnu politiku, drugi način generira optimalnu politiku kupnje novoga bicikla u 2. i 5. godini, a treći optimalnu politiku kupnje novoga bicikla u 4. i 5. godini). Sve tri optimalne politike daju iste minimalne ukupne neto troškove u iznosu od 640 n.j.
U prethodnim primjerima razmatrani su slučajevi u kojima je na početku prve godine već bila donesena odluka o kupnji nove opreme (automobila, bicikla), pa su se sve ostale odluke donosile na početku svake od sljedećih n godina (tu uključujemo i završnu odluku o rashodovanju opreme). Međutim, u praksi se nerijetko javljaju slučajevi u kojima na početku prve godine već raspolažemo s opremom starom i godina, čiji je vijek trajanja ukupno n godina, pa treba razmotriti optimalnu politiku zamjene u sljedećih n - i godina. I u takvim se slučajevima problem zamjene opreme može svesti na problem najkraćega puta u digrafu, no, u takvom se grafu pojavljuju negativne težine lukova i višestruki lukovi između dvaju vrhova, pa navedeni problem nije moguće riješiti uz pomoć računalnoga programa Graph Magics. Stoga će se takav problem riješiti «klasično» ilustrirajući tehniku dinamičkoga programiranja koja se ovdje primjenjuje.
Primjer 3
Pretpostavlja se da se na početku prve godine raspolaže vozilom starim dvije godine. Vozilo je potrebno koristiti u sljedeće n = 3 godine, pri čemu se na početku svake godine (uračunavajući i prvu!) donosi odluka: zadržati postojeće vozilo još godinu dana ili rashodovati postojeće vozilo i kupiti novo. Kao i prije, godišnji trošak održavanja vozila zadan je tablično kao funkcija starosti automobila:
| starost automobila (i) [god.] | 0 | 1 | 2 | 3 | 4 |
| godišnji neto trošak (c_{i}) [n.j.] | 10 | 20 | 40 | 60 | 70 |
Nadalje, cijena novoga vozila u sve je tri godine stalna i iznosi p = 60 n.j. Likvidacijska neto vrijednost automobila starog i godina zadana je funkcijom:
s_{i} = s(i) = 25 - 5 \cdot i \text{, za } i=1,2,3,4,5 \text{.}
Treba odrediti optimalnu politiku zamjene automobila u cjelokupnom razdoblju planiranja. Ukupan broj različitih politika zamjene jednak je 2^{n} = 2^{3} = 8 jer početkom svake godine donosimo jednu od dviju mogućih odluka.
Prvi korak u rješavanju problema je definiranje funkcije optimalne vrijednosti V=V(k,i) s:
\begin{align*} V(k,i) = \ & \text{najmanji ukupni neto troškovi od početka godine }k\text{ do kraja} \\ & \text{razdoblja planiranja (tj. početka godine }n + 1\text{) ako na početku} \\ & \text{godine }k\text{ raspolažemo vozilom starosti }i\text{.} \end{align*}
Funkcija V je funkcija dviju cjelobrojnih (točnije, prirodnih) varijabli: k i i. Varijabla k naziva se varijabla etape i ona «mjeri» razdoblja (etape) u kojima se donosi točno jedna odluka. U ovom slučaju varijabla etape poprima vrijednosti iz skupa \lbrace 1, 2, 3, 4\rbrace jer će se početkom 1., 2., 3. i 4. godine donositi odluka o zadržavanju ili rashodovanju vozila. Treba primijetiti da će početkom (n + 1)–te, tj. 4. godine biti donesena odluka o rashodovanju vozila jer će završiti planirano razdoblje u kojemu se želi koristiti vozilo. Varijabla i naziva se varijabla stanja i ona «mjeri» starost vozila na početku godine k. Ta će varijabla poprimati vrijednosti iz skupa \lbrace 1, 2, 3, 4, 5\rbrace jer najveća moguća starost vozila iznosi i_{\max} = 2 + 3 = 5 godina3.
Iz postavke navedenoga primjera slijedi da treba izračunati vrijednost V(1, 2) jer se na početku prve godine (k = 1) raspolaže vozilom starosti i = 2 godine. Navedena se vrijednost izračunava tako da se najprije definira dvoindeksna rekurzivna relacija koju zadovoljavaju vrijednosti V(k, i), a potom početni uvjeti koji omogućuju računanje konkretnih vrijednosti te funkcije.
Spomenuta dvoindeksna rekurzivna relacija dobiva se na sljedeći način: Pretpostavimo da se na početku godine k koristi vozilo staro i godina. Moguće su točno dvije alternative: A_{1}= zadržati vozilo još godinu dana i A_{2}= rashodovati vozilo i zamijeniti ga novim vozilom.
Ako se donese odluka A_{1}, tj. odluči li se zadržati vozilo i koristiti se njime u cijeloj godini k (do početka godine k + 1), ukupni neto trošak u godini k koji proizlazi iz takve odluke tvori isključivo neto trošak održavanja automobila starog i godina. Taj je trošak jednak c_{i}. Sljedeća etapa u kojoj se donosi odluka je početak (k + 1) godine, a u tom trenutku na raspolaganju će biti vozilo starosti i + 1 godina. Najmanji ukupni neto troškovi od početka (k + 1) godine do kraja razdoblja planiranja, prema definiciji funkcije V, iznose V(k + 1, i + 1). Prema tome, ukupni neto troškovi nastali kao posljedica izbora alternative A_{1} na početku godine k iznose c_{i} + V(k + 1, i + 1).
Ako se donese odluka A_{2}, tj. odluči li se rashodovati dotad korišteno vozilo i kupiti novo, u godini k pojavljuju se trošak nabave novoga vozila, godišnji trošak njegova održavanja te prihod dobiven rashodovanjem i prodajom dotadašnjega vozila, tj. prihod jednak likvidacijskoj vrijednosti dotadašnjega vozila. Trošak nabave novoga vozila jednak je njegovoj nabavnoj cijeni, tj. p. Godišnji neto trošak održavanja novoga vozila iznosi c_{0}, a likvidacijska vrijednost dotadašnjega vozila (staroga i godina) iznosi s_{i}. Stoga ukupni neto troškovi u godini k iznose p + c_{0} - s_{i}. Sljedeća etapa u kojoj se donosi odluka je početak (k + 1) godine, a u tom trenutku na raspolaganju je vozilo staro jednu godinu. Najmanji ukupni neto troškovi od početka (k + 1) godine do kraja razdoblja planiranja, prema definiciji funkcije V, iznose V(k + 1, 1). Prema tome, ukupni neto troškovi nastali kao posljedica izbora alternative A_{2} na početku godine k iznose p + c_{0} - s_{i} + V(k + 1, 1).
Budući da ukupne neto troškove treba minimizirati u svakoj pojedinoj etapi, iz navedenih razmatranja proizlazi sljedeća jednakost:
V(k, i) = \min \Big\lbrace c_{i} + V(k + 1, i + 1), \ p + c_{0} - s_{i} + V(k + 1, 1)\Big\rbrace \text{.}
Navedena jednakost je tražena dvoindeksna rekurzivna relacija uz pomoć koje se računaju vrijednosti funkcije V. Preostaje zadati početne uvjete, tj. neke vrijednosti funkcije V uz pomoć kojih se može izračunati svaka od preostalih vrijednosti te funkcije.
Da bi se mogli zadati početni uvjeti, razmatra se odluka koja se donosi na kraju razdoblja planiranja, odnosno početkom četvrte godine. Pripadna vrijednost varijable etape je k = 4, pa se zapravo zadaju vrijednosti V(4, i). Na kraju razdoblja planiranja moguća je točno jedna odluka: rashodovati dotad korišteno vozilo. To vozilo ne može biti novo, tj. ne može biti i_{\min} = 0, pa je najmanja moguća starost vozila jednaka i = 1. Najveća moguća starost vozila jest i = 5, pa se računaju vrijednosti V(4, i) za i = 1, 2, 3, 4, 5. Rezultat odluke rashodovati dotad korišteno vozilo je prihod jednak likvidacijskoj vrijednosti vozila na početku četvrte godine. Budući da minimiziramo ukupne troškove, prihod se formalno evidentira kao negativni trošak:
\begin{align*} V(4, 1) &= -s_{1} = -(25 - 5 \cdot 1) = -20 ; \\ V(4, 2) &= -s_{2} = -(25 - 5 \cdot 2) = -15 ; \\ V(4, 3) &= -s_{3} = -(25 - 5 \cdot 3) = -10 ; \\ V(4, 4) &= -s_{4} = -(25 - 5 \cdot 4) = -5 ; \\ V(4, 5) &= -s_{5} = -(25 - 5 \cdot 5) = 0 \text{.} \end{align*}
Zadavanjem navedenih vrijednosti moguće je izračunati svaku od preostalih vrijednosti funkcije V na temelju prethodno navedene rekurzivne relacije. Najprije se razmatra početak treće godine, odnosno etapa k = 3. Najveća moguća starost vozila u toj etapi je i = 4, pa se računaju vrijednosti V(3, i), za i = 1, 2, 3, 4:
\begin{align*} V(3, 1) &= \min \big\lbrace c_{1} + V(3 + 1, 1 + 1), \ p + c_{0} - s_{1} + V(3 + 1, 1)\big\rbrace \\ &= \min \big\lbrace 20 + V(4, 2), \ 60 + 10 - 20 + V(4, 1)\big\rbrace \\ &= \min \big\lbrace 20 + (-15), \ 50 + (-20)\big\rbrace = 5 ; \\ V(3, 2) &= \min \big\lbrace c_{2} + V(3 + 1, 2 + 1), \ p + c_{0} - s_{2} + V(3 + 1, 1)\big\rbrace \\ &= \min \big\lbrace 40 + V(4, 3), \ 60 + 10 - 15 + V(4, 1)\big\rbrace \\ &= \min \big\lbrace 40 + (-10), \ 55 + (-20)\big\rbrace = 30 ; \\ V(3, 3) &= \min \big\lbrace c_{3} + V(3 + 1, 3 + 1), \ p + c_{0} - s_{3} + V(3 + 1, 1)\big\rbrace \\ &= \min \big\lbrace 60 + V(4, 4), \ 60 + 10 - 10 + V(4, 1)\big\rbrace \\ &= \min \big\lbrace 60 + (-5), \ 60 + (-20)\big\rbrace = 40 ; \\ V(3, 4) &= \min \big\lbrace c_{4} + V(3 + 1, 4 + 1), \ p + c_{0} - s_{4} + V(3 + 1, 1)\big\rbrace \\ &= \min \big\lbrace 70 + V(4, 5), \ 60 + 10 - 5 + V(4, 1)\big\rbrace \\ &= \min \big\lbrace 70 + 0, \ 65 + (-20)\big\rbrace = 45 \text{.} \end{align*}
U sljedećoj fazi razmatra se početak druge godine, odnosno etapa k = 2. Najveća moguća starost vozila u toj etapi je i = 3, pa se računaju vrijednosti V(2, i), za i = 1, 2, 3:
\begin{align*} V(2, 1) &= \min \big\lbrace c_{1} + V(2 + 1, 1 + 1), \ p + c_{0} - s_{1} + V(2 + 1, 1)\big\rbrace \\ &= \min \big\lbrace 20 + V(3, 2), \ 60 + 10 - 20 + V(3, 1)\big\rbrace \\ &= \min \big\lbrace 20 + 30, \ 50 + 5\big\rbrace = 50 ; \\ V(2, 2) &= \min \big\lbrace c_{2} + V(2 + 1, 2 + 1), \ p + c_{0} - s_{2} + V(2 + 1, 1)\big\rbrace \\ &= \min \big\lbrace 40 + V(3, 3), \ 60 + 10 - 15 + V(3, 1)\big\rbrace \\ &= \min \big\lbrace 40 + 40, \ 55 + 5\big\rbrace = 60 ; \\ V(2, 3) &= \min \big\lbrace c_{3} + V(2 + 1, 3 + 1), \ p + c_{0} - s_{3} + V(2 + 1, 1)\big\rbrace \\ &= \min \big\lbrace 60 + V(3, 4), \ 60 + 10 - 10 + V(3, 1)\big\rbrace \\ &= \min \big\lbrace 60 + 45, \ 60 + 5\big\rbrace = 65 \text{.} \end{align*}
U sljedećoj fazi razmatra se početak prve godine, odnosno etapa k = 1. Najveća moguća starost vozila u toj etapi je i = 2, pa se radi potpunosti računaju vrijednosti V(1, i), za i = 1, 2:
\begin{align*} V(1, 1) &= \min \big\lbrace c_{1} + V(1 + 1, 1 + 1), \ p + c_{0} - s_{1} + V(1 + 1, 1)\big\rbrace \\ &= \min \big\lbrace 20 + V(2, 2), \ 60 + 10 - 20 + V(2, 1)\big\rbrace \\ &= \min \big\lbrace 20 + 60, \ 50 + 50\big\rbrace = 80 ; \\ V(1, 2) &= \min \big\lbrace c_{2} + V(1 + 1, 2 + 1), \ p + c_{0} - s_{2} + V(1 + 1, 1)\big\rbrace \\ &= \min \big\lbrace 40 + V(2, 3), \ 60 + 10 - 15 + V(2, 1)\big\rbrace \\ &= \min \big\lbrace 40 + 65, \ 55 + 50\big\rbrace = 105 \text{.} \end{align*}
Vrijednost V(1, 2) jednaka je 105, pa slijedi da ukupni minimalni troškovi korištenja vozila u razdoblju planiranja iznose 105 n.j. Vrijedi istaknuti da se ta vrijednost postiže i izborom alternative A_{1} i izborom alternative A_{2}, što znači da postoje ukupno dvije različite optimalne politike zamjene. Te se politike mogu lako «očitati» iz gore provedenih izračuna na sljedeći način:
1. optimalna politika zamjene
| \bullet | početak 1. godine: zadržati vozilo staro dvije godine; |
| \bullet | početak 2. godine: vrijednost V(1, 2) = 105 u ovom je slučaju dobivena uz pomoć vrijednosti V(2, 3) = 65. Ta je vrijednost dobivena izborom alternative A_{2} na početku 2. godine, što znači da tada treba rashodovati dotad korišteno vozilo i kupiti novo; |
| \bullet | početak 3. godine: vrijednost V(2, 3) = 65 dobivena je uz pomoć vrijednosti V(3, 1) = 5. Ta je vrijednost dobivena izborom alternative A_{1} na početku 3. godine, što znači da tada treba zadržati dotad korišteno vozilo; |
| \bullet | početak 4. godine: rashodovati dotad korišteno vozilo. |
| \bullet | početak 1. godine: rashodovati vozilo staro 2 godine i kupiti novo; |
| \bullet | početak 2. godine: vrijednost V(1, 2) = 105 u ovom je slučaju dobivena uz pomoć vrijednosti V(2, 1) = 50. Ta vrijednost dobivena je izborom alternative A_{1} na početku 2. godine, što znači da tada treba zadržati dotad korišteno vozilo; |
| \bullet | početak 3. godine: vrijednost V(2, 1) = 50 dobivena je uz pomoć vrijednosti V(3, 2) = 30. Ta je vrijednost dobivena izborom alternative A_{1} na početku 3. godine, što znači da tada treba zadržati dotad korišteno vozilo; |
| \bullet | početak 4. godine: rashodovati dotad korišteno vozilo. |
U prethodnim su se primjerima nastojali minimizirati ukupni troškovi nastali korištenjem opreme. No, u praksi se vrlo često javljaju i problemi maksimizacije ukupne dobiti nastale korištenjem neke opreme. Postupak rješavanja takvih problema bit će ilustriran na sljedećim primjerima.
Primjer 4
Za opremu nekoga proizvodnog pogona koja osigurava nesmetan i neprekidan proces proizvodnje zadane su nabavna cijena p = 120 n.j. i funkcija neto dobiti, nastale korištenjem opreme (d). Nakon određenoga vremena korištenja opremu nije moguće prodati, pa početkom svake godine treba donijeti odluku o zamjeni ili zadržavanju dotadašnje opreme. Godišnja neto dobit od korištenja opreme zadana je kao funkcija starosti opreme (i):
d_{i} = d(i) = \begin{cases} 120-20 \cdot i, & \text{za }i=0\text{, }1\text{, }2\text{, }3\text{, }4\text{, }5\text{}; \\ 0, & \text{za }i \geq 6\text{.} \end{cases}
Treba odrediti optimalnu politiku zamjene opreme u razdoblju od n = 8 godina ako se na početku prve godine raspolaže opremom starom tri godine.
Analogno kao u prethodnom primjeru definira se realna funkcija V dviju cjelobrojnih varijabli s:
\begin{align*} V=V(k,i) = \ & \text{najveća ukupna neto dobit ostvarena od početka godine }k\text{ do} \\ & \text{kraja razdoblja planiranja ako se na početku godine }k\text{ raspolaže} \\ & \text{opremom starom }i\text{ godina.} \end{align*}
Budući da se na početku prve godine raspolaže opremom starom 3 godine, treba izračunati vrijednost V(1, 3). U tu svrhu najprije se određuje odgovarajuća dvoindeksna rekurzivna relacija i zadaju početni uvjeti.
Za određivanje rekurzivne relacije provodi se sljedeće zaključivanje: Pretpostavlja se da se na početku godine k koristi oprema stara i godina. Odluka na početku te godine je točno jedna od alternativa A_{1} = zadržati opremu još godinu dana i A_{2}= zamijeniti dotad korištenu opremu.
Ako se donese odluka A_{1}, tj. odluči li se zadržati opremu i koristiti se njome u cijeloj godini k (do početka godine k + 1), ukupna neto dobit u godini k koja proizlazi iz takve odluke jednaka je neto dobiti nastaloj korištenjem opreme stare i godina. Ta je neto dobit jednaka d_{i}. Sljedeća etapa u kojoj se donosi odluka je početak (k + 1) godine, a u tom trenutku raspolaže se opremom starom i + 1 godina. Najveća ukupna neto dobit od početka (k + 1) godine do kraja razdoblja planiranja, prema definiciji funkcije V, iznosi V(k + 1, i + 1). Prema tome, ukupna neto dobit nastala kao posljedica izbora alternative A_{1} na početku godine k iznosi d_{i} + V(k + 1, i + 1).
Ako se donese odluka A_{2}, tj. odluči li se zamijeniti oprema, u godini k pojavit će se trošak nabave nove opreme i neto dobit nastala korištenjem nove opreme. Trošak nabave nove opreme jednak je nabavnoj cijeni opreme, tj. p. Godišnja neto dobit nastala korištenjem nove opreme iznosi d_{0}. Stoga ukupna neto dobit u godini k iznosi d_{0} - p. Sljedeća etapa u kojoj se donosi odluka je početak (k + 1) godine, a u tom trenutku raspolaže se opremom starom jednu godinu. Najveća ukupna neto dobit od početka (k + 1) godine do kraja razdoblja planiranja, prema definiciji funkcije V, iznosi V(k + 1, 1). Prema tome, ukupna neto dobit nastala kao posljedica izbora alternative A_{2} na početku godine k iznosi d_{0} - p + V(k + 1, 1).
Budući da ukupnu neto dobit treba maksimizirati u svakoj pojedinoj etapi, iz navedenih razmatranja proizlazi sljedeća jednakost:
\begin{align*}V(k,i) &= \max \big\lbrace d_{i} + V(k + 1, i + 1), \ d_{0} - p + V(k + 1, 1) \big\rbrace \\ &= \max \big\lbrace d_{i} + V(k + 1, i + 1), \ 120 - 120 + V(k + 1, 1) \big\rbrace \\ &= \max \big\lbrace d_{i} + V(k + 1, i + 1), \ V(k + 1, 1) \big\rbrace \text{.}\end{align*}
Preostaje zadati početne uvjete. U tu se svrhu razmatra odluka koja se donosi početkom posljednje godine razdoblja planiranja, odnosno početkom osme godine. Pripadna vrijednost varijable etape je k = 8, pa se zapravo zadaju vrijednosti V(8, i). Najmanja moguća vrijednost varijable stanja je i_{\min} = 0 i postiže se ako se početkom 8. godine donese odluka o kupnji nove opreme. Najveća moguća vrijednost varijable stanja jednaka je i_{\max} = 3 + 7 = 10 i postiže se ako se oprema stara 3 godine zadrži tijekom svih osam godina. Budući da, prema definiciji funkcije V, za svaki k = 9, 10, 11, \ldots i svaki i \in \mathbb{N} vrijedi jednakost:
V(k,i)=0 ,
izraz za izračunavanje vrijednosti V(8, i) može se transformirati ovako:
\begin{align*}V(8, i) &= \max \big\lbrace d_{i} + V(8 + 1, i + 1), \ d_{0} - p + V(8 + 1, 1) \big\rbrace \\ &= \max \big\lbrace d_{i} + V(9, i + 1), \ 120 - 120 + V(9, 1) \big\rbrace \\ &= \max \big\lbrace d_{i} + 0, \ 0 \big\rbrace = d_{i} \text{.}\end{align*}
Dobiva se:
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| V(8,i) | 120 | 100 | 80 | 60 | 40 | 20 | 0 | 0 | 0 | 0 | 0 |
U sljedećoj fazi računaju se vrijednosti V(7, i). U etapi k = 7, tj. početkom 7. godine najveća moguća vrijednost varijable stanja je i_{\max} = 3 + 6 = 9, pa se računaju vrijednosti V(7, i) za i = 0, 1, 2, \ldots, 8, 9. Koristeći se navedenom dvoindeksnom rekurzivnom relacijom, dobiva se:
\begin{align*} V(7, 0) &= \max \big\lbrace d_{0} + V(7 + 1, 0 + 1), \ V(7 + 1, 1) \big\rbrace \\ &= \max \big\lbrace 120 + V(8, 1), \ V(8, 1) \big\rbrace = \max \big\lbrace 120 + 100, \ 100 \big\rbrace = 220 ; \\ V(7, 1) &= \max \big\lbrace d_{1} + V(7 + 1, 1 + 1), \ V(7 + 1, 1) \big\rbrace \\ &= \max \big\lbrace 100 + V(8, 2), \ V(8, 1) \big\rbrace = \max \big\lbrace 100 + 80, \ 100 \big\rbrace = 180 ; \\ V(7, 2) &= \max \big\lbrace d_{2} + V(7 + 1, 2 + 1), \ V(7 + 1, 1) \big\rbrace \\ &= \max \big\lbrace 80 + V(8, 3), \ V(8, 1) \big\rbrace = \max \big\lbrace 80 + 60, \ 100 \big\rbrace = 140 ; \\ V(7, 3) &= \max \big\lbrace d_{3} + V(7 + 1, 3 + 1), \ V(7 + 1, 1) \big\rbrace \\ &= \max \big\lbrace 60 + V(8, 4), \ V(8, 1) \big\rbrace = \max \big\lbrace 60 + 40, \ 100 \big\rbrace = 100 ; \\ V(7, 4) &= V(7, 5) = V(7, 6) = V(7, 7) = V(7, 8) = V(7, 9) = V(8, 1) = 100 \end{align*}
(što znači da ako se početkom sedme godine raspolaže opremom starom barem 3 godine, svakako se isplati kupiti novu).
Analogno se postupa u svakoj od sljedećih šest faza. Dobivaju se sljedeće vrijednosti:
\begin{align*} V(6,0) & = 300, \ V(6,1) = 240, \ V(6,2) = 180, \\ V(6,3) & = V(6,4) = V(6,5) = V(6,6) = V(6,7) = V(6,8) = 180 \end{align*}
(što znači da ako se početkom šeste godine raspolaže opremom starom barem dvije godine, svakako se isplati kupiti novu);
\begin{align*} V(5,0) & = 360, \ V(5,1) = 280, \ V(5,2) = 260, \ V(5,3) = 240, \\ V(5,4) & = V(5,5) = V(5,6) = V(5,7) = 240 \end{align*}
(što znači da ako se početkom pete godine raspolaže opremom starom barem tri godine, svakako se isplati kupiti novu);
\begin{align*} V(4,0) & = 400, \ V(4,1) = 360, \ V(4,2) = 320, \ V(4,3) = 300, \ V(4,4) = 280, \\ V(4,5) &= V(4,6) = 280 \end{align*}
(što znači da ako se početkom četvrte godine raspolaže opremom starom barem četiri godine, svakako se isplati kupiti novu);
\begin{align*} V(3,0) & = 480, \ V(3,1) = 420, \ V(3,2) = 380, \ V(3,3) = 360, \\ V(3,4) &= V(3,5) = 360 \end{align*}
(što znači da ako se početkom treće godine raspolaže opremom starom barem tri godine, svakako se isplati kupiti novu);
V(2,0) = 540, \ V(2,1) = 480, \ V(2,2) = 440, \ V(2,3) = 420, \ V(2,4) = 420
(što znači da ako se početkom druge godine raspolaže opremom starom barem tri godine, svakako se isplati kupiti novu);
V(1,0) = 600, \ V(1,1) = 540, \ V(1,2) = 500, \ V(1,3) = 480\text{.}
Prema tome, tražena maksimalna ukupna neto dobit u cjelokupnom razdoblju planiranja iznosi 480 n.j. Preostaje odrediti optimalnu politiku zamjene opreme, odnosno «očitati» slijed odluka. Vrijednost V(1, 3) = 480 postiže se neovisno o izboru alternative (A_{1} ili A_{2}). Stoga se dobivaju sljedeće optimalne politike:
1. optimalna politika
| \bullet | početak 1. godine: zadržati postojeću opremu; |
| \bullet | početak 2. godine: zamjena opreme; |
| \bullet | početak 3., početak 4. i početak 5. godine: zadržati postojeću opremu; |
| \bullet | početak 6. godine: zamjena opreme; |
| \bullet | početak 7. i početak 8. godine: zadržati postojeću opremu. |
| \bullet | početak 1. godine: zadržati postojeću opremu; |
| \bullet | početak 2. godine: zamjena opreme; |
| \bullet | početak 3. i početak 4. godine: zadržati postojeću opremu; |
| \bullet | početak 5. godine: zamjena opreme; |
| \bullet | početak 6., početak 7. i početak 8. godine: zadržati postojeću opremu. |
| \bullet | početak 1. godine: zamjena opreme; |
| \bullet | početak 2., početak 3. i početak 4. godine: zadržati postojeću opremu; |
| \bullet | početak 5. godine: zamjena opreme; |
| \bullet | početak 6., početak 7. i početak 8. godine: zadržati postojeću opremu. |
Ako se unaprijed donese odluka da se na početku prve godine zamjenjuje dotad korištena oprema, postupak donošenja optimalne politike zamjene može se svesti na određivanje kritičnoga puta u težinskom digrafu. Navedeno je modeliranje moguće ako i samo ako je težina svakoga luka (i, j) za i \lt j pozitivan realan broj4. Postupak se prikazuje na sljedećem primjeru.
Primjer 5
Treba riješiti primjer
Matematički model je potpuni težinski digraf čiji vrhovi označuju početke godina. Budući da je razdoblje planiranja dugo n = 8 godina, digraf će imati ukupno n + 1 = 8 + 1 = 9 vrhova: 1, 2, 3, 4, 5, 6, 7, 8, 9 (vrh 9 interpretiramo kao kraj 8. godine, odnosno kraj razdoblja planiranja). Vrhovi i i j bit će spojeni lukom od i prema j ako i samo ako je i \lt j, pa će graf imati ukupno \binom{9}{2} = 36 različitih lukova. Preostaje zadati težinu svakoga luka:
\begin{split} w_{ij} & = \text{(ukupna neto dobit nastala korištenjem opreme u godinama} \\ & \qquad \text{}i\text{, }i + 1\text{, }\ldots\text{, }j - 2\text{, }j - 1\text{)} - \text{(nabavna cijena opreme u godini }i\text{)} \\ & = \sum_{k=0}^{j-i-1}d_{k} - p_{i} . \end{split}
Budući da je d_{0} = p = 120 n.j, ukupna neto dobit u prvoj godini korištenja opreme jednaka je 0, pa za svaki i = 1, 2, 3, 4, 5, 6, 7, 8 vrijede jednakosti:
\begin{gather*} w_{i,i+1} = 0 , \\ w_{i,i+k} = \sum_{m=1}^{k-1}d_{k} , \ \text{ za svaki }k \in \mathbb{N} \setminus \lbrace 1\rbrace \text{ za koji postoji luk }(i,i+k)\text{.} \end{gather*}
Prema definiciji veličina d_{i}, za svaki i \in \mathbb{N} očito vrijedi nejednakost d_{i} \geq 0, pa je nužan uvjet za modeliranje problema potpunim težinskim digrafom ispunjen. Nadalje, zbog
\begin{align*} d_{1} & = 120 - 20 \cdot 1 = 100 ; & d_{5} & = 120 - 20 \cdot 5 = 20 ; \\ d_{2} & = 120 - 20 \cdot 2 = 80 ; & d_{6} & = 120 - 20 \cdot 6 = 0 ; \\ d_{3} & = 120 - 20 \cdot 3 = 60 ; & d_{7} & = 0 ; \\ d_{4} & = 120 - 20 \cdot 4 = 40 ; & d_{8} & = 0 , \end{align*}
slijedi:
\begin{align*} w_{12} & = w_{23} = w_{34} = w_{45} = w_{56} = w_{67} = w_{78} = w_{89} = 0 ; \\ w_{13} & = w_{24} = w_{35} = w_{46} = w_{57} = w_{68} = w_{79} = d_{1} = 100 ; \\ w_{14} & = w_{25} = w_{36} = w_{47} = w_{58} = w_{69} = d_{1} + d_{2} = 100 + 80 = 180 ; \\ w_{15} & = w_{26} = w_{37} = w_{48} = w_{59} = d_{1} + d_{2} + d_{3} = 100 + 80 + 60 = 240 ; \\ w_{16} & = w_{27} = w_{38} = w_{49} = d_{1} + d_{2} + d_{3} + d_{4} = 100 + 80 + 60 + 40 = 280 ; \\ w_{17} & = w_{28} = w_{39} = d_{1} + d_{2} + d_{3} + d_{4} + d_{5} = 100 + 80 + 60 + 40 + 20 = 300 ; \\ w_{18} & = w_{29} = d_{1} + d_{2} + d_{3} + d_{4} + d_{5} + d_{6} = 100 + 80 + 60 + 40 + 20 + 0 = 300 ; \\ w_{19} & = d_{1} + d_{2} + d_{3} + d_{4} + d_{5} + d_{6} +d_{7} = 100 + 80 + 60 + 40 + 20 + 0 + 0 = \\ & = 300 \text{.} \end{align*}
Uz pomoć računalnoga programa Grin dobiva se digraf prikazan na slici
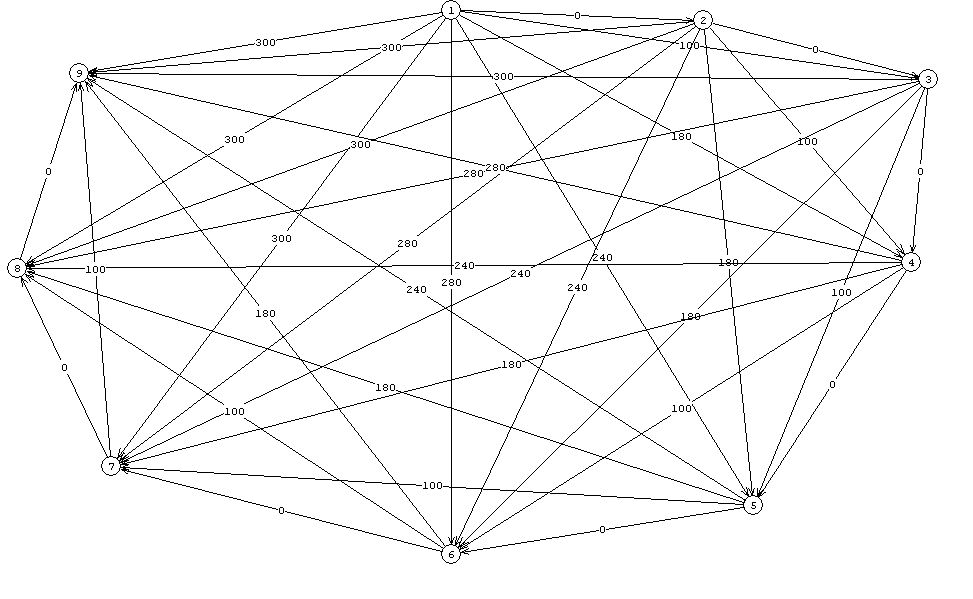
Slika 3:
Model problema iz primjera 5 .
Primjenom procedure Critical Path implementirane u istom računalnom programu određuje se kritični put u tom digrafu:
1 — 5 — 9.
Njegova je težina 480 i ona je jednaka optimalnoj ukupnoj neto dobiti. Jedini unutrašnji vrh u kritičnom putu je vrh 5, pa slijedi da početkom 5. godine treba zamijeniti dotadašnju opremu. Kad se tomu doda unaprijed postavljeni uvjet da se početkom prve godine obavezno kupuje nova oprema, dobiva se 3. optimalna politika dobivena u rješenju primjera
Zaključno se može istaknuti kako se još neki tipovi logističkih problema također mogu riješiti uz pomoć modela i algoritama teorije grafova (vidjeti
Bibliografija
| [1] | Schun–Chen Niu, Dynamic Programming, School of Management, University of Texas, Dallas, http://www.utdallas.edu/ scniu/OPRE-6201/documents/DP2-Equipment-Replacement.pdf, 15. 6. 2009. |
| [2] | Farid AitSahlia, Operations Research 2, Industrial and Systems Engineering, University of Florida, Weil Hall, http://www.ise.ufl.edu/esi4313/DP.ppt, 15. 6. 2009. |
| [3] | Michael Trick, Dynamic Programming, Tepper School of Business, Carnegie Mellon University, Pittsburg, http://mat.gsia.cmu.edu/classes/dynamic/node7.html, 15. 6. 2009. |
| [4] | Maja Fošner, Tomaž Kramberger, Teorija grafova i logistika, math.e, broj 14, http://e.math.hr/math_e_article/br14/fosner_kramberger, Zagreb, 2009. |
| [5] | Richard E. Bellman, Dynamic Programming, Courier Dover Publication, 2003. |
| [6] | Blaženka Divjak, Alen Lovrenčić, Diskretna matematika s teorijom grafova, FOI – TIVA, Varaždin, 2005. |
| [7] | Jovan Petrić, Operaciona istraživanja, Nauka, Beograd, 1997. |
| [8] | Jovan Petrić, Lazar Šarenac, Zdravko Kojić, Operaciona istraživanja – zbirka rešenih zadataka, Nauka, Beograd, 1996. |
1Radi jednostavnosti, pretpostavlja se da su u navedenu cijenu uračunati svi pripadajući porezi, prirezi itd. n.j. je pokrata za novčanu jedinicu.
2Likvidacijska vrijednost nekoga sredstva je vrijednost rashodovanoga stalnog sredstva koja se dobije tako da se od tržišne cijene toga sredstva odbiju troškovi rashodovanja.
3Godišnji trošak održavanja automobila staroga točno 5 godina jednak je nuli. Naime, ako je početkom neke godine godine starost automobila točno 5 godina, obavezno odmah rashodujemo automobil kako bismo izbjegli daljnje troškove njegova održavanja.
4Ako je težina luka (i,j) negativan realan broj, luk (i,j) treba zamijeniti lukom (j,i) čija je težina pozitivan realan broj. Navedena zamjena može dovesti do nastanka ciklusa u grafu (osobito ako je graf potpun), a u takvim slučajevima traženi kritični put ne postoji.