Od koenigsberških mostova do kineskog poštara
2012
Od koenigsberških mostova do kineskog poštara
Sažetak
U članku se daje kratak osvrt na povijest teorije grafova i u tom kontekstu govori o rješavanju Problema kineskog poštara kao jednog o najpoznatijih problema kombinatorne optimizacije.
1Što bilježe kroničari
Teorija grafova ima dosta precizne povijesne odrednice. Prvi rad iz teorije grafova je Eulerovo1 rješenje pitanja šetnje koenigsberškim mostovima, objavljen 1736. godine,
U 60-tim godinama dvadesetog stoljeća počinje snažan razvoj istraživanja u teoriji grafova i njenim primjenama koji traje do danas. U razdoblju od 1960. do 1970. broj godišnje objavljenih radova se više nego udeseterostručio. Danas imamo na desetke uglednih časopisa koji gotovo isključivo objavljuju članke iz teorije grafova i njenih primjena. Neobično intenzivan razvoj i veliku popularnost teorija grafova je doživjela zahvaljujući, izravno ili neizravno, naglom razvoju modernih informacijskih tehnologija. Jasna geometrijska predodžba koju graf sadržiava i koja je bliska intuitivnom poimanju osobina i veza objekata predstavljenih grafom pridonijela je širokom spektru primjene grafova. S druge strane, grafovi postaju univerzalni matematički jezik kojim je moguće opisati najrazličitije, i sasvim apstraktne matematičke strukture.
Ovdje ćemo usmjeriti pozornost na dvije slavne teme: šetnje koenigsberškim mostovima i problem kineskog poštara.
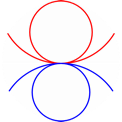
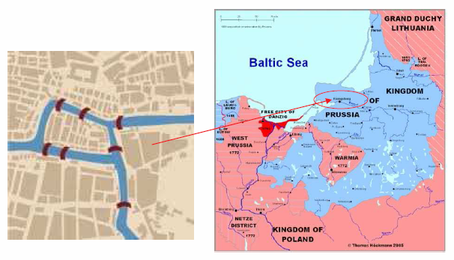
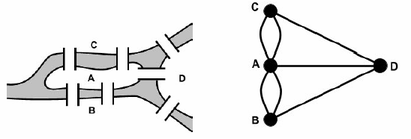
Građani Koenigsberga (tada glavni grad pruskog kraljevstva, a poslije Kalinjingrad u Rusiji) zabavljali su se starim pitanjem mogu li prošetati svojim gradom tako da svaki od 7 mostova na rijeci Pregel pređu točno jedanput i završe šetnju u polaznoj točki, Slika
Početkom 60-tih godina dvadesetog stoljeća kineski matematičar M. Guan (Meigu Guan ili Mei-Ko Kwan) postavlja i proučava pitanje optimizacije poštarova puta pri dostavi pošiljki,
2Malo o grafovima
Definicija 1. Graf je uređena trojka G=(V,E,\varphi), gdje je V=V\left( G\right) neprazan skup čije elemente nazivamo vrhovima, E=E\left( G\right) je skup disjunktan s V čije elemente nazivamo bridovima i \varphi je funkcija koja svakom bridu e iz E pridružuje par \left\lbrace u,v\right\rbrace, ne nužno različitih vrhova iz V. Graf skraćeno označavamo G=(V,E) ili samo G.
Vrhove u i v koji su pridruženi bridu e nazivamo krajevima brida e. Brid čiji se krajevi podudaraju nazivamo petljom. Višestruki bridovi su dva ili više njih s istim parom krajeva. Za par vrhova u i v kažemo da su susjedni ako postoji brid e kojemu su oni krajevi. Pri tome kažemo da je brid e incidentan s vrhovima u i v, za što ćemo upotrijebiti oznaku e=\left\lbrace u,v\right\rbrace ili e=uv. Stupanj vrha v u grafu G je broj bridova grafa G incidentnih s v, pri čemu se svaka petlja računa kao dva brida. Izolirani vrh je vrh stupnja 0.
Šetnja u grafu G je niz W:=v_{0}e_{1}v_{1}e_{2}...e_{k}v_{k} čiji članovi su naizmjenično vrhovi v_{i} i bridovi e_{i}, tako da su krajevi od e_{i} vrhovi v_{i-1} i v_{i}, i=1,\ldots,k. Kažemo da je v_{0} početak a v_{k} kraj šetnje W, da je W šetnja od v_{0} do v_{k} ili \left( v_{0},v_{k}\right)-šetnja. Šetnja se, kada to ne umanjuje jasnoću, skraćeno zapisuje samo bridovima W=e_{1}e_{2}...e_{k}. Šetnja je zatvorena ako se početak i kraj podudaraju, tj. ako je v_{0}=v_{k}. Šetnju kojoj su svi bridovi međusobno različiti nazivamo stazom. Put je staza čiji su vrhovi međusobno različiti. Dva vrha u i v grafa G su povezana ako postoji \left( u,v\right)-put u G. Graf je povezan ako su svaka dva njegova vrha povezana.
Eulerova staza je staza koja sadržava svaki brid grafa (točno jedanput!). Eulerova tura u grafu je zatvorena Eulerova staza. Ako graf dopušta Eulerovu turu kažemo da je Eulerov graf.
Odgovor na pitanje koji graf ima Eulerovu turu ili Eulerovu stazu daje sljedeći karakterizacijski teorem.
Teorem 2. Povezani graf je Eulerov ako i samo ako mu je svaki vrh parnog stupnja. Povezani graf koji nije Eulerov sadržava Eulerovu stazu ako i samo ako ima točno dva vrha neparnog stupnja.
Graf sa Slike
Rješavajući probleme "obilazaka gradskih ulica" nerijetko treba uzeti u obzir dodatni parametrar kao što je "dopušteni smjer". Traženje matematičkog modela za slične probleme prirodno vodi pojmu usmjerenog grafa.
Definicija 3. Digraf ili usmjereni graf D je uređena trojka D=\left( V,A,\psi\right), gdje je V=V\left( D\right) neprazan skup čije elemente nazivamo vrhovima, A=A\left( D\right) skup disjunktan s V čije elemente nazivamo lukovima i \psi funkcija koja svakom luku a iz A pridružuje uređeni par (u,v), pri čemu u,v\in V nisu nužno različiti. Kažemo da je u početak, a v kraj luka a, da je smjer ili orijentacija luka a od u prema v i koristimo oznaku a=(u,v). Digraf skraćeno označavamo D\left( V,A\right) ili samo D.
Pojmove koje smo imali kod grafova analogno definiramo za digrafove. Dva ili više lukova s istim početkom i krajem su višestruki lukovi. Usmjerena šetnja u digrafu D je niz W:=v_{0} e_{1}v_{1}e_{2}...e_{k}v_{k} čiji članovi su naizmjenično vrhovi v_{i} i lukovi e_{i} tako da je početak od e_{i} vrh v_{i-1}, a kraj mu je v_{i}, i=1,\ldots,k. Kažemo da je v_{0} početak, a v_{k} kraj usmjerene šetnje W ili da je W\left( v_{0} ,v_{k}\right) usmjerena šetnja. Usmjerena šetnja je zatvorena ako je v_{0}=v_{k}. Usmjerenu šetnju kojoj su svi lukovi međusobno različiti nazivamo usmjerenom stazom. Usmjereni put je usmjerena staza čiji su vrhovi međusobno različiti. Usmjerena Eulerova tura je usmjerena zatvorena staza koja svaki luk digrafa sadržava točno jedanput. Eulerov digraf je onaj koji ima Eulerovu turu.
Pripadajući graf G\left( D\right) digrafa D je graf dobiven zamjenom svakog luka a=\left( u,v\right) bridom e=\left\lbrace u,v\right\rbrace. Digraf D je slabo povezan (kraće povezan) ako je pripadajući graf povezan, a jako povezan ako za svaka dva vrha u,v\in V\left( D\right) postoje \left( u,v\right) i \left( v,u\right) usmjereni putovi. Ulazni (izlazni) stupanj vrha v digrafa je broj lukova kojima je v kraj (početak).
Eulerov digraf ima karakterizaciju analognu onoj koju za Eulerov graf daje Teorem
Teorem 4. Povezani digraf je Eulerov ako i samo ako je za svaki njegov vrh ulazni stupanj jednak izlaznom.
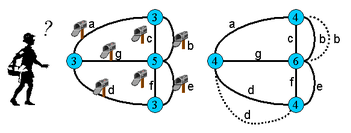
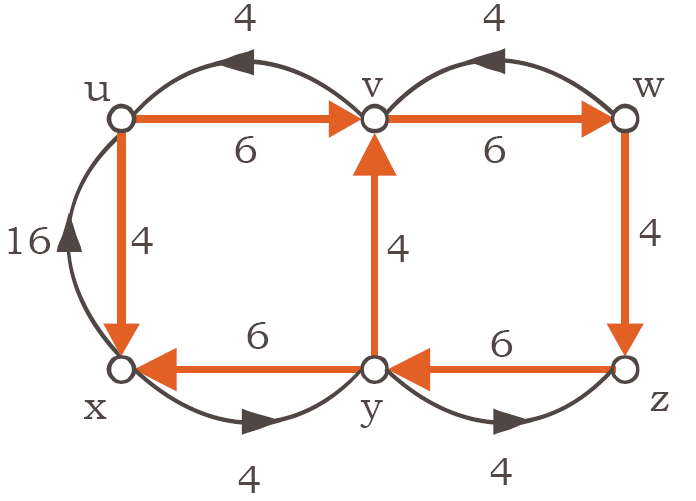
Smjer luka na skicama označavamo strelicom koja pokazuje od početka prema kraju luka. Jedan digraf prikazan je na Slici
Opširnije o spomenutim pojmovima i tvrdnjama može se naći u brojnim knjigama iz teorije grafova kao što su
3Traženje rješenja za CPP
Vratimo se Problemu kineskog poštara na primjeru grafa za koenigsberške mostove, Slika
Pri traženju najkraćeg poštarovog obilaska gradskih ulica treba uzeti u obzir parametre kao što su duljine ulica ili vrijeme potrebno za prolazak tim ulicama. Matematički model za ovaj i slične probleme je težinski graf.
Definicija 5. Težinski graf je uređeni par \left( G,\omega\right), gdje je G graf i \omega:E\left( G\right) \rightarrow \mathbb{R} _{0}^{+} funkcija koja svakom bridu e iz G pridružuje nenegativni broj \omega\left( e\right). Vrijednost\ \omega\left( e\right) nazivamo težinom brida e.
Težine bridova težinskog grafa mogu predstavljati udaljenost, vrijeme, visinu nekih troškova i slično.
Definicija 6. Poštarova tura u grafu G je zatvorena šetnja koja uključuje svaki brid grafa G najmanje jednom. U težinskom grafu optimalna poštarova tura je poštarova tura kojoj je ukupna težina uključenih bridova minimalna.
Dakle, osnovnmi oblik CPP-a svodi sena traženje optimalne poštarove ture u težinskom grafu. Ako je graf Eulerov, svaka Eulerova tura je optimalna poštarova tura pa je njenim pronalaskom problem riješen. Navest ćemo dva standardna algoritma za pronalaženje Eulerove ture, Fleuryjev i Hierholzerov. Pri tome ćemo se koristiti nekim pojmovima i oznakama iz teorije grafova koje do sada nismo spomenuli pa ih ovdje uvodimo.
Ako su G i H grafovi, V\left( H\right) \subseteq V\left( G\right), E\left( H\right) \subseteq E\left( G\right) i svaki brid iz H ima iste krajeve u H kao što ih ima u G, onda kažemo da je H podgraf od G. Neka je G=\left( V,E\right) i E^{\prime }\subseteq E. Podgraf od G čiji je skup vrhova V i skup bridova E\setminus E^{\prime} označavamo G-E. Ako je E^{\prime}=\left\lbrace e\right\rbrace, koristimo oznaku G-e. Komponenta povezanosti grafa G je maksimalni povezani podgraf od G, tj. povezani podgraf koji nije sadržan ni u jednom drugom povezanom podgrafu. Za broj komponenti povezanosti grafa G koristimo se oznakom c\left( G\right). Rezni brid u grafu G je brid e\in E\left( G\right) za koji je c\left( G-e\right) \gt c\left( G\right), tj. čijim se izostavljanjem povećava broj komponenti povezanosti.
-
- Algoritam 1.
- Fleuryjev algoritam
Ulaz: Eulerov graf G.
Izlaz: Eulerova tura C u grafu G.
Korak 1: Izabrati proizvoljni vrh v\in V(G). Postaviti v za tekući vrh i C:=v.
Korak 2: Označiti proizvoljni brid e koji je incidentan s tekućim vrhom i nije rezni brid te ga dodati stazi C. Samo ako nema drugih mogućnosti, za e uzeti rezni brid. Postaviti za tekući vrh drugi kraj brida e.
Korak 3: Izbrisati označeni brid iz G. Ako nema preostalih bridova: KRAJ; u suprotnom: povratak na Korak 2.
Hierholzerov algoritam traži Eulerovu turu u Eulerovom grafu bez provjere je li brid kojim prolazi rezni. Ovaj algoritam konstruira u grafu sukcesivno zatvorene staze čijim se spajanjem u konačnici dobije Eulerova tura.
-
- Algoritam 2.
- Hierholzerov algoritam
Ulaz: Eulerov graf G.
Izlaz: Eulerova tura u grafu G.
Korak 1: Izabrati proizvoljni vrh v\in V(G).
Korak 2: Konstruirati zatvorenu stazu C_{0} u G s početkom u vrhu v. Postaviti\ i:=0.
Korak 3: Ako je E\left( C_{i}\right) =E\left( G\right) (C_{i} Eulerova tura u G): KRAJ.
Ako je E\left( C_{i}\right) \neq E\left( G\right) , odabrati vrh v_{i}\in C_{i} incidentan bridu e\notin C_{i} i konstruirati zatvorenu stazu C_{i}^{\ast} u grafu G-E\left( C_{i}\right) s početkom u vrhu v_{i}.
Korak 4: Spajanjem staza C_{i} i C_{i}^{\ast} konstruirati zatvorenu stazu C_{i+1} s početkom u vrhu v_{i-1}\in C_{i}; ići stazom C_{i} do v_{i}\in C_{i}, zatim preko svih bridova u C_{i}^{\ast} i potom svih preostalih bridova u C_{i}. Postaviti i:=i+1 i ići na Korak 3.
Ako graf nije Eulerov, dodavanjem ponovljenih bridova može se prevesti u graf koji ima Eulerovu turu, što je bila Guanova polazna ideja,
4Varijacije problema
Kao što je rečeno, osnovni oblik CPP-a svodi se na traženje optimalne poštarove ture u težinskom grafu. Pokazalo se da uz određene modifikacije ovaj model može postati način rješavanja velikog broja vrlo različitih optimizacijskih problema, o čemu govore brojne publikacije. Spomenut ćemo za ilustraciju
Primjer 7. Poznati primjer primjene CPP-a je optimizacija rute za čišćenje ulica grada New Yorka, [2, 3] . Pretpostavimo da usmjereni graf na Slici 4 predstavlja mrežu jednosmjernih ulica. Težine lukova znače vrijeme potrebno za prolazak ulicom bez čišćenja. Lukovi su bojenjem podijeljeni u dvije klase; jedna boja (crvena) označava ulice koje treba očistiti, a druga ulice koje se mogu koristiti za prolazak. Zadatak je odrediti koja ruta minimizira ukupno vrijeme potrebno za čišćenje zadanih ulica, na način da se krene iz vrha z i završi u vrhu z.
Za primjer smo mogli uzeti slučaj u kojemu se pojavljuju i jednosmjerne i dvosmjerne ulice. To upućuje na model koji će istovremeno imati bridove i lukove.
Definicija 8. Mješoviti graf je uređena trojka M=\left( V,E,A\right), gdje je V skup vrhova, E skup bridova i A skup lukova.
S vremenom su, kroz primjene, nastale brojne verzije CPP-a vezane uz različite optimizacijske probleme. Glavne verzije su određene tipom modela. Neusmjereni CPP (UCPP-Undirected Chinese Postman Problem) za model ima težinski graf, usmjereni CPP (DCPP-Directed Chinese Postman Problem) modelira se u digraf, kao u Primjeru
Problem ruralnog poštara (CRPP-Rural Postman Problem) je varijacija UCPP-a u kojoj se razmatra povezani težinski graf G=\left( V,E\right) s podskupom E^{\prime}\subseteq E istaknutih bridova. Cilj je pronaći zatvorenu šetnju u G najmanje težine koja svaki brid e\in E^{\prime} prijeđe barem jednom. Ime problema dolazi iz prakse dostave pošte u ruralnim sredinama gdje postoje ulice u kojima nijedan stanovnik tog dana nema pošte, ali te ulice ipak mogu služiti kao poveznice među ulicama u koje tog dana treba dostaviti poštu.
Vjetroviti CPP (WPP-Windy Postman Problem) razmatra povezani težinski graf G=\left( V,E\right) sa zadanim dvjema težinskim funkcijama. Težine svakog pojedinog brida mogu se razlikovati ovisno o smjeru prelaska brida ("s vjetrom u leđa" ili "protiv vjetra"). Cilj je pronaći zatvorenu šetnju u G najmanje težine koja svaki brid e\in E sadržava barem jedanput.
Generalizirani CPP (GCPP-Generalized Chinese Postman Problem) modelira se u povezani težinski graf G=\left( V,E\right) čiji je skup bridova E podijeljen u podskupove E_{1},...,E_{k}. Potrebno je pronaći zatvorenu šetnju najmanje težine koja sadržava barem jedan brid iz svakog od podskupova E_{1},...,E_{k}.
Mješoviti k-CPP (M k-CPP-Mixed k-Chinese Postman Problem) polazi od jako povezanog mješovitog težinskog grafa G=\left( V,E,A\right) s istaknutim vrhom i zadanim brojem k\gt 1. Cilj je pronaći skup od k mješovitih zatvorenih šetnji minimalne ukupne težine koje zadovoljavaju sljedeće uvjete:
(a) svaka šetnja počinje i završava u istaknutom vrhu;
(b) svaki brid sadržan je u barem jednoj šetnji.
Min-max k-CPP (MM k-CPP-Min-Max k-Chinese Postman Problem) kao polazište ima povezani težinski graf G=\left( V,E\right) s istaknutim vrhom i zadanim brojem k\gt 1. Promatraju se svi skupovi od k zatvorenih šetnji koje zadovoljavaju uvjete (a) i (b). Među njima treba pronaći skup koji ima minimalnu težinu najteže šetnje.
Hijerarhijski CPP (HCPP-Hierarchical Chinese Postman Problem) razmatra povezan težinski graf G=\left( V,E\right) čiji je skup bridova E podijeljen u nekoliko klasa između kojih je uspostavljen odnos prednosti. Ako klasa E_{p} ima veću prednost od klase E_{q}, onda bridovi iz E_{p} moraju biti prijeđeni prije onih iz E_{q}. U tom grafu treba pronaći zatvorenu šetnju minimalne težine koja prelazi svaki brid barem jedanput, tako da se poštuje odnos prednosti klasa.
Primjenjivost CPP-a u praksi, uključujući i područja visoko komercijalnih modernih tehnologija, potiče potragu za učinkovitim algoritmima i programskim alatima za njegovo rješavanje
Napomena. Članak je nastao pri izradi završnog preddiplomskog rada Ane Mimice na studiju Matematike PMF-a u Splitu. Mrežne stranice korištene su kao izvornik za slike.
Bibliografija
