P	U	S	Č	P	S	N
						1
2	3	4	5	6	7	8
9	10	11	12	13	14	15
16	17	18	19	20	21	22
23	24	25	26	27	28	29
30

Pseudospektar matrica

linearna algebra

Ivica Nakić
PMF-Matematički odsjek
Sveučilište u Zagrebu
nakic@math.hr

Sažetak

Pojam svojstvenih vrijednosti i spektra matrice odavno se istražuje i koristi u matematici. Svojstvene vrijednosti matrica u mnogim slučajevima daju izvrstan uvid u svojstva samih matrica, no katkada ne daju dovoljno informacija za rješavanje problema na koje se može naići. Takvi se slučajevi pojavljuju u raznim granama matematike kao npr. teorije operatora i teorije Markovljevih lanaca i ostalih znanosti, od populacijske ekologije, preko laserske tehnologije, kvantne mehanike i hidrodinamike.

Katkada se preciznije informacije o matrici mogu dobiti korištenjem pseudospektra te je cilj ovog članka dati čitatelju osnovne informacije o ovom zanimljivom poopćenju pojma spektra.

U ovom će članku biti navedeni osnovni pojmovi vezani uz pseudospektar, ekvivalentne definicije pseudospektra, odnos prema običnom spektru matrica, kao i neka osnovna svojstva.

1Definicije pseudospektra

Promatrano u okvirima primijenjene matematike pitanje „Je li

$\textbf{A}$ singularna matrica?” često nema puno smisla. Naime, proizvoljno mala perturbacija matrice može promijeniti odgovor na to pitanje iz pozitivnog u negativan. Budući da se pitanje „Je li

$\lambda$ svojstvena vrijednost matrice

$\textbf{A}$ ?” može ekvivalentno postaviti u obliku „Je li

$\lambda-\textbf{A}$ singularna matrica?”, i ovdje nailazimo na isti problem.

Stoga je potrebno preformulirati ovo pitanje tako da uzmemo u obzir osjetljivost na perturbacije. Do pogodne formulacije dolazimo na osnovi sljedeće činjenice: što je matrica

$\textbf{A}$ bliža singularnoj matrici, to je matrica

$\textbf{A}^{-1}$ veća, u smislu da je norma te matrice veći broj.

Dakle, možemo postaviti pitanje „Je li

$\Vert \textbf{A}^{-1}\Vert$ velika?”.

Ako je odgovor da, onda je matrica jako blizu nekoj singularnoj matrici, te je za praktične svrhe možemo smatrati singularnom. Obrnuto, ako je odgovor ne, matrica će i uz male smetnje ostati regularnom.

Ako ovo rezoniranje primijenimo na problem svojstvenih vrijednosti, dolazimo do zaključka da bi od interesa mogli biti oni brojevi

$z$ za koje

$\Vert (z-\textbf{A})^{-1}\Vert$ ima veliku vrijednost.

Ovim slijedom razmišljanja dolazimo do prve definicije pseudospektra.

Definicija 1. (1. definicija pseudospektra) Neka je

$\textbf{A}\in\mathbb{C}^{N \times N}$ i

$\varepsilon\gt 0$ proizvoljan.

$\varepsilon$ -pseudospektar

$\sigma_{\varepsilon}(\textbf{A})$ matrice

$\textbf{A}$ u normi

$\Vert \cdot \Vert$ definiran je s

(1)

$\sigma_{\varepsilon} = \lbrace z \in \mathbb{C} : \Vert (z-\textbf{A})^{-1}\Vert \gt \varepsilon^{-1} \rbrace .$

Važno je uočiti da ova definicija ovisi o izboru norme

$\Vert \cdot \Vert$ , te se stoga katkada govoti o

$2$ –pseudospektru,

$1$ –pseudospektru i

$\infty$ –pseudospektru, ako je pripadna norma

$2$ –norma,

$1$ –norma, odnosno

$\infty$ –norma.

Mi ćemo se najčešće koristiti spektralnom

$2$ -normom u oznaci

$\Vert \cdot\Vert _{2}$ .

Matricu

$(z-\textbf{A})^{-1}$ zovemo rezolventom matrice

$\textbf{A}$ .

U (1), kao i u ostatku rada, podrazumijevamo da vrijedi:

(2)

$\Vert (z-\textbf{A})^{-1}\Vert =\infty \quad \text{za} \quad z\in\sigma(\textbf{A}),$

gdje

$\sigma(\textbf{A})$ predstavlja spektar matrice

$\textbf{A}$ .

Odavde slijedi da je

$\varepsilon$ -pseudospektar podskup kompleksne ravnine koji uvijek sadržava spektar pripadne matrice, i to za svaki

$\varepsilon\gt 0$ . Ako definiramo funkciju

$f(z):= \Vert (z-\textbf{A})^{-1} \Vert$ i iskoristimo činjenicu da je

$\Vert \cdot \Vert$ neprekidna funkcija, lako se zaključuje da je

$\varepsilon$ -pseudospektar otvoren skup kao praslika otvorenog skupa po neprekidnoj funkciji:

$\sigma_{\varepsilon}(\textbf{A})=f^{-1} ( \langle \varepsilon^{-1} , \infty ] ).$
Drugim riječima,

$\varepsilon$ -pseudospektar matrice otvoren je podskup kompleksne ravnine omeđen s

$\varepsilon^{-1}$ nivo krivuljom norme rezolvente matrice.

Intuitivno možemo pretpostaviti da je

$\Vert (z-\textbf{A})^{-1}\Vert$ velika upravo onda kada je točka

$z$ veoma blizu svojstvenoj vrijednosti matrice

$\textbf{A}$ . No, kao što ćemo poslije i demonstrirati, točnost naše intuicije ovisi o izboru matrične norme i normalnosti same matrice. Kod normalnih matrica, kada je

$\Vert \cdot\Vert =\Vert \cdot\Vert _{2}$ ,

$\Vert (z-\textbf{A})^{-1}\Vert$ velika točno onda kada je točka

$z$ blizu svojstvenoj vrijednosti matrice

$\textbf{A}$ (vidi Sliku 2). Važnost pseudospektra dolazi do izražaja kod matrica koje nemaju svojstvo normalnosti, a za koje norma

$\Vert (z-\textbf{A})^{-1}\Vert$ može biti velika čak i kada je točka

$z$ daleko od spektra matrice (vidi Sliku 2).

Neka je

$\textbf{A}$ matrica s potpunim skupom svojstvenih vektora

$\lbrace \textbf{v}_{j} \rbrace$ ,

$\textbf{V}$ neka je

$N \times N$ matrica čiji je

$j$ -ti stupac vektor

$\textbf{v}_{j}$ i

$\Lambda$ dijagonalna

$N \times \mathbb{N}$ matrica s

$j$ -tom svojstvenom vrijednošću

$\lambda_{j}$ na

$j$ -tom mjestu dijagonale. Znamo da tada matricu

$\textbf{A}$ možemo zapisati kao

$\textbf{A} = \textbf{V} \Lambda \textbf{V}^{-1}.$

$\varepsilon$ -pseudospektar će biti od važnosti kod matrica za koje je

(3)

$\Vert \textbf{V} \Vert \Vert \textbf{V}^{-1} \Vert \gg 1,$

uz odabranu normu

$\Vert \cdot \Vert$ .

Slika 1:

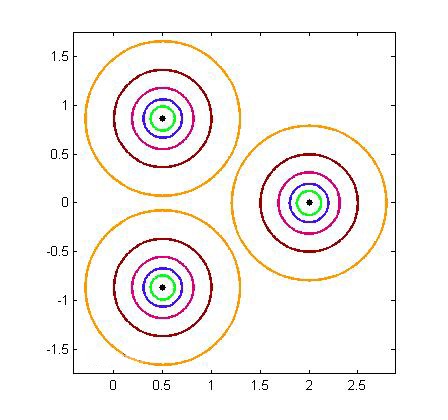
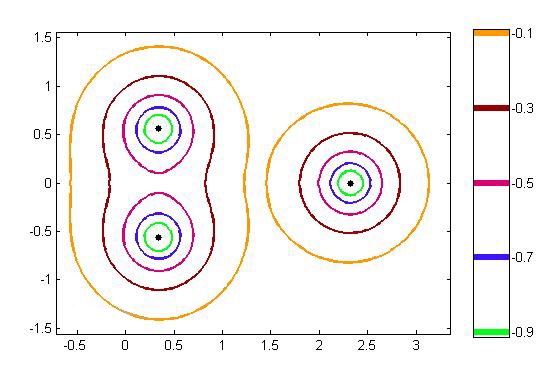
$\varepsilon$ -pseudospektar matrice u

$2$ -normi. Različito obojene linije predstavljaju granice pseudospektra za različite vrijednosti

$\varepsilon$ . Lijeva slika prikazuje pseudospektar normalne matrice, a desna pseudospektar matrice koja nema svojstvo normalnosti.

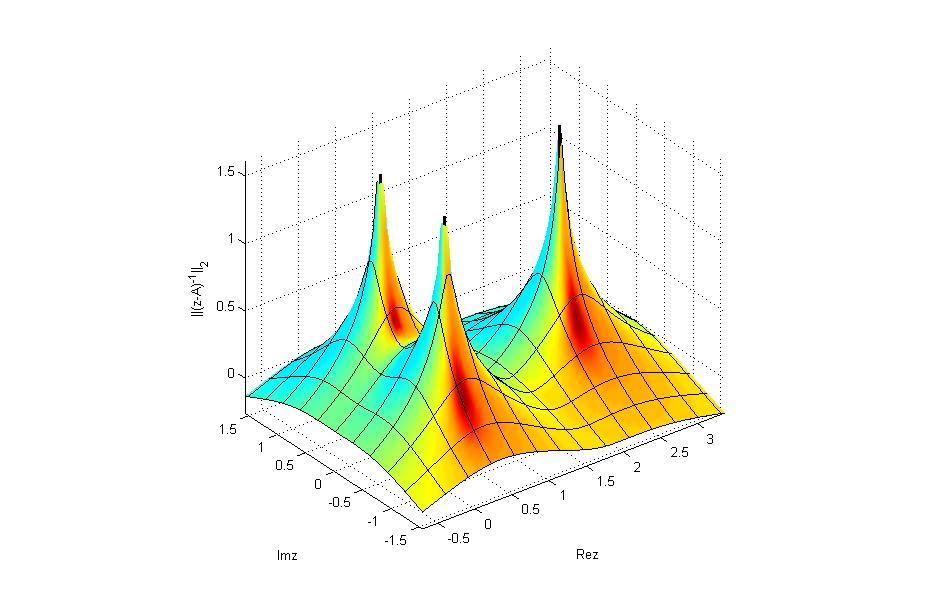
Slika 2: 3D prikaz pseudospektra matrice. Na

$z$ -osi nalazi se norma rezolvente matrice kao funkcija od

$z \in \mathbb{C}$ . Vidimo da je ona velika za brojeve blizu svojstvenim vrijednostima matrice.

Primijenimo li na matricu proizvoljno malu perturbaciju i tada gledamo spektar novodobivene matrice, dolazimo do alternativne definicije pseudospektra.

Definicija 2. (2. definicija pseudospektra)

$\sigma_{\varepsilon}(\textbf{A})$ u normi

$\Vert \cdot \Vert$ je skup svih

$z\in\mathbb{C}$ takvih da vrijedi

(4)

$z\in\sigma(\textbf{A}+\textbf{E})$

za neku matricu

$\textbf{E}\in\mathbb{C}^{N \times N}$ pri čemu je

$\Vert \textbf{E} \Vert \lt \varepsilon$ .

Drugim riječima,

$\varepsilon$ –pseudospektar je skup brojeva koji su svojstvene vrijednosti neke perturbirane matrice

$\textbf{A}+\textbf{E}$ gdje je

$\Vert \textbf{E} \Vert \lt \varepsilon$ .}

Iz ove definicije očito slijedi da za pseudospektre vezane uz raličite

$\varepsilon$ vrijedi

(5)

$\sigma_{\varepsilon_{1}}\subseteq\sigma_{\varepsilon_{2}}, \quad 0\lt \varepsilon_{1}\leq\varepsilon_{2},$

te također da je presjek svih mogućih pseudospektara matrice upravo spektar matrice

$\textbf{A}$ ,

(6)

$\bigcap_{\varepsilon\gt 0}\sigma_{\varepsilon}(\textbf{A})=\sigma(\textbf{A})$

Definicija 3. (3. definicija pseudospektra)

$\sigma_{\varepsilon}(\textbf{A})$ u normi

$\Vert \cdot \Vert$ je skup svih

$z\in\mathbb{C}$ t.d.

(7)

$\Vert (z-\textbf{A})\textbf{v}\Vert \lt \varepsilon$

za neki

$\textbf{v}\in\mathbb{C}^{N}$ pri čemu je

$\Vert \textbf{v}\Vert =1$ .

Broj

$z$ u (7) zovemo

$\varepsilon$ -pseudo svojstvena vrijednost matrice

$\textbf{A}$ , a

$\textbf{v}$ zovemo odgovarajući

$\varepsilon$ -pseudo svojstveni vektor. Drugim riječima,

$\varepsilon$ -pseudospektar je skup svih

$\varepsilon$ -pseudo svojstvenih vrijednosti.

Slika 3 prikazuje

$50 \times 50$ Basor-Morrisonovu matricu i ilustrira ekvivalenciju prve i treće definicije pseudospektra za matricu koja nije normalna. Na lijevoj slici vidimo granice

$\varepsilon$ -pseudospektra za različite

$\varepsilon$ , a na desnoj svojstvene vrijednosti

$100$ slučajno perturbiranih matrica. Očito je da su svojstvene vrijednosti matrice iznimno osjetljive na perturbacije, a ovaj primjer također lijepo prikazuje moguću geometrijsku strukturu matrica u kompleksnoj ravnini koja isprva nije vidljiva iz samog spektra matrice.

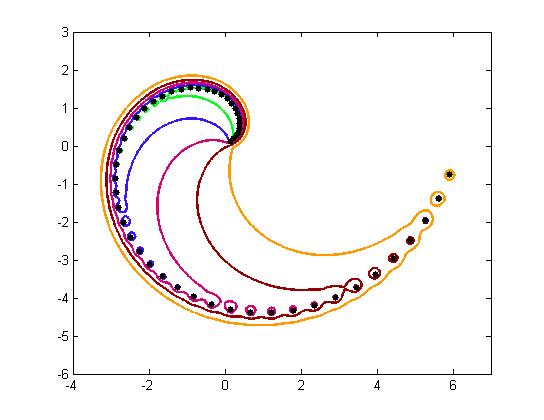
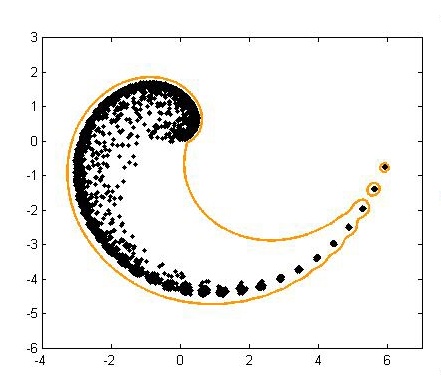
Slika 3: Pseudospektar

$50\times50$ Basor-Morrisonove matrice. Lijeva slika prikazuje svojstvene vrijednosti matrice (točke) i granice 2-norme

$\varepsilon$ -pseudospektra za

$\varepsilon=10^{-1},10^{-1.5},10^{-2},10^{-2.5},10^{-3}$ . Desna slika prikazuje pozicije svojstvenih vrijednosti

$100$ slučajno perturbiranih matrica

$\textbf{A+E}$ , gdje svaka matrica

$\textbf{E}$ ima nezavisne normalno distribuirane kompleksne vrijednosti i vrijedi

$\Vert \textbf{E}\Vert =10^{-1}$ . Kada bi u obzir bile uzete sve moguće perturbacije uz

$\Vert \textbf{E}\Vert \lt \varepsilon^{-1}$ , točke bi ispunile cijelo područje omeđeno najvećom granicom 2-norme s lijeve slike.

Slijedi teorem koji dokazuje da su ove tri definicije pseudospektra zaista ekvivalentne.

Teorem 4. (Ekvivalencija definicija pseudospektra) Tri gore navedene definicije pseudospektra su ekvivalentne za proizvoljnu matricu

$\textbf{A} \in \mathbb{C}^{N \times N}$ .

Dokaz. Ako je

$z\in\sigma(\textbf{A})$ ekvivalencija je očita, pa ćemo pretpostaviti da

$z\not \in \sigma(\textbf{A})$ , što povlači da

$(z-\textbf{A})^{-1}$ zaista postoji.

Da bismo dokazali (4)

$\Rightarrow$ (7), pretpostavimo da vrijedi

$(\textbf{A}+\textbf{E})\textbf{v}=z\textbf{v}$ za neki

$\textbf{E}\in\mathbb{C}^{N \times N}$ s

$\Vert \textbf{E}\Vert \lt \varepsilon$ i

$\textbf{v}\neq0$ ,

$\textbf{v}\in\mathbb{C}^{N}$ (možemo pretpostaviti da je vektor

$\textbf{v}$ normaliziran,

$\Vert \textbf{v}\Vert =1$ ). Tada vrijedi

$\Vert (z-\textbf{A})\textbf{v}\Vert =\Vert \textbf{E}\textbf{v}\Vert \lt \varepsilon,$ što je i trebalo dokazati.
Da bismo dokazali (7)

$\Rightarrow$ (1), pretpostavimo da vrijedi

$(z-\textbf{A})\textbf{v}=s\textbf{u}$ za neke

$\textbf{v},\textbf{u}\in\mathbb{C}^{N}$ takve da

$\Vert \textbf{v}\Vert =\Vert \textbf{u}\Vert =1$ i

$0\lt s\lt \varepsilon$ . Tada je

$(z-\textbf{A})^{-1}\textbf{u}=s^{-1}\textbf{v}$ te s jedne strane vrijedi

$\Vert (z - \textbf{A})^{-1} \textbf{u} \Vert \leq \Vert (z - \textbf{A})^{-1}\Vert \, \Vert \textbf{u} \Vert = \Vert (z - \textbf{A})^{-1}\Vert ,$ a s druge strane imamo

(8)

$\Vert (z - \textbf{A})^{-1} \textbf{u} \Vert =\Vert s^{-1} \textbf{v} \Vert = s^{-1}.$

Stoga

$\Vert (z - \textbf{A})^{-1}\Vert \geq s^{-1} \gt \varepsilon^{-1}.$
Da bismo dokazali (1)

$\Rightarrow$ (4), pretpostavimo da je

$\Vert (z-\textbf{A})^{-1}\Vert \gt \varepsilon^{-1}$ . Tada postoje

$\textbf{u,v} \in \mathbb{C}^{N}$ ,

$\Vert \textbf{u}\Vert =\Vert \textbf{v}\Vert =1$ i

$0\lt s\lt \varepsilon$ takvi da vrijedi

$(z - \textbf{A})^{-1}\textbf{u}= s^{-1}\textbf{v},$ iz čega slijedi

$s\textbf{u}=(z-\textbf{A})\textbf{v} =z \textbf{v} - \textbf{Av}.$ Želimo pokazati da je

$z \in \sigma (\textbf{A}+ \textbf{E})$ za neku matricu

$\Vert \textbf{E}\Vert \le \varepsilon$ . Za to je dovoljno pokazati da postoji matrica

$\textbf{E} \in \mathbb{C}^{N \times N}$ takva da vrijedi

$\Vert \textbf{E}\Vert \le s$ i

$\textbf{E}\textbf{v} = s\textbf{u}$ . Naime, ako takva matrica postoji, tada je

$\textbf{v}$ svojstveni vektor matrice

$\textbf{A}+\textbf{E}$ s pripadnom svojstvenom vrijednošću z:

$(\textbf{A}+ \textbf{E}) \textbf{v} = z \textbf{v}, \quad \Vert \textbf{E}\Vert \le \varepsilon.$ Pokazat ćemo da za

$\textbf{E}$ možemo uzeti matricu ranga

$1$ oblika

$\textbf{E}=s\textbf{u}\textbf{w}^{\ast}$ za neki

$\textbf{w}\in\mathbb{C}^{N}$ t.d.

$\textbf{w}^{\ast}\textbf{v}=1$ .

Ako je

$\Vert \cdot\Vert =\Vert \cdot\Vert _{2}$ tvrdnja je očita uzimanjem

$\textbf{w}=\textbf{v}$ .

U slučaju neke druge norme

$\Vert \cdot\Vert$ , možemo se poslužiti korolarom Hahn–Banachova teorema (vidi npr. [5, str. 60.]) koji garantira postojanje linearnog funkcionala

$\textbf{L}$ na

$\mathbb{C}^{N}$ za koji vrijedi

$\Vert \textbf{L}(\textbf{v})\Vert =1$ i

$\Vert \textbf{L}\Vert =1$ . Budući da su svi linearni funkcionali na

$\mathbb{C}^{N}$ oblika

$\textbf{F}(\textbf{x})=\textbf{y}^{\ast}\textbf{x}$ za neki

$\textbf{y}$ , znači da postoji vektor

$\textbf{w}$ takav da vrijedi

$\textbf{L}(\textbf{x})=\textbf{w}^{\ast}\textbf{x}$ . Sada iz

$\Vert \textbf{E}\textbf{x}\Vert =s\Vert \textbf{u}\textbf{w}^{\ast}\textbf{x}\Vert =s\Vert \textbf{u}\Vert |\textbf{L}(\textbf{x})|\le s\Vert \textbf{x}\Vert \text{ za svaki } \textbf{x}$ i

$\textbf{E}\textbf{v} =s \textbf{u}\textbf{w}^{\ast}\textbf{v}=s\textbf{u}\textbf{L}(\textbf{v}) =s \textbf{u}$ slijedi da

$\textbf{w}$ ima tražena svojstva.

$\ \blacksquare$

Prisjetimo se da su singularne vrijednosti matrice

$\textbf{A}$ svojstvene vrijednosti matrice

$\sqrt{\textbf{A}^{\ast}\textbf{A}}$ . Lako se vidi da u slučaju

$2$ –norme vrijedi

(9)

$\Vert (z-\textbf{A})^{-1}\Vert _{2}=[s_{\min}(z-\textbf{A})]^{-1} \quad \text{i} \quad \Vert (z-\textbf{A})\Vert _{2}=[s_{\max}(z-\textbf{A})],$

gdje

$s_{\min}(z-\textbf{A})$ predstavlja najmanju, a

$s_{\max}(z-\textbf{A})$ najveću singularnu vrijednost matrice

$z-\textbf{A}$ . Ovime dolazimo do četvrte i posljednje definicije pseudospektra u ovom radu.

Definicija 5.(4. definicija pseudospektra) Za

$\Vert \cdot\Vert =\Vert \cdot\Vert _{2}$ ,

$\sigma_{\varepsilon}(\textbf{A})$ je skup svih

$z\in\mathbb{C}$ takvih da vrijedi

(10)

$s_{\min}(z-\textbf{A})\lt \varepsilon.$

Iz (9) je očito da je (10) ekvivalentno s (1), a samim time i s ostalim definicijama pseudospektra prema teoremu 4. U dokazu teorema 4 imali smo matricu

$\textbf{E}=s\textbf{u}\textbf{v}^{\ast}$ ranga

$1$ . Sada

$s$ možemo smatrati najmanjom singularnom vrijednošću, a

$\textbf{u}$ i

$\textbf{v}$ pripadnim lijevim, odnosno desnim singularnim vektorom matrice

$z-\textbf{A}$ .

2Pseudospektar normalnih matrica

Za početak primijetimo da ako je

$\textbf{U}$ unitarna matrica (

$\textbf{U}^{\ast}=\textbf{U}^{-1}$ ), tada vrijedi

(11)

$(z-\textbf{UAU}^{\ast})^{-1}=[\textbf{U}(z-\textbf{A})\textbf{U}^{\ast}]^{-1}=\textbf{U}(z-\textbf{A})^{-1}\textbf{U}^{\ast}$

te zbog toga vrijedi i

$\Vert (z-\textbf{UAU}^{\ast})^{-1}\Vert _{2} = \Vert (z-\textbf{A})^{-1}\Vert _{2}, \quad \forall z \in \mathbb{C}.$ To povlači da je norma rezolvente invarijantna na unitarno slične transformacije, te da isto pravilo vrijedi i za pseudospektar:

(12)

$\sigma_{\varepsilon}(\textbf{A})=\sigma_{\varepsilon}(\textbf{UAU}^{\ast}), \quad \forall\varepsilon\geq 0.$

Definicija 6. Matrica

$\textbf{A} \in \mathbb{C}^{N \times N}$ je normalna ako ima potpun skup ortogonalnih svojstvenih vektora tj. ako je unitarno dijagonalizabilna:

(13)

$\textbf{A} = \textbf{U} \Lambda \textbf{U}^{\ast},$

gdje je

$\textbf{U}$ unitarna matrica, a

$\Lambda$ dijagonalna matrica sa svojstvenim vrijednostima na dijagonali.

Napomena 7. Ekvivalentna definicija kaže da je matrica

$\textbf{A} \in \mathbb{C}^{N \times N}$ normalna ako vrijedi

$\textbf{AA}^{\ast}=\textbf{A}^{\ast}\textbf{A}$ .

Dakle, normalna matrica je matrica koja ima posebno svojstvo da postoji unitarna transformacija koja je transformira u dijagonalnu matricu. Za normalnu matricu,

$\varepsilon$ -pseudospektar je zapravo unija otvorenih

$\varepsilon$ -kugli oko točaka spektra matrice (vidi sliku 1). Tada norma rezolvente zadovoljava:

(14)

$\Vert (z-\textbf{A})^{-1}\Vert _{2}=\frac{1}{\text{dist}(z,\sigma(\textbf{A}))},$

gdje

$\text{dist}(z,\sigma(\textbf{A}))$ predstavlja uobičajenu udaljenost točke z od skupa

$\sigma(\textbf{A})$ u kompleksnoj ravnini.

Prije nego što iskažemo idući teorem, objasnit ćemo notaciju kojom ćemo se koristiti. Otvorenu

$\varepsilon$ -kuglu označavat ćemo s

(15)

$\Delta_{\varepsilon}= \lbrace z \in \mathbb{C} : |z|\lt \varepsilon \rbrace .$

Suma dvaju skupova imat će uobičajeno značenje te će vrijediti:

$\sigma(\textbf{A})+\Delta_{\varepsilon} = \lbrace z : z_{1} + z_{2}, z_{1} \in \sigma(\textbf{A}), z_{2} \in \Delta_{\varepsilon} \rbrace = \lbrace z: \text{dist}(z,\sigma(\textbf{A}))\lt \varepsilon \rbrace .$

Teorem 8.(Pseudospektar normalnih matrica) Za bilo koju matricu

$\textbf{A} \in \mathbb{C}^{N \times N}$ vrijedi

(16)

$\sigma_{\varepsilon}(\textbf{A})\supseteq \sigma(\textbf{A})+\Delta_{\varepsilon}, \quad \forall\varepsilon\gt 0,$

a ako je

$\textbf{A}$ normalna i

$\Vert \cdot\Vert =\Vert \cdot\Vert _{2}$ , tada je

(17)

$\sigma_{\varepsilon}(\textbf{A}) = \sigma(\textbf{A})+\Delta_{\varepsilon}, \quad \forall\varepsilon\gt 0.$

Obratno, ako je

$\Vert \cdot\Vert =\Vert \cdot\Vert _{2}$ , tada (17) povlači da je

$\textbf{A}$ normalna matrica.

Dokaz. Ako je z svojstvena vrijednost matrice

$\textbf{A}$ , tada je i

$z+\delta$ svojstvena vrijednost od

$\textbf{A}+\delta\textbf{I}$ za

$\forall\delta\in\mathbb{C}$ . Budući da je

$\Vert \delta\textbf{I}\Vert =|\delta|$ , (16) vrijedi. Za dokazivanje (17) primijetimo da ako je

$\textbf{A}$ normalna, možemo bez smanjenja općenitosti pretpostaviti da je i dijagonalna. Pretpostavka neće imati nikakvog utjecaja na norme ako je

$\Vert \cdot\Vert =\Vert \cdot\Vert _{2}$ . Dijagonalni elementi matrice

$\textbf{A}$ tada su jednaki svojstvenim vrijednostima

$\lambda_{j}$ . Tada je i rezolventa dijagonalna matrica te zbog toga vrijedi (14). Definicija 1 pseudospektra tada povlači (17).

Za dokaz obrata definirajmo najprije skup

$\tau_{\varepsilon} (\textbf{A})= \lbrace z \in \mathbb{C} : \Vert (\textbf{A} - z)^{-1} \Vert _{2} ^{-1} \lt \varepsilon \rbrace$ . Tada znamo da vrijedi

(18)

$\tau_{\varepsilon} (\textbf{A})= \sigma (\textbf{A}) + \Delta_{\varepsilon} = \lbrace z \in \mathbb{C} : \text{dist} (z, \sigma(\textbf{A})) \lt \varepsilon \rbrace , \quad \forall \varepsilon \gt 0.$

Također vrijedi

$\bigcap_{n \in \mathbb{N}} \tau_{\varepsilon + \frac{1}{n}} = \bigcap_{n \in \mathbb{N}} \sigma(\textbf{A})+ \Delta_{\varepsilon + \frac{1}{n}}.$ Lako se vidi da vrijedi

$\bigcap_{n \in \mathbb{N}} \tau_{\varepsilon + \frac{1}{n}} = \lbrace z \in \mathbb{C} : \Vert (\textbf{A}-z)^{-1} \Vert _{2} ^{-1} \leq \varepsilon \rbrace$ te

$\bigcap_{n \in \mathbb{N}} \sigma(\textbf{A})+ \Delta_{\varepsilon + \frac{1}{n}} = \lbrace z \in \mathbb{C} : \text{dist} (z, \sigma(\textbf{A}))\leq \varepsilon \rbrace .$ Stoga vrijedi i

$\tau_{\varepsilon} ^{c} \, \bigcap \, \bigg( \bigcap_{n \in \mathbb{N}} \tau_{\varepsilon + \frac{1}{n}} \bigg) = (\sigma(\textbf{A}) + \Delta_{\varepsilon})^{c} \, \bigcap \, \bigg( \bigcap_{n \in \mathbb{N}} \sigma(\textbf{A}) + \Delta_{\varepsilon + \frac{1}{n}} \bigg),$ što se može zapisati i kao

(19)

$\lbrace z \in \mathbb{C} : \Vert (\textbf{A} - z)^{-1} \Vert _{2} ^{-1} = \varepsilon \rbrace = \lbrace z \in \mathbb{C} : \text{dist} (z, \sigma(\textbf{A})) = \varepsilon \rbrace \quad \forall \varepsilon \gt 0.$

Neka je

$\text{A}=\textbf{ULU}^{\ast}$ Schurova dekompozicija matrice

$\textbf{A}$ , gdje je

$\textbf{L}$ donjetrokutasta matrica ([4]). Tada su dijagonalni elementi matrice

$\textbf{L}$ svojstvene vrijednosti od

$\textbf{A}$ , te vrijedi

$(\textbf{A} - z)^{-1} = (\textbf{ULU}^{\ast} - z)^{-1} = (\textbf{U} (\textbf{L} - z) \textbf{U}^{\ast})^{-1} = \textbf{U} (\textbf{L}-z)^{-1} \textbf{U}^{\ast}$ te stoga vrijedi i

(20)

$\Vert (\textbf{A}-z)^{-1} \Vert _{2} = \Vert (\textbf{L}-z)^{-1} \Vert _{2}.$

Ako pokažemo da je

$\textbf{L} = [ \varphi_{i j } ]$ dijagonalna matrica, onda smo gotovi jer je tada očito

$\textbf{A}$ normalna matrica.

Odaberemo proizvoljan

$i_{0} \in \lbrace 1, \ldots , N \rbrace$ te neke

$z \in \mathbb{C}$ i

$\varepsilon \gt 0$ takve da

$\min_{i} | \varphi_{ii} - z | = | \varphi_{i_{0} i_{0}} - z | = \varepsilon$ . To znači da vrijedi

$\text{dist} (z, \sigma(\textbf{A})) = \varepsilon$ , te stoga po pretpostavci vrijedi

$\Vert (\textbf{A} - z)^{-1} \Vert _{2} ^{-1} = \varepsilon$ , tj.

(21)

$\Vert (\textbf{L} - z)^{-1} \Vert _{2} = \frac{1}{\varepsilon}.$

Izračunajmo sada

$\Vert (\textbf{L}-z)^{-1} \Vert _{2}$ . Znamo da vrijedi

$\Vert (\textbf{L} - z)^{-1} \Vert _{2} = \lambda_{\max} [ (\textbf{L}-z)^{-1} (\textbf{L}-z)^{-\ast} ]$ , a kako je

$\textbf{L}-z = \left[ \begin{array}{cccc} \varphi_{11} - z & 0 & \ldots & 0 \\ \varphi_{12} & \varphi_{22}-z & \ddots & 0 \\ \vdots & \vdots & \ddots & 0\\ \varphi_{1n} & \varphi_{2n} & \cdots & \varphi_{nn}-z \end{array} \right],$ lako je vidjeti da je inverz matrice

$\textbf{L} - z$ ponovno donjetrokutasta matrica oblika

(22)

$(\textbf{L}-z)^{-1} = \left[ \begin{array}{cccc} (\varphi_{11} - z)^{-1} & 0 & \ldots & 0 \\ * & (\varphi_{22}-z)^{-1} & \ddots & 0 \\ \vdots & \vdots & \ddots & 0\\ * & * & \cdots & (\varphi_{nn}-z)^{-1} \end{array} \right].$

Nadalje,

$(\textbf{L}-z)^{-1} (\textbf{L}-z)^{-\ast}$ je hermitska matrica, što povlači

$\sigma(\textbf{A}) \geq \text{diag} ( (\textbf{L}-z)^{-1} (\textbf{L}-z)^{-\ast} )$ ([4]). Stoga

$\begin{align*} \Vert ( \textbf{L}-z)^{-1} \Vert _{2} ^{2} & \geq \max_{i} \bigg( ( \textbf{L}-z)^{-1} (\textbf{L}-z)^{-\ast} \bigg)_{ii} \\ & = \max_{i} \bigg(\sum_{j=1} ^{i-1} \left| \big((\textbf{L}-z)^{-1} \big)_{ij} \right|^{2} + \left| \varphi_{ii}-z \right|^{-2} \bigg) \\ & \geq | \varphi_{i_{0} i_{0}} |^{-2} + \sum_{j=1} ^{i_{0} - 1} \left| \big((\textbf{L}-z)^{-1}\big)_{i_{0} j} \right|^{2} \\ & = \frac{1}{\varepsilon^{2}} +\sum_{j=1} ^{i_{0} -1} \left| \big( (\textbf{L}-z)^{-1}\big)_{i_{0} j} \right|^{2}. \end{align*}$ Budući da je

$\Vert (\textbf{L}-z)^{-1} \Vert _{2} ^{2} = \frac{1}{\varepsilon^{2}}$ , slijedi da je

$((\textbf{L}-z)^{-1})_{i_{0} j}=0$ za

$j=1, \ldots , i_{0}-1$ . Budući da je

$i_{0}$ bio proizvoljno odabran, slijedi da je

$(\textbf{L}-z)^{-1}$ dijagonalna matrica, što povlači da je

$\textbf{L}$ dijagonalna matrica te smo dokazali tvrdnju.

$\ \blacksquare$

3Svojstva pseudospektra

Pretpostavimo da je matrica

$\textbf{A}$ dijagonalizabilna, ali ne nužno i normalna. Neka

$\textbf{V} \in \mathbb{C}^{N \times N}$ predstavlja matricu svojstvenih vrijednosti matrice

$\textbf{A}$ , pri čemu vrijedi:

$\textbf{A}=\textbf{V}\Lambda \textbf{V}^{-1},$ gdje je

$\Lambda$ dijagonalna

$N \times N$ matrica sa svojstvenim vrijednostima

$\lambda_{j}$ na dijagonali. Ako je

$\Vert \cdot \Vert =\Vert \cdot \Vert _{2}$ , onda je kondicijski broj ove baze svojstvenih vektora dan s

(23)

$\kappa (\textbf{V}) \equiv \Vert \textbf{V}\Vert _{2} \Vert \textbf{V}^{-1} \Vert _{2} = \frac{s_{\max}(\textbf{V})}{s_{\min}(\textbf{V})},$

pri čemu su

$s_{\max}(\textbf{V})$ i

$s_{\min}(\textbf{V})$ najveća i najmanja singularna vrijednost matrice

$\textbf{V}$ . Budući da matrica

$\textbf{V}$ nije jedinstvena,

$\kappa (\textbf{V})$ nije jedinstveno definiran za danu matricu

$\textbf{A}$ . No, ako su sve svojstvene vrijednosti matrice

$\textbf{A}$ različite,

$\kappa (\textbf{V})$ postaje jedinstven ako normaliziramo svojstvene vektore (

$\Vert \textbf{v}_{j}\Vert =1$ ).

Općenito, za

$\kappa (\textbf{V})$ vrijedi

$1 \leq \kappa (\textbf{V}) \lt \infty$ , a

$\kappa (\textbf{V})=1$ ako i samo ako je matrica

$\textbf{A}$ normalna. Kondicija matrice

$\textbf{V}$ daje nam gornju granicu za kondicije pojedinačnih svojstvenih vrijednosti matrice

$\textbf{A}$ . Ovime dolazimo do Bauer-Fikeova teorema.

Teorem 9.(Bauer-Fikeov teorem) Neka je

$\textbf{A} \in \mathbb{C}^{N \times N}$ dijagonalizabilna matrica,

$\textbf{A}=\textbf{V}\Lambda \textbf{V}^{-1}$ . Tada, uz

$\Vert \cdot \Vert =\Vert \cdot \Vert _{2},$

$\forall \varepsilon \gt 0$ vrijedi

(24)

$\sigma(\textbf{A}) + \Delta_{\varepsilon} \subseteq \sigma_{\varepsilon} (\textbf{A}) \subseteq \sigma(\textbf{A}) + \Delta_{\varepsilon\kappa(\textbf{V})}.$

Dokaz. Prva inkluzija je dokazana u (16). Za dokazivanje druge inkluzije u tvrdnji teorema računamo:

$(z-\textbf{A})^{-1}= (z- \textbf{V}\Lambda \textbf{V}^{-1})^{-1}=[\textbf{V}(z-\Lambda)\textbf{V}^{-1}]^{-1}= \textbf{V}(z-\Lambda)^{-1}\textbf{V}^{-1},$
što povlači

$\Vert (z-\textbf{A})^{-1}\Vert _{2} \leq \kappa (\textbf{V}) \Vert (z-\Lambda)^{-1}\Vert _{2} = \frac{\kappa(\textbf{V})}{\text{dist}(z,\sigma (\textbf{A}))}.$ Sada dokaz slijedi iz definicije 1.

$\ \blacksquare$

Sljedeći teorem navodi neka od osnovnih svojstava pseudospektra.

Teorem 10. (Svojstva pseudospektra) Neka je

$\textbf{A} \in \mathbb{C}^{N \times N}$ i

$\varepsilon \gt 0$ proizvoljan.

(1)	$\sigma_{\varepsilon}(\textbf{A})$ je neprazan, otvoren i ograničen skup, s najviše N komponenti povezanosti, od kojih svaka komponenta sadržava jednu ili više svojstvenih vrijednosti.
(2)	Ako je $\Vert \cdot \Vert =\Vert \cdot \Vert _{2}$ , tada $\sigma_{\varepsilon}(\textbf{A}^{\ast}) = \overline{\sigma_{\varepsilon}(\textbf{A})}$ .
(3)	Ako je $\Vert \cdot \Vert =\Vert \cdot \Vert _{2}$ , tada $\sigma_{\varepsilon} (\textbf{A}_{1} \oplus \textbf{A}_{2}) = \sigma_{\varepsilon}(\textbf{A}_{1}) \cup \sigma_{\varepsilon}(\textbf{A}_{2})$ .
(4)	Za proizvoljan $c \in \mathbb{C}$ vrijedi $\sigma_{\varepsilon}(\textbf{A}+c)=c+\sigma_{\varepsilon}(\textbf{A})$ .
(5)	Za proizvoljan $c \in \mathbb{C}, c\neq0$ vrijedi $\sigma_{\|c\|\varepsilon}(c\textbf{A})=c\sigma_{\varepsilon} (\textbf{A})$ .

U dijelu

$(iii)$ ,

$\textbf{A}_{1} \oplus \textbf{A}_{2}$ predstavlja direktnu sumu dviju kvadratnih matrica. Pri tome matrice ne moraju biti istih dimenzija, a njihova direktna suma je blok dijagonalna matrica

$\textbf{A}_{1} \oplus \textbf{A}_{2} = \begin{bmatrix} \textbf{A}_{1} & \textbf{0} \\ \textbf{0} & \textbf{A}_{2} \end{bmatrix}.$
Prije nego što započnemo s dokazom teorema, navest ćemo važan rezultat o subharmoničnosti rezolvente kojima ćemo se koristiti u samom dokazu.

Definicija 11.([1)] Neka je

$U$ otvoren podskup od

$\mathbb{C}$ i

$f:U \rightarrow \mathbb{R}$ neprekidna funkcija. Kažemo da je

$f$ subharmonička funkcija na

$U$ ako za svaku zatvorenu kuglu

$\overline{K}(a,r) \subset U$ sa središtem u

$a$ i radijusa

$r$ vrijedi

$f(a) \leq \frac{1}{2 \pi} \int_{0} ^{2 \pi} f(a+re^{i \theta})d\theta.$

Teorem 12.([1], princip maksimuma) Ako je

$S$ ograničen podskup od

$\mathbb{C}$ i

$f : \overline{S} \rightarrow \mathbb{R}$ neprekidna funkcija koja je subharmonička na

$S$ , tada je

(25)

$\sup f(S) = \sup f(\partial S).$

Teorem 13.([3]) Ako je

$f$ holomorfna funkcija na

$S$ , tada je

$\Vert f(\cdot) \Vert$ subharmonička funkcija na

$S$ . Slijedi da

$\Vert f(\cdot) \Vert$ može imati maksimum na skupu

$S$ samo ako je konstantne vrijednosti na cijelom skupu

$S$ .

Korolar 14.([1]) Norma rezolvente

$\Vert (z-\textbf{A})^{-1} \Vert$ je subharmonička funkcija za

$z \not \in \sigma (\textbf{A})$ , što povlači da zadovoljava princip maksimuma. Također vrijedi

(26)

$\Vert (z-\textbf{A})^{-1} \Vert \geq \frac{1}{\text{dist}(z,\sigma(\textbf{A}))}.$

Dokaz teorema 10. Dokazi tvrdnji (ii), (iii) i (iv) su jednostavni pa ih nećemo navoditi.

(i)

Nepraznost, otvorenost i ograničenost skupa

$\sigma_{\varepsilon} (\textbf{A})$ već smo dokazali. Preostaje nam pokazati da se

$\sigma_{\varepsilon} (\textbf{A})$ sastoji od najviše

$N$ komponenti povezanosti, od kojih svaka sadržava jednu ili više svojstvenih vrijednosti. Koristit ćemo se gore navedenim rezultatom.

Pretpostavimo da unutar neke komponente povezanosti nema svojstvenih vrijednosti. Tada je rezolventa holomorfna na tom skupu te je norma rezolvente subharmonička funkcija. Po principu maksimuma, supremum te funkcije dostiže se na rubu te komponente povezanosti. No u našem je slučaju rub podskup skupa

$\lbrace z : \Vert (\textbf{A}-z)^{-1} \Vert = \frac{1}{\varepsilon} \rbrace$ te stoga dolazimo do kontradikcije s činjenicom da je komponenta povezanosti podskup skupa

$\lbrace z : \Vert (\textbf{A}-z)^{-1} \Vert \gt \frac{1}{\varepsilon} \rbrace$ .

Ovime smo tvrdnju dokazali za ograničene komponente povezanosti. Neograničenih komponenti povezanosti uopće ni nema, budući da

$\Vert (\textbf{A}-z)^{-1}\Vert \rightarrow 0$ kad

$|z| \rightarrow \infty$ , te stoga zaključujemo da nema komponenti povezanosti koje ne sadržavaju barem jednu svojstvenu vrijednost matrice

$\textbf{A}$ . Budući da

$\textbf{A}$ ima najviše

$N$ različitih svojstvenih vrijednosti, komponenti povezanosti također može biti najviše

$N$ .

(v)

Pretpostavimo da je

$z \in \sigma_{|c|\varepsilon}(c\textbf{A})$ . Tvrdnja je očigledna ako je

$c=0$ ili

$\varepsilon = 0$ . Stoga, uz

$c \neq 0$ i

$\varepsilon \neq 0$ , definicija 1 pseudospektra povlači da je

$(| c | \varepsilon)^{-1}\lt \Vert (z - c\textbf{A})^{-1} \Vert = | c |^{-1} \Vert (\frac{z}{c} - \textbf{A})^{-1} \Vert .$ Sada je jasno da je

$\frac{z}{c} \in \sigma_{\varepsilon} (\textbf{A})$ , odnosno

$z \in c \sigma_{\varepsilon} (\textbf{A})$ , što je i trebalo pokazati.

$\ \blacksquare$

4Primjeri

Promatrat ćemo tridijagonalnu Toeplitzovu matricu

(27)

$\textbf{A} = \begin{bmatrix} 0 & 1 && \\ \frac{1}{4} & 0 & 1 && \\ & \ddots & \ddots & \ddots & \\ && \frac{1}{4} & 0 & 1\\ &&& \frac{1}{4} & 0\end{bmatrix} \in \mathbb{C}^{N \times N}.$

Iako je ova matrica nesimetrična, možemo je svesti na simetričan oblik sljedećom transformacijom

(28)

$\textbf{DAD}^{-1}=\textbf{S},$

gdje je

$\textbf{D}= \text{diag}(2,4,...,2^{N})$ i

(29)

$\textbf{S} = \begin{bmatrix} 0 & \frac{1}{2} && \\ \frac{1}{2} & 0 & \frac{1}{2} && \\ & \ddots & \ddots & \ddots & \\ && \frac{1}{2} & 0 & \frac{1}{2}\\ &&& \frac{1}{2} & 0 \end{bmatrix} \in \mathbb{C}^{N \times N}.$

Matrice

$\textbf{A}$ i

$\textbf{S}$ imaju iste svojstvene vrijednosti te se može izračunati da se spektar matrice

$\textbf{A}$ sastoji od

$N$ različitih svojstvenih vrijednosti iz intervala

$\langle -1,1\rangle$

(30)

$\lambda_{k} ( \textbf{A} )= \lambda_{k} ( \textbf{S} ) = \cos \frac{k \pi}{N+1}, \quad 1\leq k \leq N.$

S druge strane, pseudospektar matrice

$\textbf{A}$ znatno odudara od realne osi za različite vrijednosti

$\varepsilon$ . Slika 4 prikazuje granice

$\sigma_{\varepsilon}(\textbf{A})$ za

$\varepsilon=10^{-2},10^{-3},...,10^{-8}$ uz

$\Vert \cdot \Vert = \Vert \cdot \Vert _{2}$ i otkriva široka ovalna područja pseudospektra u kompleksnoj ravnini.

$\varepsilon$ -pseudospektar zapravo je približno jednak području koje omeđuje elipsa koja je slika kružnice

$|z|=\varepsilon^{1/N}$ pri preslikavanju

(31)

$f(z)=z^{-1}+\frac{1}{4}z.$

Slika 5 prikazuje svojstvene vrijednosti

$100$ slučajno perturbiranih matrica

$\textbf{A+E}$ , pri čemu vrijedi

$\Vert \textbf{E} \Vert =10^{-3}$ uz

$\Vert \cdot \Vert = \Vert \cdot \Vert _{2}$ . Veza s elipsama ponovno je jasno vidljiva.

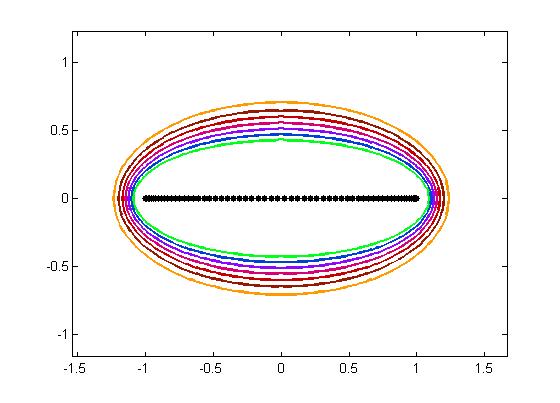
Slika 4: Granice

$\varepsilon$ -pseudospektra

$\sigma_{\varepsilon} (\textbf{A})$ u

$2$ -normi za

$\varepsilon=10^{-2},10^{-3},...,10^{-8}$ matrice (27) dimenzije

$N=64$ . Svojstvene vrijednosti matrice prikazane su crnim točkama.

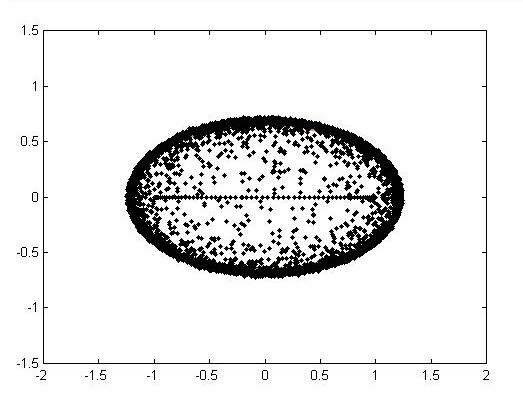
Slika 5: Pozicije svojstvenih vrijednosti 100 matrica

$\textbf{A+E}$ , gdje je

$\textbf{A}$ tridijagonalna Toeplitzova matrica (27) dimenzije

$N=64$ , a svaka

$\textbf{E}$ je slučajna matrica uz

$\Vert \textbf{E} \Vert = 10^{-3}$ . Svojstvene vrijednosti matrice

$\textbf{A}$ su realne, ali perturbacije inducirane matricom

$\textbf{E}$ ih pomiču u kompleksnu ravninu, blizu elipse definirane s (31) uz

$|z|=0.001^{1/64}$ . Ponovno je

$\Vert \cdot \Vert = \Vert \cdot \Vert _{2}$ .

5Povijesni pregled i literatura

Slučajevi u kojima svojstvene vrijednosti i spektar matrice ne daju zadovoljavajuće odgovore na postavljena pitanja usko su vezani uz matrice koje nemaju svojstvo normalnosti. Potrebu za istraživanjem pseudospektra prepoznao je von Neumann još u 1930–ima, no zbog teškoća s velikim brojem složenih računskih operacija i nedovoljnog stupnja razvijenosti računala koja bi ih mogla izvesti, pojam pseudospektra nije zaživio sve do druge polovine 20. stoljeća. Tako na potrebu za istraživanjem pseudospektra ponovno upućuju Varah 1967. i 1979. ([12] i [11]), Landau 1975. ([6]) i Godunov 1982. ([2]). Prvi rad potpuno posvećen pseudospektru pod nazivom „Pseudospectra of matrices” napisao je Trefethen 1992. godine ([9]). U tom je radu iznio osnovnu teoriju pseudospektra popraćenu s 13 primjera. Trefethen nastavlja istraživanje pseudospektra te nekoliko godina poslije izdaje i rad „Pseudospectra of Linear Operators” ([8]) kojim produbljuje teoriju iza ideje pseudospektra i proširuje područje njegove primjene. Tim radovima pseudospektar postaje poznat široj javnosti te se javlja znatno veći interes među znanstvenicima za razradom ovog relativno novog pojma u matematici.

Ovaj članak temelji se na diplomskom radu drugog autora, napisanom pod vodstvom prvog autora [7], koji se pak temelji na knjizi [10].

Bibliografija

[1]	Burkcel, R. B.: An introduction to classical complex analysis, Academic Press, New York, 1979
[2]	Godunov, S. K.: Guaranteed accuracy in numerical linear algebra, Kluwer Academic Publishers, 1993
[3]	Hille, E, i Phillips, R. S.: Functional analysis and semi-groups, AMS, Providence, 1957
[4]	Horn, R. A. i Johnson C. R.: Matrix analysis, Cambridge University Press, 1985
[5]	Kurepa, S.: Funkcionalna analiza, Školska knjiga, Zagreb, 1990.
[6]	Landau, H. J.: On Szegõ's eigenvalue distribution theorem and non-Hermitian kernels, J. d'Analyse Math., no. 28, str. 335.–357., 1975
[7]	Petrić, M.: Pseudospektar, Diplmoski rad, PMF–MO, Sveučilište u Zagrebu, 2010.
[8]	Trefethen, L. N.: Pseudospectra of Linear Operators, SIAM review, vol. 39, no. 3, str. 383.–406., 1997
[9]	Trefethen, L. N.: Pseudospectra of matrices, u Griffiths, D. F. i Watson, G. A. (ur.):Numerical Analysis 1991, str. 234.–266., 1992
[10]	Trefethen, L. N. i Embree, M.: Spectra and pseudospectra: the behavior of nonnormal matrices and operators, Princeton University Press, Princeton, 2005
[11]	Varah, J. M.: On the Separation of Two Matrices, SIAM Journal on Numerical Analysis, vol. 16, no. 2, str. 216.–222., 1979
[12]	Varah, J. M.: The computation of bounds for the invariant subspaces of a general matrix operator, Technical report CS 66, Computer Science Department, Stanford University, 1967

math.e

Secondary links

Novi brojevi časopisa math.e

Kalendar

Rujan

Matematički blogovi

Sponzori

Pseudospektar matrica