|
Zlatko Erjavec, Drago Kovačec |
zlatko.erjavec@foi.hr, drago.kovacec@foi.hr
Sažetak
U članku se pojašnjavaju osnovni pojmovi tropske geometrije te njena primjena u rješavanju problema određivanja najkraćeg puta u težinskom grafu Floyd-Warshallovim algoritmom.
1Uvod
Tropska geometrija je relativno novo područje u matematici, a naziv "tropska geometrija" osmislili su francuski matematičari u čast brazilskom matematičaru Imre Simonu, pioniru u tom području. Stoga pridjev "tropska" nema neko posebno značenje osim asocijacije na Brazil kao tropsko područje.
Jednostavnost aritmetike tropske geometrije omogućila joj je brojne primjene od ekonomije preko biologije do računarstva. Više o primjenama može se naći u [2].
U ovom članku pokazat ćemo na koji se način aritmetika tropske geometrije može primijeniti u rješavanju problema pronalaska najkraćeg puta. Bilo da govorimo o putu kamiona od skladišta do odredišta ili o najkraćem putu među serverima u računalnoj mreži, problem se svodi na nalaženje najkraćeg puta u težinskom grafu. Navedeni problem rješava Floyd-Warshallov algoritam.
2Tropska geometrija
Osnovna struktura tropske geometrije je tropski poluprsten, uređena trojka \left(\mathbb{R }\cup \, \lbrace \infty \rbrace , \ \oplus ,\ \odot \right) sastavljena od skupa realnih brojeva proširenog beskonačnošću te dvije međusobno usklađene operacije, tropskog zbrajanja i tropskog množenja (vidi [3]).
2.1Tropsko zbrajanje
Suma dvaju brojeva u tropskoj aritmetici definira se kao minimum tih dvaju brojeva
(1)
x \oplus y := \min (x, y).
Primjer 1. Tropsko zbrajanje
3 \oplus 5= 3 \qquad \text{i} \qquad 7 \oplus 2 = 2.
2.2Tropsko množenje
Produkt dvaju brojeva u tropskoj aritmetici definira se kao uobičajen zbroj tih dvaju brojeva
Primjer 2. Tropsko množenje
3 \odot 5 = 8 \qquad \text{ i} \qquad 7 \odot 2 = 9.
Obje definirane računske operacije imaju neutralne elemente. Za tropsko zbrajanje neutralni element je beskonačno, dok je za tropsko množenje neutralni element nula
a \oplus \infty = a\qquad \text{ i} \qquad a \odot 0 = a.
Također vrijedi,
a \oplus 0 = \begin{cases} 0 ,& \text{za}\ a\geq 0\\ a ,& \text{za}\ a\lt 0 \\ \end{cases} \qquad \text{ i} \qquad a \odot \infty = \infty.
Nadalje, obje operacije su komutativne i asocijativne te vrijedi distributivnost množenja u odnosu na zbrajanje.
|
\bullet |
Komutativnost
a \oplus b = b \oplus a \qquad \text{ i} \qquad a \odot b = b \odot a.
|
|
\bullet |
Asocijativnost
(a \oplus b) \oplus c = a \oplus (b \oplus c) \quad \text{ i} \quad (a \odot b) \odot c = a \odot (b \odot c).
|
|
\bullet |
Distributivnost
a \odot (b \oplus c) = a \odot b \oplus a \odot c.
|
Primjer 3. Distributivnost tropskog množenja prema zbrajanju
\begin{eqnarray*} 4 \odot (2 \oplus 3) &=& 4 \odot 2 \oplus 4 \odot 3\\ 4 \odot 2 &=& 6 \oplus 7 \\ 6 &=& 6. \end{eqnarray*}
2.3Tropski polinom
Neka su x_{1}, x_{2}, \ldots x_{n} varijable koje predstavljaju elemente tropskog poluprstena. Monom se definira kao bilo koji produkt tih varijabli, pri čemu je mogućnost njihova ponavljanja dozvoljena.
Koristeći komutativnost i asocijativnost, možemo presložiti produkt i zapisati ga u uobičajenom obliku koristeći potencije, imajući na umu da x^{2} znači x \odot x, a ne x \cdot x. Npr.
x_{2} \odot x_{1} \odot x_{3} \odot x_{1} \odot x_{2} \odot x_{2} = x_{1}^{2}\,x_{2}^{3}\,x_{3}.
Svakom monomu možemo pridružiti funkciju sa \mathbb{R}^{n} u \mathbb{R}. Kada bismo takvu funkciju evaluirali u klasičnoj aritmetici, dobili bismo linearnu funkciju:
\begin{eqnarray*} f(x_{1}, x_{2}, x_{3})&=& x_{2} \odot x_{1} \odot x_{3} \odot x_{1} \odot x_{2} \odot x_{2} \\ &=& x_{2} + x_{1} + x_{3} + x_{1} + x_{2} +x_{2} \\ &=& 2 x_{1}+ 3x_{2} +x_{3}. \end{eqnarray*}
Iako smo u primjeru koristili pozitivne eksponente, monomi su definirani i za cjelobrojne eksponente. Stoga, možemo zaključiti da su tropski monomi linearne funkcije s cjelobrojnim koeficijentima.
Tropski polinom je konačna linearna kombinacija tropskih monoma: p(x_{1}, x_{2}, \ldots x_{n})=a \odot x_{1}^{i_{1}} x_{2}^{i_{2}} \cdots x_{n}^{i_{n}} \oplus b \odot x_{1}^{j_{1}} x_{2}^{j_{2}} \cdots x_{n}^{j_{n}} \oplus \cdots
Primjer 4. Tropski polinom u jednoj varijabli
p(x)=(2 \odot x^{3} ) \oplus (1\odot x^{2} ) \oplus (3 \odot x) \oplus 2= \min \lbrace 2+3x, 1+2x, 3+x, 2\rbrace.
Primijetite da u tropskoj geometriji polinomi
\begin{eqnarray*} p_{1}(x)&=&x^{2} \oplus (1 \odot x) \oplus 2= \min \lbrace 2x, 1+x, 2\rbrace = \min \lbrace 2x, 2\rbrace \quad \text{i} \\ p_{2}(x)&=&x^{2} \oplus (17 \odot x) \oplus 2= \min \lbrace 2x, 17+x, 2\rbrace = \min \lbrace 2x, 2\rbrace \end{eqnarray*}
imaju istu vrijednost. Dakle, prikaz neke funkcije u obliku tropskog polinoma nije jednoznačan.
Uslijed specifičnosti definicije množenja i nule kao neutralnog elementa, svi binomni koeficijenti tropskog polinoma jednaki su nuli (u Pascalovom trokutu su samo nule!). Posljedica navedenog je činjenica da u tropskoj geometriji za sve potencije binoma vrijedi tzv. "brucoški san".
Primjer 5. "Brucoški san" za kvadrat binoma
\begin{eqnarray*}(x \oplus y)^{2} &=& (x \oplus y) \odot (x \oplus y)\\ &=& 0 \odot x^{2} \oplus 0 \odot xy \oplus 0 \odot y^{2} \\ &=& (0 + x^{2}) \oplus (0 + xy) \oplus (0 + y^{2}) \\ &=& x^{2} \oplus xy \oplus y^{2} \\ &=& \min \lbrace x^{^{2}}, xy, y^{2} \rbrace \\ &=& \min \lbrace x^{^{2}}, y^{2} \rbrace \\ &=& x^{2} \oplus y^{2}. \end{eqnarray*}
2.4Tropski skalarni produkt
Tropski skalarni produkt definira se analogno klasičnom matričnom produktu jednoretčane i jednostupčane matrice
\begin{eqnarray*} (u_{1}, u_{2}, u_{3}) \odot (v_{1}, v_{2}, v_{3})^{T} &=& u_{1} \odot v_{1} \oplus u_{2} \odot v_{2} \oplus u_{3} \odot v_{3} \\ &=& \min \left\lbrace u_{1} + v_{1}, u_{2} + v_{2}, u_{3} + v_{3} \right\rbrace. \end{eqnarray*}
Primjer 6. Tropski skalarni produkt
\begin{eqnarray*}(2, 4, -3) \odot (3, 5, -5) &=& (2 \odot 3) \oplus (4 \odot 5) \oplus ((-3) \odot (-5))\\ & =& \min \lbrace 5, 9, -8\rbrace =-8.\end{eqnarray*}
2.5Tropsko zbrajanje matrica
Tropsko zbrajanje matrica definira se analogno klasičnom zbrajanju matrica, po elementima, korištenjem tropskog zbrajanja.
Primjer 7. Tropsko zbrajanje matrica
\begin{pmatrix} 0 & 2 \\ 3 & 1 \end{pmatrix} \oplus \begin{pmatrix} 3 & 1 \\ 1 & 1 \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ 1 & 1 \end{pmatrix}.
2.6Tropsko množenje matrica
Tropsko množenje matrica definira se analogno klasičnom množenju matrica. Element produkta dviju matrica dobije se kao tropski skalarni produkt odgovarajućeg retka prve i odgovarajućeg stupca druge matrice.
Primjer 8. Tropsko množenje matrica
\begin{pmatrix} 0 & 2 \\ 3 & 1 \end{pmatrix} \odot \begin{pmatrix} 3 & 1 \\ 1 & 1 \end{pmatrix} = \begin{pmatrix} 3 & 1 \\ 2 & 2 \end{pmatrix}.
3Grafovi i problem najkraćeg puta
Graf G se definira kao uređen par skupova G=(V, E) pri čemu je skup V skup vrhova, a skup E je skup bridova. Skupovi V i E su disjunktni, a svaki brid e \in E spaja dva vrha u, v \in V. Vrhovi u, v grafa G se još nazivaju krajevima brida e (vidi [1]).
Šetnja u grafu G je konačan niz incidentnih vrhova i bridova. Vrhovi i bridovi u šetnji ne moraju nužno biti i različiti.
Šetnja u kojoj su svi vrhovi i bridovi različiti zove se put. Primjer jednog puta u grafu sa Slike 1 je P = v_{1}\, e_{1}\, v_{2}\, e_{3}\, v_{4}\, e_{6}\, v_{5}\, e_{7}\, v_{6}.
Graf prikazan na Slici 1 nazivamo i neusmjerenim grafom zato što je bridovima grafa moguće prolaziti u oba smjera.
Usmjereni brid zovemo lukom, a ukoliko se svi bridovi grafa orijentiraju (usmjere), tada graf zovemo usmjerenim grafom. Lukovima usmjerenog grafa moguće je prolaziti samo u smjeru orijentacije.
Pridružimo li svakom bridu nenegativan realan broj w(e), dobiveni graf naziva se težinski graf, a broj pridružen bridu e težina brida w(e).
Težinski graf kojem su svi bridovi usmjereni zovemo težinski usmjerenim grafom.
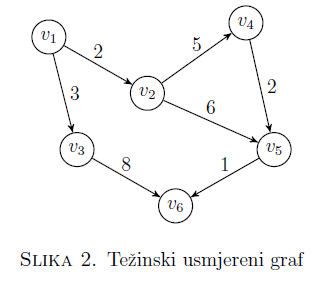
Težinu puta P u grafu G možemo definirati formulom
w(P)= \sum_{e \in {E} (P)} w(e).
Drugim riječima, težina puta P u grafu G je zbroj težina svih bridova kojima se prolazi od početnog do završnog vrha puta P. Tako bi težina puta P = v_{1} \, e_{1}\, v_{2}\, e_{3} \, v_{4}\, e_{6}\, v_{5}\, e_{7}\, v_{6} u grafu sa Slike 1 (uzimajući u obzir težine dane na Slici 2) iznosila 10, dok je istovremeno težina puta Q=v_{1}\, e_{1}\, v_{2}\, e_{4}\, v_{5}\, e_{7}\, v_{6} u grafu sa iste slike 9.
Ukoliko nam je cilj što razumnije koristiti resurse, bilo da se radi o udaljenosti koju trebaju proći automobilom ili vremenu potrebnom za prijenos informacija, htjeli bismo da težina puta između dva vrha bude najmanja moguća. Problem pronalaska takvog puta zovemo problemom najkraćeg puta, a rješenje problema dano je algoritmom koji nazivamo Floyd-Warshallov algoritam.
4Floyd-Warshallov algoritam u tropskoj geometriji
Floyd-Warshallov algoritam je algoritam za pronalaženje najkraćeg puta između bilo koja dva povezana vrha u težinskom grafu.
Obzirom da se računanje svodi na uzastopne transformacije matrica, prednost ovog algoritma je što kod izvršavanja na računalu ne troši velike memorijske resurse.
U nastavku ćemo pojasniti korake algoritma. Odabere se prvi vrh te se redom izračunavaju udaljenosti od tog vrha do svih preostalih vrhova s kojima je on povezan. Ukoliko je promatrani vrh s nekim drugim vrhom povezan s više puteva, tada se za udaljenost između ta dva vrha uzima najmanja udaljenost između ta dva vrha. Ponavljanjem istog postupka za svaki od preostalih vrhova dobiju se najkraće udaljenosti između vrhova u grafu.
Pseudokod Floyd-Warshallovog algoritma
ulaz: Težinski graf G = (V, E), V = v_{1}, v_{2},\ldots, v_{n}
izlaz: Najkraće udaljenosti između svaka dva vrha u grafu G
|
(1) |
Za i = 1, \ldots, n stavi d(i, i) = 0. Za i \ne j, ako je v_{i}v_{j} brid, stavi d(i, j) =w(v_{i}v_{j}), inače stavi d(i, j) = \infty. |
|
(2) |
Za k = 1, \ldots, n
|
\bullet |
za i, j = 1, \ldots, n |
|
\bullet |
d(i, j) := d(i, j) \oplus \left( d(i, k) \odot d(k, j) \right) |
|
Kada bismo usporedili prikazani pseudokod s klasičnim, zaključili bismo da su samo uobičajene operacije minimuma i zbrajanja zamijenjene tropskim zbrajanjem i množenjem.
No snaga primjene tropske geometrije u ovom slučaju je puno veća. U nastavku ćemo pokazati da se traženje najkraćeg puta u težinskom grafu uz pomoć tropske geometrije svodi na tropsko množenje matrica.
Svakom težinskom grafu možemo pridružiti matricu susjedstva na sljedeći način
D_{(i,j)} =\begin{cases} w(v_{i},v_{j}), & \text{ako su} v_{i} \text{ i } v_{j} \text{ susjedni}\\ 0 ,& \text{ako je}\, i=j \\ \infty, & \text{ako } v_{i} \text{ i } v_{j} \text{ nisu susjedni.} \end{cases}
Primjer 9. Matrica susjedstva grafa sa Slike
2
D=\begin{pmatrix} 0 & 2 & 3 & \infty & \infty & \infty \\ \infty & 0 & \infty & 5 & 6 & \infty \\ \infty & \infty & 0 & \infty & \infty & 8 \\ \infty & \infty & \infty & 0 & 2 & \infty \\ \infty & \infty & \infty & \infty & 0 & 1 \\ \infty & \infty & \infty & \infty & \infty & 0 \end{pmatrix}.
Također, za proizvoljnu kvadratnu matricu, u tropskoj se geometriji definira k-ta tropska potencija matrice kao tropski umnožak k matrica
D^{\odot k}:=\underbrace{D \odot D \odot \cdots \odot D}_{k \ \text{puta}}.
Teorem 1. Neka je G težinski usmjeren graf s n vrhova i n \times n matricom susjedstva D. Tada je element matrice D^{\odot n-1} na poziciji (i,j) jednak duljini najkraćeg puta od vrha v_{i} do vrha v_{j}.
Dokaz. Neka je s
d_{ij}^{(r)} označena minimalna duljina bilo kojeg puta od vrha
v_{i} do vrha
v_{j} koji prolazi kroz najviše
r bridova u grafu
G.
Neka je
d_{ij}^{(1)} = d_{ij} za bilo koja dva vrha
v_{i} i
v_{j}. Pretpostavivši da su težine bridova nenegativne vrijednosti, najkraći put od
v_{i} do
v_{j} prolazi najviše jednom kroz svaki vrh u grafu
G. Općenito, bilo koji najkraći put u težinski usmjerenom grafu
G prelazi kroz najviše
n-1 usmjerenih bridova. Otuda slijedi da je duljina najkraćeg puta od vrha
v_{i} do vrha
v_{j} jednaka
d_{ij}^{(n-1)}.
Za
r\geq 2 imamo sljedeću rekurzivnu formulu za duljinu najkraćeg puta
(3)
d_{ij}^{(r)} = \min \left\lbrace d_{ik}^{(r-1)} + d_{kj} \ : k = 1, 2,\ldots, n \right\rbrace .
Korištenjem tropske aritmetike prethodna formula može se zapisati na sljedeći način
\begin{eqnarray*} d_{ij}^{(r)}&=& d_{i1}^{(r-1)} \odot d_{1j} \oplus d_{i2}^{(r-1)} \odot d_{2j} \oplus ... \oplus d_{in}^{(r-1)} \odot d_{nj} \\ &=& (d_{i1}^{(r-1)}, d_{i2}^{(r-1)}, \ldots, d_{in}^{(r-1)}) \odot (d_{1j}, d_{2j}, \ldots, d_{nj})^{T}. \end{eqnarray*}
Iz navedenog proizlazi da se
d_{ij}^{(r)} podudara sa elementom u
i-tom retku i
j-tom stupcu matrice
D^{\odot r}. Očito je desna strana rekurzivne formula tropski produkt
i-tog retka matrice
D^{\odot r-1} i
j-tog stupca matrice
D. Indukcijom po
r zaključujemo da se
d_{ij}^{(n-1)} podudara s elementom u
i-tom retku i
j-tom stupcu matrice
D^{\odot n-1}
\ \blacksquare
Primjer 10. Računanje elementa matrice
D na poziciji
(1,4)
\begin{eqnarray*} d^{(1)}_{1,4} &=& ( 0 \odot \infty ) \oplus (2 \odot 5) \oplus (3 \odot \infty) \oplus (\infty \odot 0) \oplus (\infty \odot \infty) \oplus (\infty \odot \infty) \\ &=& \infty \ \oplus \ 7 \oplus \ \infty \ \oplus \ \infty \ \oplus \ \infty \ \oplus \ \infty \\ &=& \min \left\lbrace { \infty, 7, \infty, \infty, \infty, \infty} \right\rbrace \\ &=& 7. \end{eqnarray*}
Primjer 11. Matrica najkraćih puteva grafa sa Slike
2
D^{\odot 5}=\begin{pmatrix} 0 & 2 & 3 & 7 & 8 & 9 \\ \infty & 0 & \infty & 5 & 6 & 7\\ \infty & \infty & 0 & \infty & \infty & 8 \\ \infty & \infty & \infty & 0 & 2 & 3 \\ \infty & \infty & \infty & \infty & 0 & 1 \\ \infty & \infty & \infty & \infty & \infty & 0 \end{pmatrix}.
Navedena matrica predstavlja rješenje problema i iz nje se mogu iščitati najkraće udaljenosti između bilo koja dva povezan vrha.
Slijedi da je
d(v_{1},v_{2})=2,
d(v_{1},v_{3})=3,
d(v_{1},v_{4})=7,
d(v_{1},v_{5})=8,
d(v_{1},v_{6})=9,
d(v_{2},v_{4})=5,
d(v_{2},v_{5})=6,
d(v_{2},v_{6})=7,
d(v_{3},v_{6})=8,
d(v_{4},v_{5})=2,
d(v_{4},v_{6})=3 i
d(v_{5},v_{6})=1.
Napomena 12. Primijetite da iako smo pomoću Floyd-Warshallovog algoritma odredili najkraće udaljenosti između vrhova, algoritam ne otkriva putove kojima su najmanje udaljenosti ostvarene.
Primjer 13. Matrica susjedstva težinski neusmjerenog grafa
Zamislimo li da je graf sa Slike
2 težinski neusmjereni graf, tada bi njegova matrica susjedstva bila sljedeća simetrična matrica
\bar{D}=\begin{pmatrix} 0 & 2 & 3 & \infty & \infty & \infty \\ 2 & 0 & \infty & 5 & 6 & \infty \\ 3 & \infty & 0 & \infty & \infty & 8 \\ \infty & 5 & \infty & 0 & 2 & \infty \\ \infty & 6 & \infty & 2 & 0 & 1 \\ \infty & \infty & 8 & \infty & 1 & 0 \end{pmatrix}.
Izračunavanjem pete potencije matrice susjedstva
\bar{D} možemo odrediti simetričnu matricu najkraćih putova težinski neusmjerenog analogona grafa sa Slike
2.
\bar{D}^{\odot 5}=\begin{pmatrix} 0 & 2 & 3 & 7 & 8 & 9 \\ 2 & 0 & 5 & 5 & 6 & 7\\ 3 & 5 & 0 & 10 & 9 & 8 \\ 7 & 5 & 10 & 0 & 2 & 3 \\ 8 & 6 & 9 & 2 & 0 & 1 \\ 9 & 7 & 8 & 3 & 1 & 0 \end{pmatrix}
Bibliografija
|
[1] |
Divjak B., Lovrenčić A. Diskretna matematika s teorijom grafova, FOI-TIVA, Varaždin, 2005. |
|
[2] |
Maclagan D., Sturmfels B., Introduction to Tropical Geometry, AMS Grad Stud in Math Vol 161, 2015. |
|
[3] |
Speyer D., Sturmfels B., Tropical mathematics, Math Magazine 82 (3), 2009, 163–173. |