Matrice s Fibonaccijevim brojevima
U prostranstvu cjelobrojnih nizova Fibonaccijev niz ne gubi svoj sjaj već više od osam stoljeća, točnije od kad se pojavio u knjizi Liber Abaci talijanskog matematičara Leonarda Bonaccija1 poznatog i kao Leonardo Pisano, a najpoznatijeg kao Fibonacci. Bez pretjerivanja, riječ je o jednom od najpoznatijih nizova koji privlači i fascinira kako profesionalce tako i potpune amatere. Nadalje, neprestano iznenađuje sa svojom prisutnošću u očekivanim, ali i potpuno neočekivanim situacijama. O Fibonaccijevim brojevima postoji vrlo velika količina informacija, mnoštvo publikacija, knjiga, te internetskih sadržaja. U ovom radu pokazat ćemo i dokazati neke zanimljive identitete vezane uz Fibonaccijeve brojeve koristeći jednostavnu algebru matrica i determinanti. Između ostalog, pokazujemo i poznati Cassinijev2 identitet koji se se može povezati s problemom popločavanja. Zbog mlađeg čitateljstva navest ćemo osnovna svojstva Fibonaccijevog niza, te osnovne pojmove iz linearne algebre.
Fibonaccijev niz je niz brojeva
1,1,2,3,5,8,13,21,34,55,….Niz bi s lakoćom nastavili članom 89 koji je zbroj prethodna dva. Iskažimo njegovu matematičku definiciju.
Napomenimo da se ponekad za početne vrijednosti niza uzimaju vrijednosti F0=0 i F1=1.
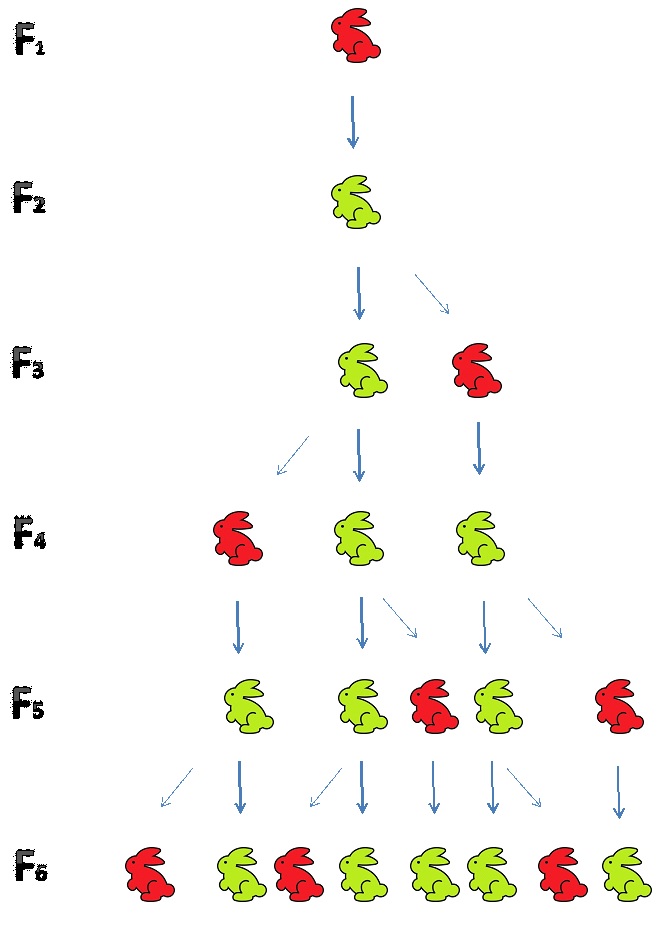
U već spomenutoj knjizi Liber Abaci taj niz predstavlja rješenje problema o razmnožavanju zečeva. Pretpostavimo da 1. siječnja raspolažemo s jednim parom zečeva. Taj par dobiva po jedan par mladih zečeva svakog prvog dana u mjesecu, počevši od 1. ožujka. Svaki novi par dobiva po jedan par zečeva svakog prvog dana u mjesecu, ali tek nakon navršena dva mjeseca života. Problem je koliko će parova zečeva biti nakon n mjeseci. Odgovor je upravo n-ti Fibonaccijev broj Fn.
Eksplicitno, Fibonaccijeve brojeve možemo izračunati pomoću formule
Fn=1√5(αn−βn),pri čemu su α i β korijeni takozvane zlatne jednadžbe
x2−x−1=0,to jest
α=1+√52, β=1−√52.Konstanta α poznatija je pod nazivom zlatni rez.
Uz Fibonaccijev niz često se veže i Lucasov3 niz (Ln) koji je definiran istom rekurzijom
Predodžbe radi, prvih nekoliko članova Lucasova niza su
2,1,3,4,7,11,18,….Eksplicitno ih računamo pomoću formule
Ln=αn+βn.Fibonaccijevi i Lucasovi brojevi zadovoljavaju različite algebarske identitete. Budući da su generirani rekurzivnim relacijama (
Kao primjer navodimo osnovnu relaciju koja povezuje Fibonaccijeve i Lucasove brojevi, to jest
za n≥1. Jednakost pokazujemo pomoću principa matematičke indukcije. Za n=1 jednakost vrijedi jer je
F0+F2=1=L1.Pretpostavimo sada da jednakost vrijedi za n=k, odnosno Lk=Fk−1+Fk+1. Za n=k+1 imamo
Fk+Fk+2=Fk−1+Fk−2+Fk+1+Fk=(Fk−1+Fk+1+(Fk−2+Fk)=Lk+Lk−1=Lk+1,što je i trebalo pokazati.
U onom što slijedi pokazat ćemo kako možemo dokazati i izvesti još identiteta s Fibonaccijevim i Lucasovim brojevima koristeći elementarna svojstva matrica.
Matrica reda 2 je kvadratna shema koja se sastoji od 4 elementa posložena u 2 retka i 2 stupca. Simbolički ju zapisujemo kao
A=(a11a12 a21a22).Elementi matrice a11, a12, a21, a22 su najčešće realni brojevi, pa takvu matricu nazivamo realnom. Elementi matrice su indeksirani tako da nas upućuju na kojoj se poziciji u matrici nalaze. Tako se element a21 nalazi na presjeku drugog retka i prvog stupce. Na skupu svih matrica reda 2 jednostavno uvodimo dvije operacije, zbrajanje matrica i množenje matrica skalarom (realnim brojem). Te se operacije izvršavaju prirodno, 'po elementima'. Dakle,
A+B=(a11a12 a21a22)+(b11b12 b21b22)=(a11+b11a12+b12 a21+b21a22+b22), α⋅A=α(a11a12 a21a22)=(αa11αa12 αa21αa22).Na primjer,
(12 34)+(−4−3 −2−1)=(−3−1 13), 3(12 −10)=(36 −30).Množenje matrica ne ćemo definirati po analogiji i to je prilično neočekivano. Umnožak ili produkt dviju matrica definiramo na sljedeći način
A⋅B=(a11a12 a21a22)⋅(b11b12 b21b22)=(a11b11+a12b21a11b12+a12b22 a21b11+a22b21a21b12+a22b22).Na primjer,
(12 34)⋅(−4−3 −2−1)=(−8−5 −20−13).Zbog ovakve 'neobične' definicije i množenje matrica imat će neka 'neobična' svojstva. Na primjer, općenito ne će vrijediti svojstvo komutativnosti.
Uz matricu reda 2 često vežemo i pojam determinante. To je broj koji pridružujemo matrici, a definiramo ga kao
Zahvaljući 'neobično' definiranom množenju matrica vrijedit će sljedeće važno svojstvo, u matematici poznatije kao Binet-Cauchyjev teorem,
|A\cdot B|=|A|\cdot|B|.Provjerimo to na gornjem primjeru,
\left|\begin{array}{rr} 1 &2 \\\ 3 &4 \end{array} \right|=-2,\ \left| \begin{array}{rr} -4 &-3 \\\ -2 &-1 \end{array} \right|= -2,\left| \begin{array}{rr} -8 &-5 \\\ -20 &-13 \end{array}\right|=4.Matricu Q definirat ćemo kao
Q=\left( \begin{array}{rr} 1 &1 \\\ 1 &0 \end{array} \right).Primijetimo da je determinanta matrice Q jednaka |Q| =-1. Nadalje, vrijedi
Q^{2}= \left( \begin{array}{rr} 1 &1 \\\ 1 &0 \end{array} \right) \left( \begin{array}{rr} 1 &1 \\\ 1 &0 \end{array} \right) = \left( \begin{array}{rr} 2 &1 \\\ 1 &1 \end{array} \right), Q^{3}=\left( \begin{array}{rr} 1 &1 \\\ 1 &0 \end{array} \right) \left( \begin{array}{rr} 2 &1 \\\ 1 &1 \end{array} \right)= \left( \begin{array}{rr} 3 &2 \\\ 2 &1 \end{array} \right), Q^{4}= \left( \begin{array}{rr} 1 &1 \\\ 1 &0 \end{array} \right) \left( \begin{array}{rr} 3 &2 \\\ 2 &1 \end{array} \right)=\left( \begin{array}{rr} 5 &3 \\\ 3 &2 \end{array} \right).Uočimo da se u matricama Q^{2}, Q^{3}, Q^{4} pojavljuju Fibonaccijevi brojevi. Nije teško pretpostaviti kako će izgledati matrica Q^{n}.
Pomoću Teorema
Kombinatorni dokaz i interpretaciju jednakosti (
Neka je m=n. Tada jednakost (
a jednakost (
odnosno
F_{2n}=F_{n}L_{n}.Evo još jedne jednakosti koji povezuje Fibonaccijeve i Lucasove brojeve.
Na kraju dajemo još jednu zanimljivu interpretaciju Fibonaccijevih brojeva pomoću koje se može pokazati Cassinijeva formula (
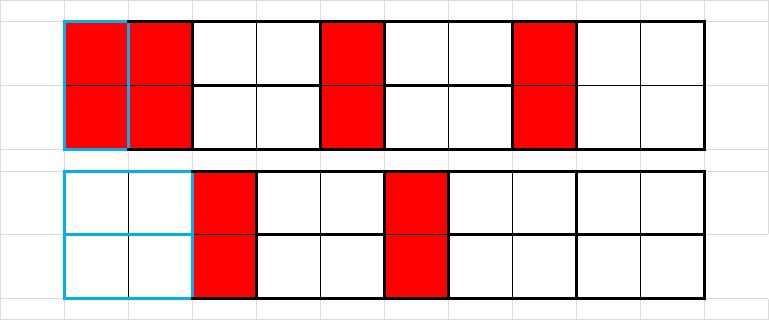
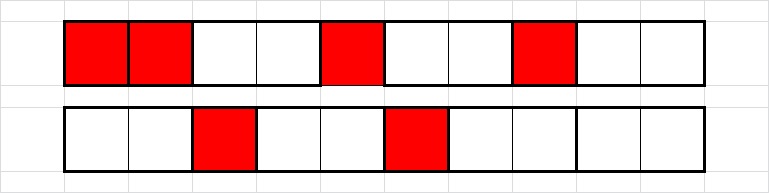
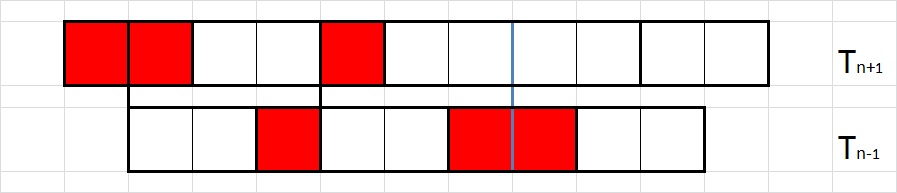
Budući da popločavanje možemo započeti ili s jednom vertikalno postavljenom pločicom ili s dvije horizontalno postavljene (vidi Sliku
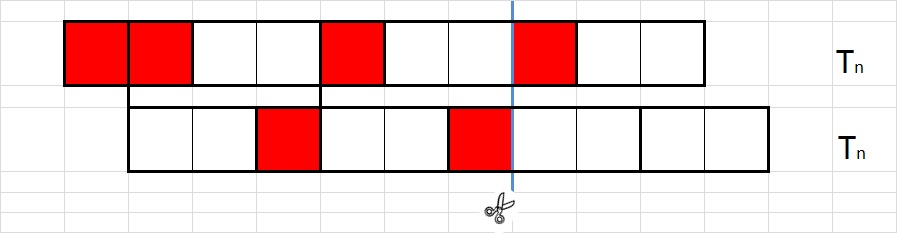
Sada donju ploču pomaknimo za jedno mjesto udesno i pogledajmo na koliko mjesta možemo 'prelomiti' i gornju i donju ploču istovremeno, a da pritom ne lomimo domino pločice. Na primjeru sa Slike
Sada nam preostaje prebrojati načine popločavanja u kojima se ne pojavljuje prijelom. Ukoliko je n paran pojavit će se točno jedno takvo popločavanje dviju ploča iste dimenzije 1\times n, dok svako popločavanje dviju ploča dimenzija 1\times (n+1) i 1\times (n-1) uvijek ima crtu loma jer je broj polja na pločama neparan (pa u popločavanje moramo uključiti pločicu dimenzije 1\times 1). Točno obratno se dešava ako je n neparan (Slika 6, 7). Stoga smo opravdali formulu T_{n}^{2}-T_{n-1}\cdot T_{n+1}=(-1)^{n}, što uz T_{n}=F_{n-1} upravo predstavlja Cassinijevu formulu (
| [1] | B. Bakula, Fibonaccijeve matrice i determinante, diplomski rad, PMF - Matemački odsjek, Sveučilište u Zagrebu, 2013. |
| [2] | A. Dujella, Fibonaccijevi brojevi, HMD, Zagreb, 2000. |
| [3] | T. Koshy, Fibonacci and Lucas numbers with applications, John Wiley \& Sons, 2001. |
| [4] | Cassini's Identity, dostupno na http://www.cut-the-knot.org/arithmetic/algebra/CassinisIdentity.shtml |
| [5] | Fibonacci Tilings, dostupno na http://www.cut-the-knot.org/arithmetic/combinatorics/FibonacciTilings.sh... |