Topološka semantika logika dokazivosti
Modalna logika motivirana je potrebom da se formalizira nužnost i mogućnost, znanje i vjerovanje, dokazivost i mnoga druga svojstva koja se mogu smatrati operatorima na logičkim sudovima.3 Stroga izgradnja logičkog sustava, pa tako i modalne logike, podrazumijeva definiranje sintakse (jezik, izvod, dokaz, teorem) i semantike (model, istinitost, valjanost), te dokazivanje teorema adekvatnosti i potpunosti kao veze sintakse i semantike. U nastavku pretpostavljamo da su ovi pojmovi poznati iz logike sudova i logike prvog reda. Detalji se po potrebi mogu pronaći u svakom početnom udžbeniku matematičke logike, npr.
U ovom članku razmatramo samo propozicionalne modalne logike. Najprije ćemo definirati alfabet osnovne modalne logike.
Alfabet osnovne modalne logike je proširenje alfabeta logike sudova simbolom \Box, tj. skup simbola koji sadrži:
| \bullet | prebrojivo mnogo propozicionalnih varijabli, koje označavamo p,q i sl. |
| \bullet | logičke veznike \neg,\wedge,\vee,\to,\leftrightarrow |
| \bullet | logičke konstante \top,\bot |
| \bullet | \Box, koji zovemo modalni operator. |
Formule modalne logike definiraju se rekurzivno:
| \bullet | propozicionalne varijable i logičke konstante su formule |
| \bullet | ako su A i B formule, onda su \neg A, A\wedge B, A\vee B, A\to B, A\leftrightarrow B, \Box A također formule. |
Definiramo dualni modalni operator \Diamond A kao pokratu za \neg\Box\neg A.
| \bullet | \Box A\to\Box\Box A |
| \bullet | \Diamond A\to\Box\Diamond A |
| \bullet | \Box(A\to B)\to(\Box A\to\Box B) |
Formula oblika \Box(A\to B)\to(\Box A\to\Box B), posljednja navedena u napomeni
Ovisno o intendiranoj interpretaciji, različiti modalni sistemi dobivaju se dodavanjem jednog ili više drugih aksioma, npr. formula \Box A\to A iz napomene
Za modalnu logiku postoji više vrsta semantike (relacijska, topološka, okolinska, algebarska, ... ). U ovom dijelu članka razmatramo relacijsku semantiku, koja se često naziva i Kripkeova semantika ili semantika mogućih svjetova. Kasnije ćemo upoznati i topološku semantiku.
(Kripkeov) model je uređena trojka (W,R,V), gdje je (W,R) okvir, a V valuacija, funkcija koja svakoj propozicionalnoj varijabli p pridružuje podskup nosača V(p)\subseteq W.
Pritom kažemo da je formula p istinita u svijetu w\in W i pišemo w\Vdash p ako je w\in V(p). Definicija istinitosti rekurzivno se proširuje na sve formule:
| \bullet | za svaki svijet w vrijedi w\Vdash\top i w\not\Vdash\bot |
| \bullet | w\Vdash\neg A ako ne vrijedi w\Vdash A |
| \bullet | w\Vdash A\wedge B ako w\Vdash A i w\Vdash B |
| \bullet | w\Vdash\Box A ako za svaki v\in W takav da je wRv vrijedi v\Vdash A. |
Uočimo da iz definicije slijedi da je w\Vdash\Diamond A ako i samo ako postoji v\in W takav da je wRv i v\Vdash A.
Kripkeove modele možemo zamišljati kao jednostavne usmjerene grafove ako svakoj točki grafa (svijetu modela) x pridružimo neki skup propozicionalnih varijabli p za koje vrijedi x \in V(p).
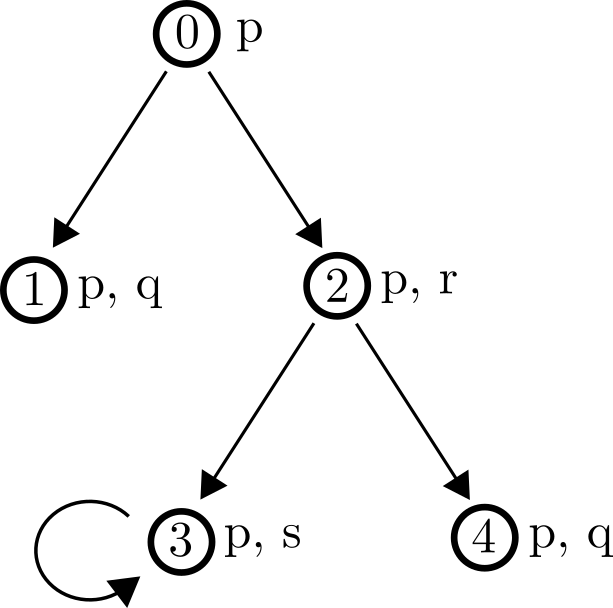
Pogledajmo nekoliko primjera istinitih i neistinitih formula u svijetu 0. Vrijedi li 0 \Vdash \Box p? Da, jer su iz svijeta 0 dostižni samo svjetovi 1 i 2, te u oba vrijedi p. U svijetu 1 nije istinito r, a u svijetu 2 nije istinito q. Stoga ne vrijedi 0 \Vdash \Box r niti 0 \Vdash \Box q. No, primijetimo da vrijedi 0 \Vdash \Diamond q te 0 \Vdash \Diamond r.
Ne vrijedi 0 \Vdash \Diamond s (postoji put, ali ne postoji strelica, iz 0 u 3). Ali, vrijedi 0 \Vdash \Diamond \Diamond s. Zatim, iako ne vrijedi 0 \Vdash \Box q, vrijedi 0 \Vdash \Box (q \vee \Diamond q).
Još neki primjeri formula koje su istinite u 0 su \Box(r \to \Diamond\Diamond\Box s), \Diamond\Diamond\Diamond\Diamond s i \Box(\Diamond q \to \Diamond s). Primijetite petlju na slici. Ona je bitna za istinitost prvih dviju navedenih formula.
Neke formule koje nisu istinite u svijetu 0 su primjerice sljedeće: \Box(\Box q \to q) \to \Box q, \neg q \to \Box \Diamond \neg q i \Diamond \Diamond s \to \Diamond s.
Na internetu postoje stranice na kojima je moguće konstruirati primjere Kripkeovih modela i ispitivati istinitost formula. Jedna takva stranica je na adresi http://rkirsling.github.io/modallogic/.
Sada smo modalnim formulama dali matematičko značenje, pa možemo o ranije spomenutim primjerima formula razmišljati na precizniji način.
Zaista, neka je R refleksivna i w\in W takav da je w\Vdash\Box A. To znači v\Vdash A za sve v takve da je wRv. No zbog refleksivnosti relacije R vrijedi wRw, pa je posebno w\Vdash A. Iz w\Vdash\Box A zaključili smo w\Vdash A, što po semantici logičkog veznika \to povlači w\Vdash\Box A\to A.
Obratno, neka je svaka formula oblika \Box A\to A valjana na okviru (W,R). Pretpostavimo da R nije refleksivna, tj. postoji w\in W takav da ne vrijedi wRw. Neka je V valuacija takva da je V(p)=W\setminus\lbrace w\rbrace. Lako se vidi da tada vrijedi w\Vdash\Box p, ali ne w\Vdash p, dakle u w nije istinita \Box p\to p, što je u kontradikciji s pretpostavkom.
Iz prethodnog primjera slijedi da okviri za epistemičku logiku, u kojoj su formule oblika \Box A\to A aksiomi, nužno imaju refleksivnu relaciju dostiživosti.
| \bullet | \Box A\to \Box\Box A je valjana na (W,R) ako i samo ako je R tranzitivna |
| \bullet | \Diamond A\to\Box\Diamond A je valjana na (W,R) ako i samo ako R ima sljedeće svojstvo: za sve w,v,u\in W, ako je wRv i wRu, onda je vRu |
| \bullet | \Box(A\to B)\to(\Box A\to\Box B) je valjana na svakom okviru. |
Općenito, nužni i dovoljni uvjeti da se neko svojstvo relacije može definirati modalnom formulom dani su poznatim Goldblatt–Thomasonovim teoremom (detalji se mogu vidjeti npr. u knjizi
Za sistem K vrijedi teorem adekvatnosti i potpunosti u odnosu na relacijsku semantiku, tj. za svaku formulu A vrijedi: \vdash A ako i samo ako \Vdash A. Adekvatnost slijedi iz prethodnog zadatka, dok dokaz potpunosti nadilazi okvire ovog članka. Spomenimo, također bez dokaza, da za modalni sistem dobiven dodavanjem aksioma \Box A\to A sistemu K vrijedi adekvatnost i potpunost u odnosu na klasu svih okvira čija je relacija dostižnosti refleksivna. Analogni rezultati vrijede i za ostale spomenute formule, ali i mnoge druge (v. npr.
Sistem GL (Gödel, Löb6) proširenje je osnovnog modalnog sistema K svim formulama oblika \Box(\Box A \to A) \to \Box A kao aksiomima. Shema formula \Box(\Box A \to A) \to \Box A naziva se Löbovim aksiomom i označava s L. Uvodimo oznaku \vdash_{GL}A za modalnu formulu A koja je teorem sistema GL.
Sada ćemo reći nešto o tome što predstavljaju teoremi sistema GL. Radi se o određenoj vezi s Peanovom aritmetikom i drugim formalnim teorijama aritmetike. Peanova aritmetika je jedna teorija prvog reda (v.
Pišemo \vdash_{PA}A ako je A teorem Peanove aritmetike. Predikat dokazivosti Peanove aritmetike je formula Pr(n) čije je neformalno značenje “broj n je kod nekog teorema Peanove aritmetike”.
Prostor nam ne dopušta da pobliže obrazložimo postupak kodiranja koji omogućuje da se dokazivost formula Peanove aritmetike izrazi u samoj Peanovoj aritmetici. Detalji ove konstrukcije mogu se vidjeti u knjizi
Jednom kad smo konstruirali predikat dokazivosti ili se već nekako uvjerili da on postoji, prirodno je pitati se koja su njegova svojstva. Ako je A neka formula Peanove aritmetike, s \ulcorner A \urcorner ćemo označavati njezin kod.
Podsjetimo da je rečenica bilo koja zatvorena formula prvog reda, tj. formula čije su sve varijable u dosegu kvantifikatora. Jedno prirodno pitanje koje bi nas moglo zanimati jest je li formula Pr(\ulcorner A \urcorner) \to A (“ako je A dokaziva, onda vrijedi A”) teorem aritmetike za svaku rečenicu A. Poznati Löbov teorem za Peanovu aritmetiku kaže da je za danu rečenicu A, formula Pr(\ulcorner A \urcorner) \to A dokaziva jedino ako je već i sama formula A dokaziva. Uočimo da to zapravo govori o slabosti Peanove aritmetike. Löbov teorem je tvrdnja koja govori o Peanovoj aritmetici. No, dokaz tvrdnje tog teorema moguće je provesti i unutar same Peanove aritmetike. Pritom je tvrdnja Löbovog teorema formalizirana sljedećom formulom:
Primijetimo da je ova formula sintaktički nalik shemi aksioma L sistema GL.
Sada ćemo precizirati vezu logike dokazivosti i aritmetike.
| \bullet | svakoj propozicionalnoj varijabli p pridružena je proizvoljna rečenica p^{*}; |
| \bullet | funkcija ^{*} komutira s logičkim veznicima (npr. (A \wedge B)^{*} = A^{*} \wedge B^{*}); |
| \bullet | za svaku modalnu formulu A vrijedi (\Box A)^{*} = Pr(\ulcorner A^{*} \urcorner). |
Solovayev8 prvi teorem govori o aritmetičkoj potpunosti sistema GL.
Solovayev teorem nam govori da je, u određenom smislu, sve što Peanova aritmetika može reći o predikatu dokazivosti sadržano u teoriji \textbf{GL}. Vidimo da je njezin aksiom L upravo formalizacija Löbovog teorema. Izrečena veza je vrijedan rezultat jer Peanova aritmetika ima svojstvo neodlučivosti. Neodlučivost teorije je svojstvo da ne postoji algoritam koji će za danu formulu u konačno mnogo koraka ispravno reći je li ona teorem. S druge strane, \textbf{GL} je odlučiva teorija. U idućem ćemo poglavlju napomenuti kako bi izgledao algoritam koji određuje je li dana formula teorem sistema \textbf{GL}. Dakle, kroz sistem \textbf{GL} možemo na jednostavan način, štoviše potpuno mehanički, odgovoriti na preostala pitanja poput ranijeg (negativno odgovorenog) “je li Pr(\ulcorner A \urcorner) \to A teorem aritmetike za svaku rečenicu A?”
Ranije smo spomenuli da za sistem K proširen novom shemom aksioma \Box A \to A vrijede teoremi adekvatnosti i potpunosti u odnosu na klasu svih okvira kod kojih je relacija dostiživosti refleksivna. Sličan rezultat vrijedi za sistem GL.
Dokažite: ako je R tranzitivna i inverzno dobro fundirana, onda je Löbov aksiom valjan na (W,R).
Napominjemo da vrijedi i obrat, koji je nešto teže dokazati, no zainteresiraniji čitatelj može pokušati. No, već i lakši smjer dovoljan je za ključni dio dokaza teorema adekvatnosti za sistem GL, tj. da za svaki formulu A vrijedi: ako je \vdash_{GL}A, onda je A valjana na svakom tranzitivnom i inverzno dobro fundiranom okviru. Vrijedi i obrat, tj. teorem potpunosti, čiji dokaz je, kao što je to i obično slučaj u logici, bitno složeniji. Može se pronaći npr. u knjigama
Primijetimo da su konačna (tranzitivna) stabla poseban slučaj tranzitivnih inverzno dobro fundiranih relacijskih struktura. Stoga je klasa konačnih tranzitivnih stabala adekvatna za GL. No, vrijedi i potpunost.
Ovo je vrlo značajan teorem. Prvo, on se na esencijalan način koristi u Solovayevu teoremu aritmetičke potpunosti. Drugo, on nam daje algoritam provjere je li neka formula A teorem sistema GL. Naprosto simultano prolazimo svim dokazima teorema sustava GL (npr. leksikografski od kraćih ka duljima), i svim konačnim stablima i njihovim valuacijama. Prije ili kasnije će se dogoditi nešto od sljedećeg:
| \bullet | pronaći ćemo dokaz formule A; |
| \bullet | pronaći ćemo model u čijem je nekom svijetu istinita formula A. |
Sada želimo izgraditi još jednu semantiku za sistem GL. Ovoga puta kao temeljnu strukturu ne želimo koristiti okvire već topološke prostore. Naime, u posljednjem dijelu članka promatrat ćemo sistem u kojem nije moguće (na zadovoljavajuć način) definirati relacijsku semantiku, pa moramo posegnuti za topološkom. No, prije toga će nam sistem GL poslužiti kao jednostavniji primjer na kojem ćemo upoznati taj tip semantike. U nastavku pretpostavljamo poznavanje osnovnih pojmova topologije, kao što su topološki prostor, baza, uređajna topologija, gomilište, diskretna topologija i sl. Ako je čitatelju potreban podsjetnik, sve potrebne definicije mogu se pronaći npr. u
Neka je (X,\mathcal{T}) topološki prostor. Na njemu možemo definirati model na posve analogan način kao i na okviru. Ono što trebamo promijeniti je definicija istinitosti za formule oblika \Box A. Naime, u topološkom prostoru više nemamo relaciju dostižnosti.
Istinitost modalnih formula u točki x\in X definira se rekurzivno, pri čemu su slučajevi propozicionalnih varijabli, logičkih konstanti i formula dobivenih primjenom logičkih veznika isti kao kod relacijske semantike, te se definira x\Vdash\Box A ako postoji U\in\mathcal{T} takav da je x\in U i za sve y\in U takve da je y\neq x vrijedi y\Vdash A.
Kažemo da je formula valjana na topološkom prostoru (X,\mathcal{T}) ako je istinita u svakoj točki svakog topološkog modela (X,\mathcal{T}, V).
Uočimo da je x\Vdash\Diamond A ako i samo ako za svaki U\in\mathcal{T} takav da je x\in U postoji y\in U takav da je y\neq x i y\Vdash A. Drugim riječima, x\Vdash\Diamond A ekvivalentno je s činjenicom da je x gomilište skupa \lbrace y\in X:y\Vdash A\rbrace.
Kažemo da je topološki prostor (X,\mathcal{T}) raspršen ako svaki neprazan podskup S\subseteq X ima izoliranu točku, tj. postoji točka s \in S i neka njena okolina O\in\mathcal{T} tako da vrijedi S \cap O = \lbrace s \rbrace.
Propozicija se dokazuje raspisivanjem definicija, na sličan način kao
Adekvatnost i potpunost sistema GL u odnosu na klasu svih raspršenih topoloških prostora dokazao je Esakia9 1981. Iako je sam teorem dobro poznat, njegov dokaz je, koliko nam je poznato, objavljen samo u publikaciji
Uvedimo jednu oznaku. Neka je dan okvir (X, R). Za točku x \in X označimo s R[x] skup \lbrace y \in X \ | \ xRy \rbrace.
Prethodna propozicija ima jednostavan dokaz (v.
U dokazu idućeg teorema ćemo s \Vdash_{R} označavati istinitost u Kripkeovom modelu, a s \Vdash_{T} istinitost u topološkom modelu.
Neka je topologija \mathcal{T} generirana familijom B sljedećeg oblika:
Promotrimo topološki model (W, \mathcal{T},V) s istim nosačem i valuacijom kao (W,R,V). Dokažimo da za sve formule G i točke x \in W vrijedi:
Neka vrijedi x \Vdash_{R} G. Dakle, za sve točke y \in R[x] vrijedi y \Vdash_{R} H. Kako je H manje složenosti od G, po pretpostavci indukcije za sve točke y \in R[x] vrijedi y \Vdash_{T} H. Kratko pišemo R[x] \Vdash_{T} H. No iz definicije baze B slijedi da je \lbrace x\rbrace \cup R[x] okolina točke x, pa po definiciji istinitosti u točki topološkog modela slijedi x \Vdash_{T} G. Slično se dokazuje i obrat.
Sada iz ranije dokazane činjenice w\nVdash_{R} F i upravo dokazane tvrdnje slijedi w \nVdash_{T} F.
Teoremi adekvatnosti i potpunosti za GL u odnosu na topološku semantiku ponekad se formuliraju tako da se kaže da je “GL logika raspršenih prostora”. Semantike modalnih logika nam olakšavaju analizu njihovih svojstava. Primjerice, puno je lakše semantički argumentirati da neka formula nije teorem dane modalne logike. No veza je dvosmjerna. Primjerice, dobro je poznato da su formule oblika \Diamond \Diamond A \to \Diamond A teoremi sustava GL. No iz činjenice da je “GL logika raspršenih prostora” odmah slijedi da je za svaki raspršen prostor (X, \mathcal{T}) i njegov podskup S \subseteq X, skup gomilišta skupa gomilišta od S podskup skupa gomilišta od S.
Vidjeli smo vezu između GL i raspršenih prostora. No, vidjeli smo i da za GL imamo jednostavnu relacijsku semantiku. Važnost se topološkog pristupa vidi tek u proširenjima sistema GL.
Sistem GLP uveo je Japaridze10 1986. Radi se o proširenju sistema GL s prebrojivo mnogo modalnih operatora [n] indeksiranih prirodnim brojevima.11 Formule sistema GLP se definiraju rekurzivno, slično kao formule sistema GL. Naglasimo samo dio definicije koji se odnosi na nove modalne operatore: ako je A formula, onda je i [n]A formula (za sve prirodne brojeve n). Slično kao ranije, koristimo pokratu {\left\lt n\right\gt }A za \neg[n]\neg A.
Aksiomi su sve tautologije (u novom jeziku!), te sheme aksioma:
| \bullet | (K_{n})[n](A\to B)\to([n]A\to[n]B) |
| \bullet | (L_{n})[n]([n]A\to A)\to[n]A |
| \bullet | (P_{n}^{m})[n]A\to[m]A, ako je n\lt m |
| \bullet | (Q_{n}^{m}){\left\lt n\right\gt }A\to[m]{\left\lt n\right\gt }A, ako je n\lt m |
Uočimo da prve dvije sheme aksioma sugeriraju da se radi o nizu operatora dokazivosti, dok druge dvije određuju odnos među njima. Pravila izvoda su modus ponens i \displaystyle{\frac{A}{[n]A}}, n\in\mathbb{N}.
Aritmetička interpretacija sistema GLP je svaka funkcija * sa skupa svih formula sistema GLP u skup rečenica Peanove aritmetike sa svojstvima analognim aritmetičkoj interpretaciji sistema GL, pri čemu je [0] interpretiran kao \Box, tj. ([0]A)^{*} = Pr(\ulcorner A^{*}\urcorner), te je ([n]A)^{*} definirana tako da, neformalno govoreći, ima značenje “A^{*} je dokaziva u teoriji proširenoj svim istinitim \Pi_{n} rečenicama”, gdje su \Pi_{n} rečenice one koje sadrže kvantifikatore samo na početku formule i imaju n alternacija kvantifikatora od kojih je prvi \forall. Potrebno je dokazati da je ovako definirani niz predikata dokazivosti moguće formalizirati koristeći kodiranje, no ovdje nećemo ulaziti u detalje.
Aritmetičku adekvatnost i potpunost dokazao je Japaridze u radu
Okvir za polimodalnu logiku je relacijska struktura s nosačem W\neq\emptyset i indeksiranom familijom relacija dostižnosti pridruženih modalnim operatorima. Istinitost formula definira se za svaki modalni operator analogno kao za \Box u slučaju osnovnog modalnog jezika. Dakle, u slučaju sistema GLP okvir bi bio (W,(R_{n})_{n\in\mathbb{N}}), R_{n}\subseteq W\times W, n\in\mathbb{N}, a iz definicije istinitosti istaknimo samo da se definira w\Vdash[n]A ako za sve u takve da je wR_{n}u vrijedi u\Vdash A.
Analogno sistemu GL, [n]([n]A\to A)\to[n]A je valjana ako i samo ako je R_{n} tranzitivna i inverzno dobro fundirana.
| \bullet | [n]A\to[n+1]A je valjana na okviru (W,(R_{n})_{n\in\mathbb{N}}) ako i samo ako R_{n+1}\subseteq R_{n} |
| \bullet | {\left\lt n\right\gt }A\to[n+1]{\left\lt n\right\gt }A je valjana na okviru (W,(R_{n})_{n\in\mathbb{N}}) ako i samo ako wR_{n}v i wR_{n+1}u povlači uR_{n}v. |
Dakle, postoji samo trivijalna relacijska semantika za GLP. Stoga koristimo topološku semantiku.
Neka je X\neq\emptyset i (X,\mathcal{T}_{n}) topološki prostor, za svaki n\in\mathbb{N}. Uređeni par (X,(\mathcal{T}_{n})_{n\in\mathbb{N}}) zvat ćemo politopološki prostor. Za S\subseteq X, s dS standardno se označava skup gomilišta skupa S. U politopološkom prostoru ćemo s d_{n}S označavati skup gomilišta skupa S s obzirom na topologiju \mathcal{T}_{n}.
Kažemo da je formula valjana na politopološkom prostoru (X,(\mathcal{T}_{n})_{n\in\mathbb{N}}) ako je istinita u svakoj točki svakog politopološkog modela (X,(\mathcal{T}_{n})_{n\in\mathbb{N}},V).
Uočimo da vrijedi x\Vdash{\left\lt n\right\gt }A ako i samo ako je x\in d_{n}\lbrace y\in X:y\Vdash A\rbrace.
Istaknimo teorem adekvatnosti topološke semantike za GLP.
| (1) | (X,\mathcal{T}_{n}) je raspršen topološki prostor |
| (2) | \mathcal{T}_{n}\subseteq\mathcal{T}_{n+1} (tj. \mathcal{T}_{n+1} je finija topologija od \mathcal{T}_{n}) |
| (3) | za svaki S\subseteq X vrijedi d_{n}S\in\mathcal{T}_{n+1} |
Dokaz ovog teorema prepuštamo čitatelju (detalji se mogu pronaći i u radu
Politopološke prostore za koje vrijede pretpostavke prethodnog teorema zovemo GLP-prostori. Potpunost sistema GLP u odnosu na GLP-prostore dokazana je u članku
| [1] | L. Beklemishev, D. Gabelaia: Topological completeness of provability logic GLP, Annals of Pure and Applied Logic 164 (2013) 1201–1223. |
| [2] | P. Blackburn, M. de Rijke, Y. Venema: Modal Logic, Cambridge University Press, 2001. |
| [3] | G. Boolos: The Logic of Provability, Cambridge University Press, 1995. |
| [4] | L. Esakia: Dijagonalne konstrukcije, Löbova formula i Cantorovi raspršeni prostori, u: Istraživanja u logici i semantici, str. 128–-143, Metsniereba, Tbilisi 1981. (na ruskom jeziku) |
| [5] | G. Japaridze: Polimodalna logika dokazivosti, u: Intenzionalne logike i logička sturktura teorija, str. 16–48, Metsniereba, Tbilisi 1988. (na ruskom jeziku) |
| [6] | J. Garson: Modal logic, u: E. N. Zalta (ur.) The Stanford Encyclopedia of Philosophy, Stanford University, 2016. (pristupljeno 16. 2. 2017. na https://plato.stanford.edu/entries/logic-modal/) |
| [7] | I. Gavran, M. Vuković: Logička analiza hibridnih sustava, Poučak 58 (2014) 4–16. |
| [8] | L. Mikec: Topološka potpunost logika dokazivosti (diplomski rad), Prirodoslovno-matematički fakultet – Matematički odsjek, 2016. (pristupljeno 16. 2. 2017. na https://www.math.pmf.unizg.hr/sites/default/files/pictures/mikec-toplosk...) |
| [9] | P. Smith: An Introduction to G"odel's Theorems, Cambridge University Press, 2007. |
| [10] | C. Smorynski: Self–Reference and Modal Logic, Springer, 1985. |
| [11] | Š. Ungar: Opća topologija (materijali za kolegij), Zagreb 2012. (pristupljeno 16. 2. 2017. na https://web.math.pmf.unizg.hr/~ungar/NASTAVA/OT/) |
| [12] |
M. Vuković: Matematička logika, Element, Zagreb 2009. |